One-Step Residual Shifting Diffusion for Image Super-Resolution via Distillation

Diffusion models for super-resolution (SR) produce high-quality visual results but require expensive computational costs. Despite the development of several methods to accelerate diffusion-based SR models, some (e.g., SinSR) fail to produce realistic perceptual details, while others (e.g., OSEDiff) may hallucinate non-existent structures. To overcome these issues, we present RSD, a new distillation method for ResShift, one of the top diffusion-based SR models. Our method is based on training the student network to produce such images that a new fake ResShift model trained on them will coincide with the teacher model. RSD achieves single-step restoration and outperforms the teacher by a large margin. We show that our distillation method can surpass the other distillation-based method for ResShift - SinSR - making it on par with state-of-the-art diffusion-based SR distillation methods. Compared to SR methods based on pre-trained text-to-image models, RSD produces competitive perceptual quality, provides images with better alignment to degraded input images, and requires fewer parameters and GPU memory. We provide experimental results on various real-world and synthetic datasets, including RealSR, RealSet65, DRealSR, ImageNet, and DIV2K.

Field Matching: an Electrostatic Paradigm to Generate and Transfer Data

We propose Electrostatic Field Matching (EFM), a novel method that is suitable for both generative modeling and distribution transfer tasks. Our approach is inspired by the physics of an electrical capacitor. We place source and target distributions on the capacitor plates and assign them positive and negative charges, respectively. We then learn the electrostatic field of the capacitor using a neural network approximator. To map the distributions to each other, we start at one plate of the capacitor and move the samples along the learned electrostatic field lines until they reach the other plate. We theoretically justify that this approach provably yields the distribution transfer. In practice, we demonstrate the performance of our EFM in toy and image data experiments.

InfoBridge: Mutual Information estimation via Bridge Matching

Diffusion bridge models have recently become a powerful tool in the field of generative modeling. In this work, we leverage their power to address another important problem in machine learning and information theory - the estimation of the mutual information (MI) between two random variables. We show that by using the theory of diffusion bridges, one can construct an unbiased estimator for data posing difficulties for conventional MI estimators. We showcase the performance of our estimator on a series of standard MI estimation benchmarks.

Categorical Schrödinger Bridge Matching

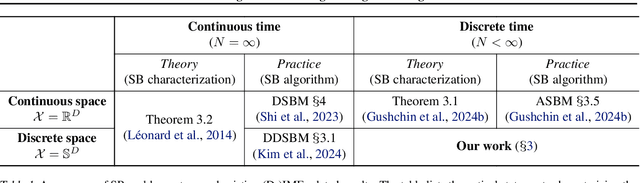
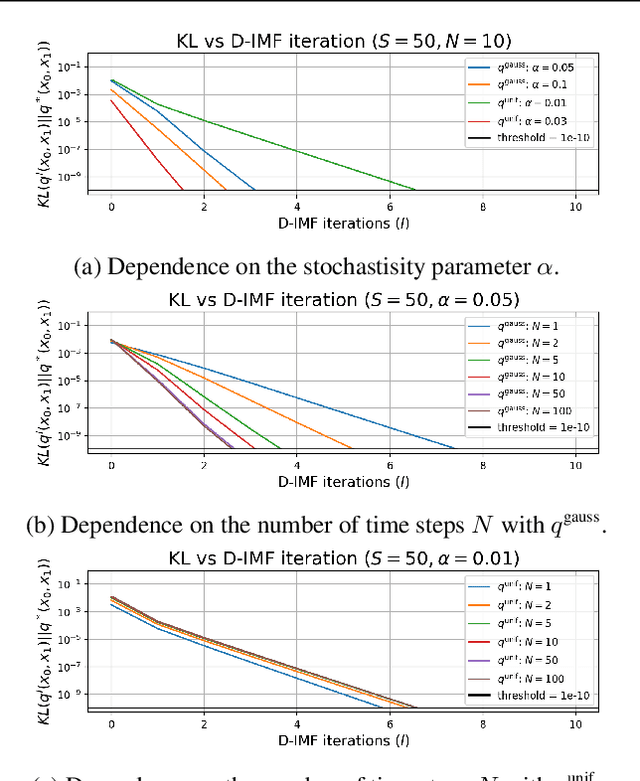
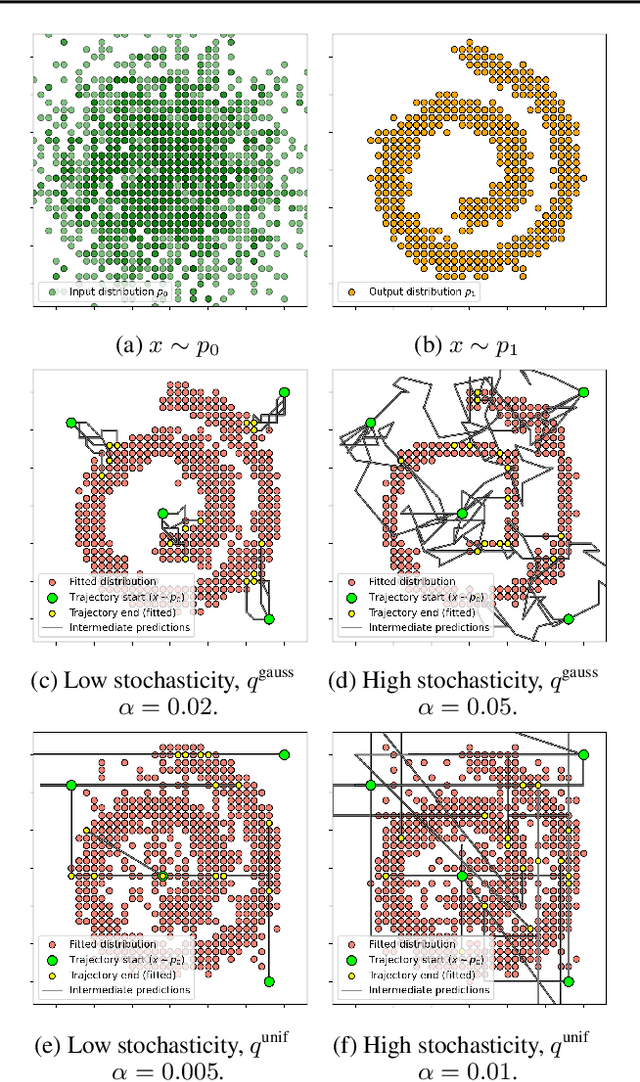
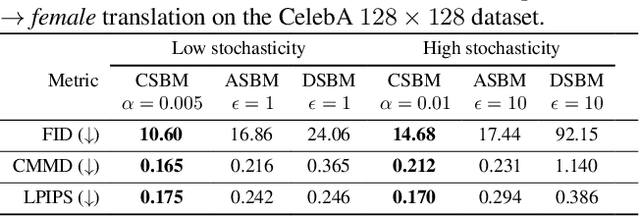
The Schr\"odinger Bridge (SB) is a powerful framework for solving generative modeling tasks such as unpaired domain translation. Most SB-related research focuses on continuous data space $\mathbb{R}^{D}$ and leaves open theoretical and algorithmic questions about applying SB methods to discrete data, e.g, on finite spaces $\mathbb{S}^{D}$. Notable examples of such sets $\mathbb{S}$ are codebooks of vector-quantized (VQ) representations of modern autoencoders, tokens in texts, categories of atoms in molecules, etc. In this paper, we provide a theoretical and algorithmic foundation for solving SB in discrete spaces using the recently introduced Iterative Markovian Fitting (IMF) procedure. Specifically, we theoretically justify the convergence of discrete-time IMF (D-IMF) to SB in discrete spaces. This enables us to develop a practical computational algorithm for SB which we call Categorical Schr\"odinger Bridge Matching (CSBM). We show the performance of CSBM via a series of experiments with synthetic data and VQ representations of images.

Inverse Bridge Matching Distillation

Learning diffusion bridge models is easy; making them fast and practical is an art. Diffusion bridge models (DBMs) are a promising extension of diffusion models for applications in image-to-image translation. However, like many modern diffusion and flow models, DBMs suffer from the problem of slow inference. To address it, we propose a novel distillation technique based on the inverse bridge matching formulation and derive the tractable objective to solve it in practice. Unlike previously developed DBM distillation techniques, the proposed method can distill both conditional and unconditional types of DBMs, distill models in a one-step generator, and use only the corrupted images for training. We evaluate our approach for both conditional and unconditional types of bridge matching on a wide set of setups, including super-resolution, JPEG restoration, sketch-to-image, and other tasks, and show that our distillation technique allows us to accelerate the inference of DBMs from 4x to 100x and even provide better generation quality than used teacher model depending on particular setup.

A Statistical Learning Perspective on Semi-dual Adversarial Neural Optimal Transport Solvers

Neural network based Optimal Transport (OT) is a recent and fruitful direction in the generative modeling community. It finds its applications in various fields such as domain translation, image super-resolution, computational biology and others. Among the existing approaches to OT, of considerable interest are adversarial minimax solvers based on semi-dual formulations of OT problems. While promising, these methods lack theoretical investigation from a statistical learning perspective. Our work fills this gap by establishing upper bounds on the generalization error of an approximate OT map recovered by the minimax quadratic OT solver. Importantly, the bounds we derive depend solely on some standard statistical and mathematical properties of the considered functional classes (neural networks). While our analysis focuses on the quadratic OT, we believe that similar bounds could be derived for more general OT formulations, paving the promising direction for future research.

Online Algorithm for Aggregating Experts' Predictions with Unbounded Quadratic Loss

We consider the problem of online aggregation of expert predictions with the quadratic loss function. We propose an algorithm for aggregating expert predictions which does not require a prior knowledge of the upper bound on the losses. The algorithm is based on the exponential reweighing of expert losses.

Rethinking Optimal Transport in Offline Reinforcement Learning

We propose a novel algorithm for offline reinforcement learning using optimal transport. Typically, in offline reinforcement learning, the data is provided by various experts and some of them can be sub-optimal. To extract an efficient policy, it is necessary to \emph{stitch} the best behaviors from the dataset. To address this problem, we rethink offline reinforcement learning as an optimal transportation problem. And based on this, we present an algorithm that aims to find a policy that maps states to a \emph{partial} distribution of the best expert actions for each given state. We evaluate the performance of our algorithm on continuous control problems from the D4RL suite and demonstrate improvements over existing methods.

Robust Barycenter Estimation using Semi-Unbalanced Neural Optimal Transport

A common challenge in aggregating data from multiple sources can be formalized as an \textit{Optimal Transport} (OT) barycenter problem, which seeks to compute the average of probability distributions with respect to OT discrepancies. However, the presence of outliers and noise in the data measures can significantly hinder the performance of traditional statistical methods for estimating OT barycenters. To address this issue, we propose a novel, scalable approach for estimating the \textit{robust} continuous barycenter, leveraging the dual formulation of the \textit{(semi-)unbalanced} OT problem. To the best of our knowledge, this paper is the first attempt to develop an algorithm for robust barycenters under the continuous distribution setup. Our method is framed as a $\min$-$\max$ optimization problem and is adaptable to \textit{general} cost function. We rigorously establish the theoretical underpinnings of the proposed method and demonstrate its robustness to outliers and class imbalance through a number of illustrative experiments.

Diffusion & Adversarial Schrödinger Bridges via Iterative Proportional Markovian Fitting

The Iterative Markovian Fitting (IMF) procedure based on iterative reciprocal and Markovian projections has recently been proposed as a powerful method for solving the Schr\"odinger Bridge problem. However, it has been observed that for the practical implementation of this procedure, it is crucial to alternate between fitting a forward and backward time diffusion at each iteration. Such implementation is thought to be a practical heuristic, which is required to stabilize training and obtain good results in applications such as unpaired domain translation. In our work, we show that this heuristic closely connects with the pioneer approaches for the Schr\"odinger Bridge based on the Iterative Proportional Fitting (IPF) procedure. Namely, we find that the practical implementation of IMF is, in fact, a combination of IMF and IPF procedures, and we call this combination the Iterative Proportional Markovian Fitting (IPMF) procedure. We show both theoretically and practically that this combined IPMF procedure can converge under more general settings, thus, showing that the IPMF procedure opens a door towards developing a unified framework for solving Schr\"odinger Bridge problems.