Towards Diverse and Comprehensive Benchmarks for Mutual Information Estimation

Mutual information (MI) estimation is a central problem in machine learning and statistics; however, existing benchmarks typically evaluate estimators on simplified, low-dimensional distributions, leaving their performance on complex, realistic data largely unexplored. We address this gap with a comprehensive benchmarking framework grounded in a unified copula-theoretic perspective that subsumes existing benchmarks as special cases. Within this framework, we propose two complementary families of tests: a copula-first family that systematically varies ground-truth MI, dimensionality, and marginal complexity using synthetic and flow-based transformations; and a marginals-first family that couples real-world image data with controlled dependency structures, extending the classic same-class-pairing paradigm. We use this suite to extensively evaluate three classes of estimators: non-parametric, discriminative, and generative. Contrary to prevailing assumptions, our results indicate that there is no universal winner: each category can systematically outperform all other estimators under specific setups. By analyzing these cases, we identify fundamental estimation barriers and propose new tests that more effectively stress these specific limitations. We share the open source code at https://github.com/VanessB/mutinfo.

Discrete Bridges for Mutual Information Estimation

Diffusion bridge models in both continuous and discrete state spaces have recently become powerful tools in the field of generative modeling. In this work, we leverage the discrete state space formulation of bridge matching models to address another important problem in machine learning and information theory: the estimation of the mutual information (MI) between discrete random variables. By neatly framing MI estimation as a domain transfer problem, we construct a Discrete Bridge Mutual Information (DBMI) estimator suitable for discrete data, which poses difficulties for conventional MI estimators. We showcase the performance of our estimator on two MI estimation settings: low-dimensional and image-based.

FMMI: Flow Matching Mutual Information Estimation

We introduce a novel Mutual Information (MI) estimator that fundamentally reframes the discriminative approach. Instead of training a classifier to discriminate between joint and marginal distributions, we learn a normalizing flow that transforms one into the other. This technique produces a computationally efficient and precise MI estimate that scales well to high dimensions and across a wide range of ground-truth MI values.

Curse of Slicing: Why Sliced Mutual Information is a Deceptive Measure of Statistical Dependence

Sliced Mutual Information (SMI) is widely used as a scalable alternative to mutual information for measuring non-linear statistical dependence. Despite its advantages, such as faster convergence, robustness to high dimensionality, and nullification only under statistical independence, we demonstrate that SMI is highly susceptible to data manipulation and exhibits counterintuitive behavior. Through extensive benchmarking and theoretical analysis, we show that SMI saturates easily, fails to detect increases in statistical dependence (even under linear transformations designed to enhance the extraction of information), prioritizes redundancy over informative content, and in some cases, performs worse than simpler dependence measures like the correlation coefficient.

InfoBridge: Mutual Information estimation via Bridge Matching

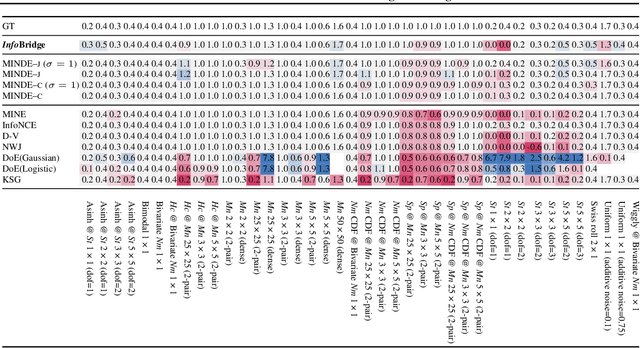
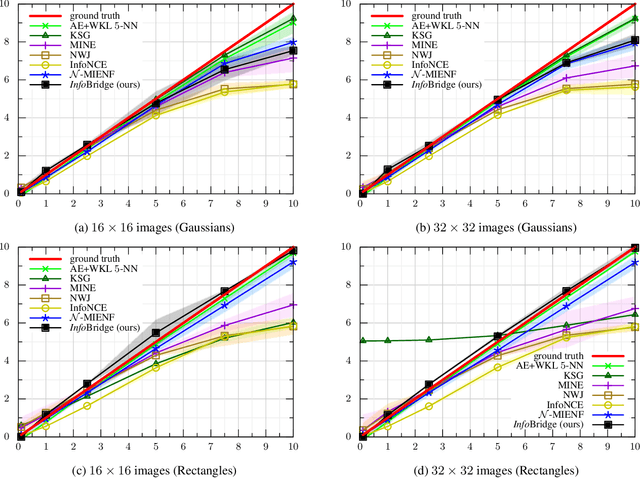
Diffusion bridge models have recently become a powerful tool in the field of generative modeling. In this work, we leverage their power to address another important problem in machine learning and information theory - the estimation of the mutual information (MI) between two random variables. We show that by using the theory of diffusion bridges, one can construct an unbiased estimator for data posing difficulties for conventional MI estimators. We showcase the performance of our estimator on a series of standard MI estimation benchmarks.

Efficient Distribution Matching of Representations via Noise-Injected Deep InfoMax

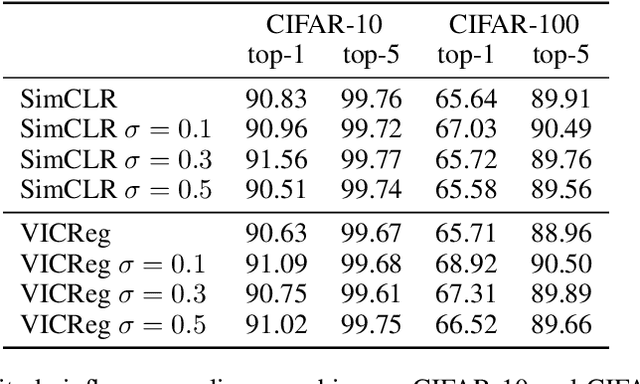
Deep InfoMax (DIM) is a well-established method for self-supervised representation learning (SSRL) based on maximization of the mutual information between the input and the output of a deep neural network encoder. Despite the DIM and contrastive SSRL in general being well-explored, the task of learning representations conforming to a specific distribution (i.e., distribution matching, DM) is still under-addressed. Motivated by the importance of DM to several downstream tasks (including generative modeling, disentanglement, outliers detection and other), we enhance DIM to enable automatic matching of learned representations to a selected prior distribution. To achieve this, we propose injecting an independent noise into the normalized outputs of the encoder, while keeping the same InfoMax training objective. We show that such modification allows for learning uniformly and normally distributed representations, as well as representations of other absolutely continuous distributions. Our approach is tested on various downstream tasks. The results indicate a moderate trade-off between the performance on the downstream tasks and quality of DM.

Mutual Information Estimation via Normalizing Flows

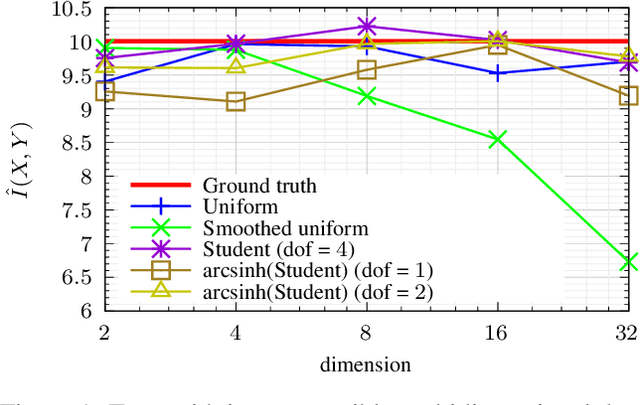
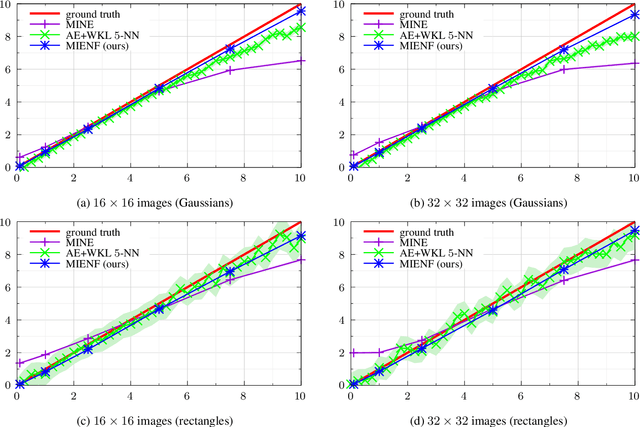
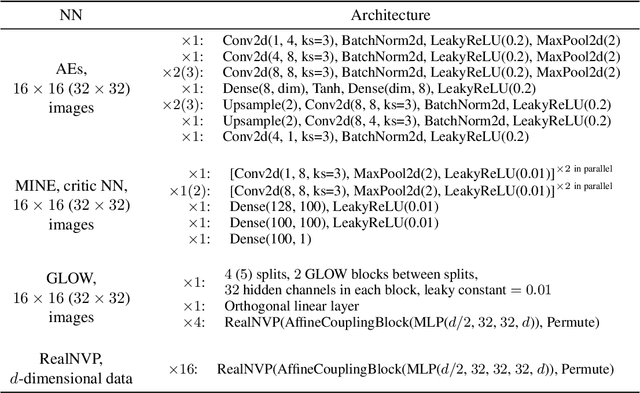
We propose a novel approach to the problem of mutual information (MI) estimation via introducing normalizing flows-based estimator. The estimator maps original data to the target distribution with known closed-form expression for MI. We demonstrate that our approach yields MI estimates for the original data. Experiments with high-dimensional data are provided to show the advantages of the proposed estimator.

Information Bottleneck Analysis of Deep Neural Networks via Lossy Compression

The Information Bottleneck (IB) principle offers an information-theoretic framework for analyzing the training process of deep neural networks (DNNs). Its essence lies in tracking the dynamics of two mutual information (MI) values: one between the hidden layer and the class label, and the other between the hidden layer and the DNN input. According to the hypothesis put forth by Shwartz-Ziv and Tishby (2017), the training process consists of two distinct phases: fitting and compression. The latter phase is believed to account for the good generalization performance exhibited by DNNs. Due to the challenging nature of estimating MI between high-dimensional random vectors, this hypothesis has only been verified for toy NNs or specific types of NNs, such as quantized NNs and dropout NNs. In this paper, we introduce a comprehensive framework for conducting IB analysis of general NNs. Our approach leverages the stochastic NN method proposed by Goldfeld et al. (2019) and incorporates a compression step to overcome the obstacles associated with high dimensionality. In other words, we estimate the MI between the compressed representations of high-dimensional random vectors. The proposed method is supported by both theoretical and practical justifications. Notably, we demonstrate the accuracy of our estimator through synthetic experiments featuring predefined MI values. Finally, we perform IB analysis on a close-to-real-scale convolutional DNN, which reveals new features of the MI dynamics.