On lower bounds of the density of planar periodic sets without unit distances

Determining the maximal density $m_1(\mathbb{R}^2)$ of planar sets without unit distances is a fundamental problem in combinatorial geometry. This paper investigates lower bounds for this quantity. We introduce a novel approach to estimating $m_1(\mathbb{R}^2)$ by reformulating the problem as a Maximal Independent Set (MIS) problem on graphs constructed from flat torus, focusing on periodic sets with respect to two non-collinear vectors. Our experimental results supported by theoretical justifications of proposed method demonstrate that for a sufficiently wide range of parameters this approach does not improve the known lower bound $0.22936 \le m_1(\mathbb{R}^2)$. The best discrete sets found are approximations of Croft's construction. In addition, several open source software packages for MIS problem are compared on this task.

Efficient Distribution Matching of Representations via Noise-Injected Deep InfoMax

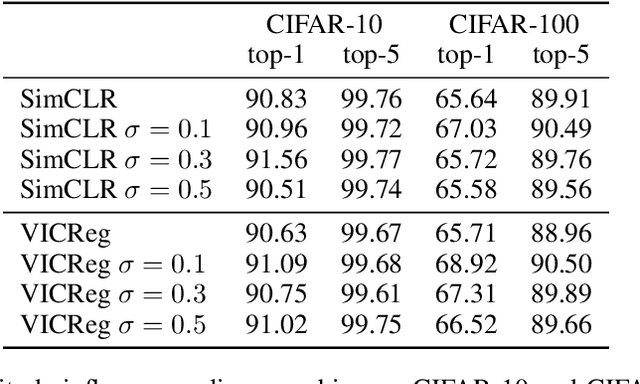
Deep InfoMax (DIM) is a well-established method for self-supervised representation learning (SSRL) based on maximization of the mutual information between the input and the output of a deep neural network encoder. Despite the DIM and contrastive SSRL in general being well-explored, the task of learning representations conforming to a specific distribution (i.e., distribution matching, DM) is still under-addressed. Motivated by the importance of DM to several downstream tasks (including generative modeling, disentanglement, outliers detection and other), we enhance DIM to enable automatic matching of learned representations to a selected prior distribution. To achieve this, we propose injecting an independent noise into the normalized outputs of the encoder, while keeping the same InfoMax training objective. We show that such modification allows for learning uniformly and normally distributed representations, as well as representations of other absolutely continuous distributions. Our approach is tested on various downstream tasks. The results indicate a moderate trade-off between the performance on the downstream tasks and quality of DM.

Mutual Information Estimation via Normalizing Flows

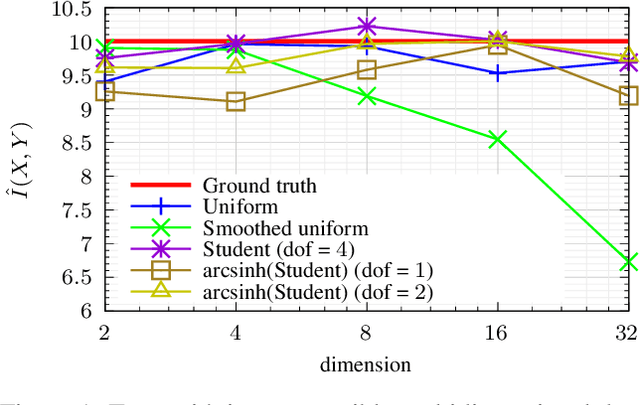
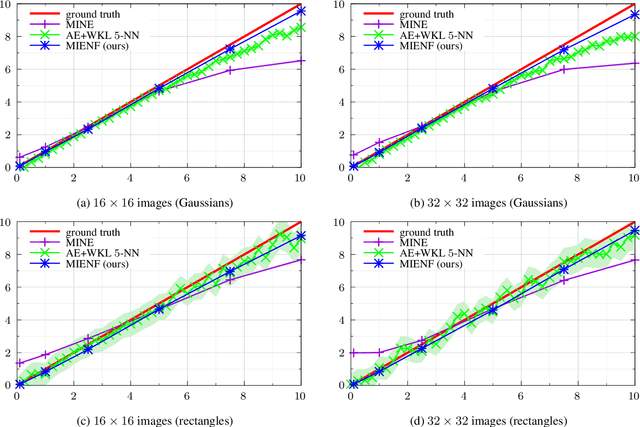
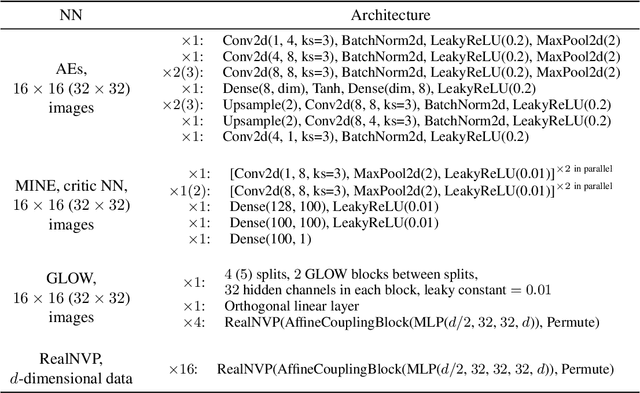
We propose a novel approach to the problem of mutual information (MI) estimation via introducing normalizing flows-based estimator. The estimator maps original data to the target distribution with known closed-form expression for MI. We demonstrate that our approach yields MI estimates for the original data. Experiments with high-dimensional data are provided to show the advantages of the proposed estimator.