Efficient Distribution Matching of Representations via Noise-Injected Deep InfoMax

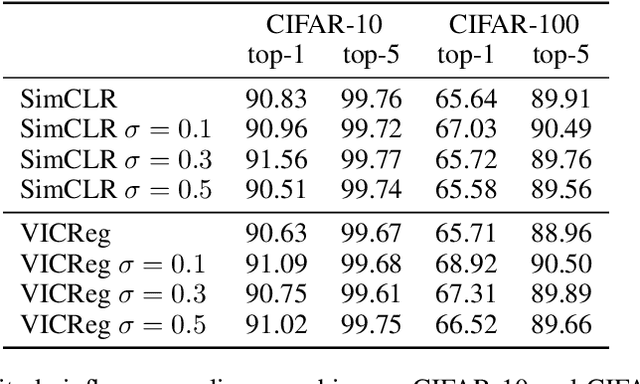
Deep InfoMax (DIM) is a well-established method for self-supervised representation learning (SSRL) based on maximization of the mutual information between the input and the output of a deep neural network encoder. Despite the DIM and contrastive SSRL in general being well-explored, the task of learning representations conforming to a specific distribution (i.e., distribution matching, DM) is still under-addressed. Motivated by the importance of DM to several downstream tasks (including generative modeling, disentanglement, outliers detection and other), we enhance DIM to enable automatic matching of learned representations to a selected prior distribution. To achieve this, we propose injecting an independent noise into the normalized outputs of the encoder, while keeping the same InfoMax training objective. We show that such modification allows for learning uniformly and normally distributed representations, as well as representations of other absolutely continuous distributions. Our approach is tested on various downstream tasks. The results indicate a moderate trade-off between the performance on the downstream tasks and quality of DM.

Bridging Spectral Embedding and Matrix Completion in Self-Supervised Learning

Self-supervised methods received tremendous attention thanks to their seemingly heuristic approach to learning representations that respect the semantics of the data without any apparent supervision in the form of labels. A growing body of literature is already being published in an attempt to build a coherent and theoretically grounded understanding of the workings of a zoo of losses used in modern self-supervised representation learning methods. In this paper, we attempt to provide an understanding from the perspective of a Laplace operator and connect the inductive bias stemming from the augmentation process to a low-rank matrix completion problem. To this end, we leverage the results from low-rank matrix completion to provide theoretical analysis on the convergence of modern SSL methods and a key property that affects their downstream performance.

Unsupervised Embedding Quality Evaluation

Unsupervised learning has recently significantly gained in popularity, especially with deep learning-based approaches. Despite numerous successes and approaching supervised-level performance on a variety of academic benchmarks, it is still hard to train and evaluate SSL models in practice due to the unsupervised nature of the problem. Even with networks trained in a supervised fashion, it is often unclear whether they will perform well when transferred to another domain. Past works are generally limited to assessing the amount of information contained in embeddings, which is most relevant for self-supervised learning of deep neural networks. This works chooses to follow a different approach: can we quantify how easy it is to linearly separate the data in a stable way? We survey the literature and uncover three methods that could be potentially used for evaluating quality of representations. We also introduce one novel method based on recent advances in understanding the high-dimensional geometric structure self-supervised learning. We conduct extensive experiments and study the properties of these metrics and ones introduced in the previous work. Our results suggest that while there is no free lunch, there are metrics that can robustly estimate embedding quality in an unsupervised way.

CC-Cert: A Probabilistic Approach to Certify General Robustness of Neural Networks

In safety-critical machine learning applications, it is crucial to defend models against adversarial attacks -- small modifications of the input that change the predictions. Besides rigorously studied $\ell_p$-bounded additive perturbations, recently proposed semantic perturbations (e.g. rotation, translation) raise a serious concern on deploying ML systems in real-world. Therefore, it is important to provide provable guarantees for deep learning models against semantically meaningful input transformations. In this paper, we propose a new universal probabilistic certification approach based on Chernoff-Cramer bounds that can be used in general attack settings. We estimate the probability of a model to fail if the attack is sampled from a certain distribution. Our theoretical findings are supported by experimental results on different datasets.

GRASP: Graph Alignment through Spectral Signatures

What is the best way to match the nodes of two graphs? This graph alignment problem generalizes graph isomorphism and arises in applications from social network analysis to bioinformatics. Some solutions assume that auxiliary information on known matches or node or edge attributes is available, or utilize arbitrary graph features. Such methods fare poorly in the pure form of the problem, in which only graph structures are given. Other proposals translate the problem to one of aligning node embeddings, yet, by doing so, provide only a single-scale view of the graph. In this paper, we transfer the shape-analysis concept of functional maps from the continuous to the discrete case, and treat the graph alignment problem as a special case of the problem of finding a mapping between functions on graphs. We present GRASP, a method that first establishes a correspondence between functions derived from Laplacian matrix eigenvectors, which capture multiscale structural characteristics, and then exploits this correspondence to align nodes. Our experimental study, featuring noise levels higher than anything used in previous studies, shows that GRASP outperforms state-of-the-art methods for graph alignment across noise levels and graph types.

FREDE: Linear-Space Anytime Graph Embeddings

Low-dimensional representations, or embeddings, of a graph's nodes facilitate data mining tasks. Known embedding methods explicitly or implicitly rely on a similarity measure among nodes. As the similarity matrix is quadratic, a tradeoff between space complexity and embedding quality arises; past research initially opted for heuristics and linear-transform factorizations, which allow for linear space but compromise on quality; recent research has proposed a quadratic-space solution as a viable option too. In this paper we observe that embedding methods effectively aim to preserve the covariance among the rows of a similarity matrix, and raise the question: is there a method that combines (i) linear space complexity, (ii) a nonlinear transform as its basis, and (iii) nontrivial quality guarantees? We answer this question in the affirmative, with FREDE(FREquent Directions Embedding), a sketching-based method that iteratively improves on quality while processing rows of the similarity matrix individually; thereby, it provides, at any iteration, column-covariance approximation guarantees that are, in due course, almost indistinguishable from those of the optimal row-covariance approximation by SVD. Our experimental evaluation on variably sized networks shows that FREDE performs as well as SVD and competitively against current state-of-the-art methods in diverse data mining tasks, even when it derives an embedding based on only 10% of node similarities.

Just SLaQ When You Approximate: Accurate Spectral Distances for Web-Scale Graphs

Graph comparison is a fundamental operation in data mining and information retrieval. Due to the combinatorial nature of graphs, it is hard to balance the expressiveness of the similarity measure and its scalability. Spectral analysis provides quintessential tools for studying the multi-scale structure of graphs and is a well-suited foundation for reasoning about differences between graphs. However, computing full spectrum of large graphs is computationally prohibitive; thus, spectral graph comparison methods often rely on rough approximation techniques with weak error guarantees. In this work, we propose SLaQ, an efficient and effective approximation technique for computing spectral distances between graphs with billions of nodes and edges. We derive the corresponding error bounds and demonstrate that accurate computation is possible in time linear in the number of graph edges. In a thorough experimental evaluation, we show that SLaQ outperforms existing methods, oftentimes by several orders of magnitude in approximation accuracy, and maintains comparable performance, allowing to compare million-scale graphs in a matter of minutes on a single machine.

Intrinsic Multi-scale Evaluation of Generative Models

Generative models are often used to sample high-dimensional data points from a manifold with small intrinsic dimension. Existing techniques for comparing generative models focus on global data properties such as mean and covariance; in that sense, they are extrinsic and uni-scale. We develop the first, to our knowledge, intrinsic and multi-scale method for characterizing and comparing underlying data manifolds, based on comparing all data moments by lower-bounding the spectral notion of the Gromov-Wasserstein distance between manifolds. In a thorough experimental study, we demonstrate that our method effectively evaluates the quality of generative models; further, we showcase its efficacy in discerning the disentanglement process in neural networks.

Quadrature-based features for kernel approximation

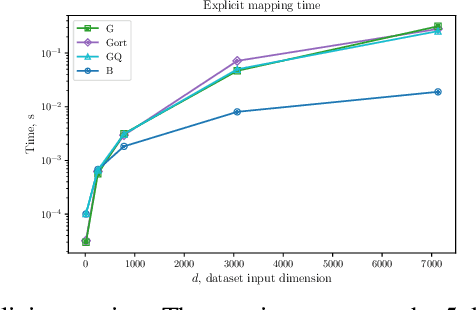
We consider the problem of improving kernel approximation via randomized feature maps. These maps arise as Monte Carlo approximation to integral representations of kernel functions and scale up kernel methods for larger datasets. Based on an efficient numerical integration technique, we propose a unifying approach that reinterprets the previous random features methods and extends to better estimates of the kernel approximation. We derive the convergence behaviour and conduct an extensive empirical study that supports our hypothesis.