One-Step Residual Shifting Diffusion for Image Super-Resolution via Distillation

Diffusion models for super-resolution (SR) produce high-quality visual results but require expensive computational costs. Despite the development of several methods to accelerate diffusion-based SR models, some (e.g., SinSR) fail to produce realistic perceptual details, while others (e.g., OSEDiff) may hallucinate non-existent structures. To overcome these issues, we present RSD, a new distillation method for ResShift, one of the top diffusion-based SR models. Our method is based on training the student network to produce such images that a new fake ResShift model trained on them will coincide with the teacher model. RSD achieves single-step restoration and outperforms the teacher by a large margin. We show that our distillation method can surpass the other distillation-based method for ResShift - SinSR - making it on par with state-of-the-art diffusion-based SR distillation methods. Compared to SR methods based on pre-trained text-to-image models, RSD produces competitive perceptual quality, provides images with better alignment to degraded input images, and requires fewer parameters and GPU memory. We provide experimental results on various real-world and synthetic datasets, including RealSR, RealSet65, DRealSR, ImageNet, and DIV2K.

InfoBridge: Mutual Information estimation via Bridge Matching

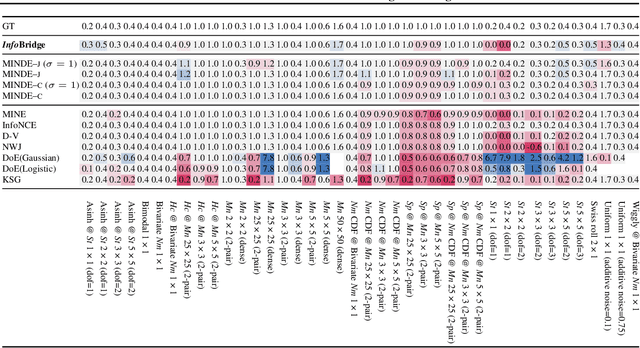
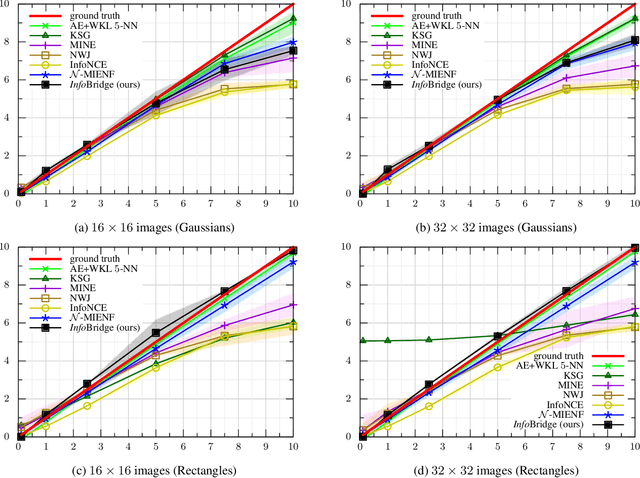
Diffusion bridge models have recently become a powerful tool in the field of generative modeling. In this work, we leverage their power to address another important problem in machine learning and information theory - the estimation of the mutual information (MI) between two random variables. We show that by using the theory of diffusion bridges, one can construct an unbiased estimator for data posing difficulties for conventional MI estimators. We showcase the performance of our estimator on a series of standard MI estimation benchmarks.

Inverse Bridge Matching Distillation

Learning diffusion bridge models is easy; making them fast and practical is an art. Diffusion bridge models (DBMs) are a promising extension of diffusion models for applications in image-to-image translation. However, like many modern diffusion and flow models, DBMs suffer from the problem of slow inference. To address it, we propose a novel distillation technique based on the inverse bridge matching formulation and derive the tractable objective to solve it in practice. Unlike previously developed DBM distillation techniques, the proposed method can distill both conditional and unconditional types of DBMs, distill models in a one-step generator, and use only the corrupted images for training. We evaluate our approach for both conditional and unconditional types of bridge matching on a wide set of setups, including super-resolution, JPEG restoration, sketch-to-image, and other tasks, and show that our distillation technique allows us to accelerate the inference of DBMs from 4x to 100x and even provide better generation quality than used teacher model depending on particular setup.

Diffusion & Adversarial Schrödinger Bridges via Iterative Proportional Markovian Fitting

The Iterative Markovian Fitting (IMF) procedure based on iterative reciprocal and Markovian projections has recently been proposed as a powerful method for solving the Schr\"odinger Bridge problem. However, it has been observed that for the practical implementation of this procedure, it is crucial to alternate between fitting a forward and backward time diffusion at each iteration. Such implementation is thought to be a practical heuristic, which is required to stabilize training and obtain good results in applications such as unpaired domain translation. In our work, we show that this heuristic closely connects with the pioneer approaches for the Schr\"odinger Bridge based on the Iterative Proportional Fitting (IPF) procedure. Namely, we find that the practical implementation of IMF is, in fact, a combination of IMF and IPF procedures, and we call this combination the Iterative Proportional Markovian Fitting (IPMF) procedure. We show both theoretically and practically that this combined IPMF procedure can converge under more general settings, thus, showing that the IPMF procedure opens a door towards developing a unified framework for solving Schr\"odinger Bridge problems.

Adversarial Schrödinger Bridge Matching

The Schr\"odinger Bridge (SB) problem offers a powerful framework for combining optimal transport and diffusion models. A promising recent approach to solve the SB problem is the Iterative Markovian Fitting (IMF) procedure, which alternates between Markovian and reciprocal projections of continuous-time stochastic processes. However, the model built by the IMF procedure has a long inference time due to using many steps of numerical solvers for stochastic differential equations. To address this limitation, we propose a novel Discrete-time IMF (D-IMF) procedure in which learning of stochastic processes is replaced by learning just a few transition probabilities in discrete time. Its great advantage is that in practice it can be naturally implemented using the Denoising Diffusion GAN (DD-GAN), an already well-established adversarial generative modeling technique. We show that our D-IMF procedure can provide the same quality of unpaired domain translation as the IMF, using only several generation steps instead of hundreds.

Light and Optimal Schrödinger Bridge Matching

Schr\"odinger Bridges (SB) have recently gained the attention of the ML community as a promising extension of classic diffusion models which is also interconnected to the Entropic Optimal Transport (EOT). Recent solvers for SB exploit the pervasive bridge matching procedures. Such procedures aim to recover a stochastic process transporting the mass between distributions given only a transport plan between them. In particular, given the EOT plan, these procedures can be adapted to solve SB. This fact is heavily exploited by recent works giving rives to matching-based SB solvers. The cornerstone here is recovering the EOT plan: recent works either use heuristical approximations (e.g., the minibatch OT) or establish iterative matching procedures which by the design accumulate the error during the training. We address these limitations and propose a novel procedure to learn SB which we call the \textbf{optimal Schr\"odinger bridge matching}. It exploits the optimal parameterization of the diffusion process and provably recovers the SB process \textbf{(a)} with a single bridge matching step and \textbf{(b)} with arbitrary transport plan as the input. Furthermore, we show that the optimal bridge matching objective coincides with the recently discovered energy-based modeling (EBM) objectives to learn EOT/SB. Inspired by this observation, we develop a light solver (which we call LightSB-M) to implement optimal matching in practice using the Gaussian mixture parameterization of the Schr\"odinger potential. We experimentally showcase the performance of our solver in a range of practical tasks. The code for the LightSB-M solver can be found at \url{https://github.com/SKholkin/LightSB-Matching}.

Light Schrödinger Bridge

Despite the recent advances in the field of computational Schrodinger Bridges (SB), most existing SB solvers are still heavy-weighted and require complex optimization of several neural networks. It turns out that there is no principal solver which plays the role of simple-yet-effective baseline for SB just like, e.g., $k$-means method in clustering, logistic regression in classification or Sinkhorn algorithm in discrete optimal transport. We address this issue and propose a novel fast and simple SB solver. Our development is a smart combination of two ideas which recently appeared in the field: (a) parameterization of the Schrodinger potentials with sum-exp quadratic functions and (b) viewing the log-Schrodinger potentials as the energy functions. We show that combined together these ideas yield a lightweight, simulation-free and theoretically justified SB solver with a simple straightforward optimization objective. As a result, it allows solving SB in moderate dimensions in a matter of minutes on CPU without a painful hyperparameter selection. Our light solver resembles the Gaussian mixture model which is widely used for density estimation. Inspired by this similarity, we also prove an important theoretical result showing that our light solver is a universal approximator of SBs. The code for the LightSB solver can be found at https://github.com/ngushchin/LightSB

Building the Bridge of Schrödinger: A Continuous Entropic Optimal Transport Benchmark

Over the last several years, there has been a significant progress in developing neural solvers for the Schr\"odinger Bridge (SB) problem and applying them to generative modeling. This new research field is justifiably fruitful as it is interconnected with the practically well-performing diffusion models and theoretically-grounded entropic optimal transport (EOT). Still the area lacks non-trivial tests allowing a researcher to understand how well do the methods solve SB or its equivalent continuous EOT problem. We fill this gap and propose a novel way to create pairs of probability distributions for which the ground truth OT solution in known by the construction. Our methodology is generic and works for a wide range of OT formulations, in particular, it covers the EOT which is equivalent to SB (the main interest of our study). This development allows us to create continuous benchmark distributions with the known EOT and SB solution on high-dimensional spaces such as spaces of images. As an illustration, we use these benchmark pairs to test how well do existing neural EOT/SB solvers actually compute the EOT solution. The benchmark is available via the link: https://github.com/ngushchin/EntropicOTBenchmark.

Entropic Neural Optimal Transport via Diffusion Processes

We propose a novel neural algorithm for the fundamental problem of computing the entropic optimal transport (EOT) plan between probability distributions which are accessible by samples. Our algorithm is based on the saddle point reformulation of the dynamic version of EOT which is known as the Schr\"odinger Bridge problem. In contrast to the prior methods for large-scale EOT, our algorithm is end-to-end and consists of a single learning step, has fast inference procedure, and allows handling small values of the entropy regularization coefficient which is of particular importance in some applied problems. Empirically, we show the performance of the method on several large-scale EOT tasks.