One-Step Residual Shifting Diffusion for Image Super-Resolution via Distillation

Diffusion models for super-resolution (SR) produce high-quality visual results but require expensive computational costs. Despite the development of several methods to accelerate diffusion-based SR models, some (e.g., SinSR) fail to produce realistic perceptual details, while others (e.g., OSEDiff) may hallucinate non-existent structures. To overcome these issues, we present RSD, a new distillation method for ResShift, one of the top diffusion-based SR models. Our method is based on training the student network to produce such images that a new fake ResShift model trained on them will coincide with the teacher model. RSD achieves single-step restoration and outperforms the teacher by a large margin. We show that our distillation method can surpass the other distillation-based method for ResShift - SinSR - making it on par with state-of-the-art diffusion-based SR distillation methods. Compared to SR methods based on pre-trained text-to-image models, RSD produces competitive perceptual quality, provides images with better alignment to degraded input images, and requires fewer parameters and GPU memory. We provide experimental results on various real-world and synthetic datasets, including RealSR, RealSet65, DRealSR, ImageNet, and DIV2K.

Inverse Bridge Matching Distillation

Learning diffusion bridge models is easy; making them fast and practical is an art. Diffusion bridge models (DBMs) are a promising extension of diffusion models for applications in image-to-image translation. However, like many modern diffusion and flow models, DBMs suffer from the problem of slow inference. To address it, we propose a novel distillation technique based on the inverse bridge matching formulation and derive the tractable objective to solve it in practice. Unlike previously developed DBM distillation techniques, the proposed method can distill both conditional and unconditional types of DBMs, distill models in a one-step generator, and use only the corrupted images for training. We evaluate our approach for both conditional and unconditional types of bridge matching on a wide set of setups, including super-resolution, JPEG restoration, sketch-to-image, and other tasks, and show that our distillation technique allows us to accelerate the inference of DBMs from 4x to 100x and even provide better generation quality than used teacher model depending on particular setup.

A3D: Does Diffusion Dream about 3D Alignment?

We tackle the problem of text-driven 3D generation from a geometry alignment perspective. We aim at the generation of multiple objects which are consistent in terms of semantics and geometry. Recent methods based on Score Distillation have succeeded in distilling the knowledge from 2D diffusion models to high-quality objects represented by 3D neural radiance fields. These methods handle multiple text queries separately, and therefore, the resulting objects have a high variability in object pose and structure. However, in some applications such as geometry editing, it is desirable to obtain aligned objects. In order to achieve alignment, we propose to optimize the continuous trajectories between the aligned objects, by modeling a space of linear pairwise interpolations of the textual embeddings with a single NeRF representation. We demonstrate that similar objects, consisting of semantically corresponding parts, can be well aligned in 3D space without costly modifications to the generation process. We provide several practical scenarios including mesh editing and object hybridization that benefit from geometry alignment and experimentally demonstrate the efficiency of our method. https://voyleg.github.io/a3d/

Adversarial Schrödinger Bridge Matching

The Schr\"odinger Bridge (SB) problem offers a powerful framework for combining optimal transport and diffusion models. A promising recent approach to solve the SB problem is the Iterative Markovian Fitting (IMF) procedure, which alternates between Markovian and reciprocal projections of continuous-time stochastic processes. However, the model built by the IMF procedure has a long inference time due to using many steps of numerical solvers for stochastic differential equations. To address this limitation, we propose a novel Discrete-time IMF (D-IMF) procedure in which learning of stochastic processes is replaced by learning just a few transition probabilities in discrete time. Its great advantage is that in practice it can be naturally implemented using the Denoising Diffusion GAN (DD-GAN), an already well-established adversarial generative modeling technique. We show that our D-IMF procedure can provide the same quality of unpaired domain translation as the IMF, using only several generation steps instead of hundreds.

NeuSD: Surface Completion with Multi-View Text-to-Image Diffusion

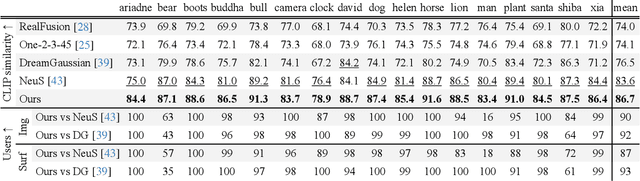
We present a novel method for 3D surface reconstruction from multiple images where only a part of the object of interest is captured. Our approach builds on two recent developments: surface reconstruction using neural radiance fields for the reconstruction of the visible parts of the surface, and guidance of pre-trained 2D diffusion models in the form of Score Distillation Sampling (SDS) to complete the shape in unobserved regions in a plausible manner. We introduce three components. First, we suggest employing normal maps as a pure geometric representation for SDS instead of color renderings which are entangled with the appearance information. Second, we introduce the freezing of the SDS noise during training which results in more coherent gradients and better convergence. Third, we propose Multi-View SDS as a way to condition the generation of the non-observable part of the surface without fine-tuning or making changes to the underlying 2D Stable Diffusion model. We evaluate our approach on the BlendedMVS dataset demonstrating significant qualitative and quantitative improvements over competing methods.

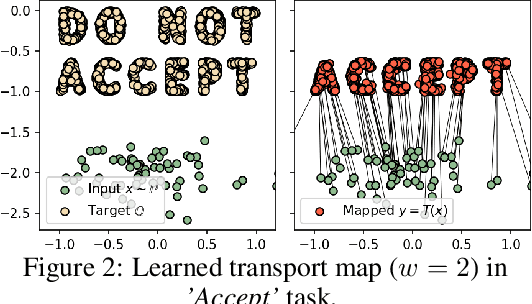
Extremal Domain Translation with Neural Optimal Transport

We propose the extremal transport (ET) which is a mathematical formalization of the theoretically best possible unpaired translation between a pair of domains w.r.t. the given similarity function. Inspired by the recent advances in neural optimal transport (OT), we propose a scalable algorithm to approximate ET maps as a limit of partial OT maps. We test our algorithm on toy examples and on the unpaired image-to-image translation task.

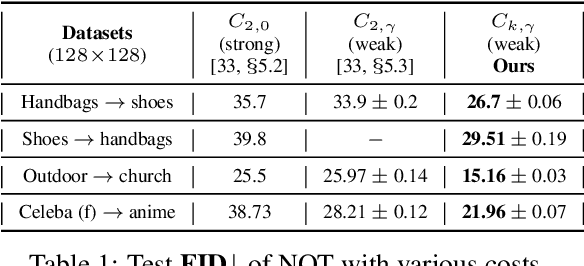
Kernel Neural Optimal Transport

We study the Neural Optimal Transport (NOT) algorithm which uses the general optimal transport formulation and learns stochastic transport plans. We show that NOT with the weak quadratic cost might learn fake plans which are not optimal. To resolve this issue, we introduce kernel weak quadratic costs. We show that they provide improved theoretical guarantees and practical performance. We test NOT with kernel costs on the unpaired image-to-image translation task.

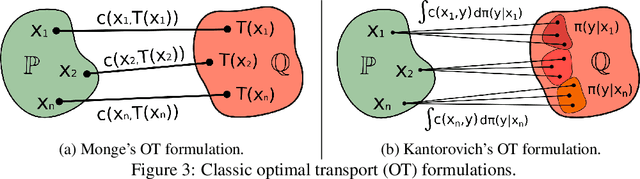
Neural Optimal Transport

We present a novel neural-networks-based algorithm to compute optimal transport maps and plans for strong and weak transport costs. To justify the usage of neural networks, we prove that they are universal approximators of transport plans between probability distributions. We evaluate the performance of our optimal transport algorithm on toy examples and on the unpaired image-to-image style translation task.

DeepRLS: A Recurrent Network Architecture with Least Squares Implicit Layers for Non-blind Image Deconvolution

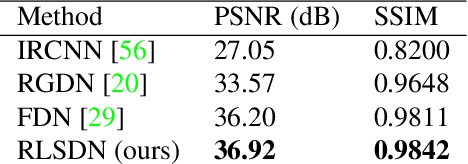
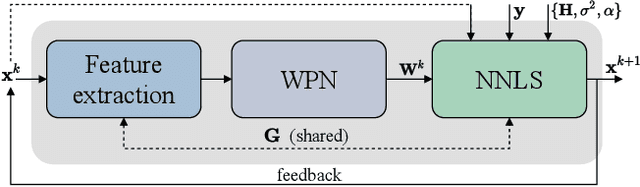
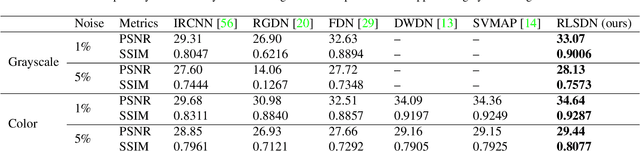
In this work, we study the problem of non-blind image deconvolution and propose a novel recurrent network architecture that leads to very competitive restoration results of high image quality. Motivated by the computational efficiency and robustness of existing large scale linear solvers, we manage to express the solution to this problem as the solution of a series of adaptive non-negative least-squares problems. This gives rise to our proposed Recurrent Least Squares Deconvolution Network (RLSDN) architecture, which consists of an implicit layer that imposes a linear constraint between its input and output. By design, our network manages to serve two important purposes simultaneously. The first is that it implicitly models an effective image prior that can adequately characterize the set of natural images, while the second is that it recovers the corresponding maximum a posteriori (MAP) estimate. Experiments on publicly available datasets, comparing recent state-of-the-art methods, show that our proposed RLSDN approach achieves the best reported performance both for grayscale and color images for all tested scenarios. Furthermore, we introduce a novel training strategy that can be adopted by any network architecture that involves the solution of linear systems as part of its pipeline. Our strategy eliminates completely the need to unroll the iterations required by the linear solver and, thus, it reduces significantly the memory footprint during training. Consequently, this enables the training of deeper network architectures which can further improve the reconstruction results.

Ex$^2$MCMC: Sampling through Exploration Exploitation

We develop an Explore-Exploit Markov chain Monte Carlo algorithm ($\operatorname{Ex^2MCMC}$) that combines multiple global proposals and local moves. The proposed method is massively parallelizable and extremely computationally efficient. We prove $V$-uniform geometric ergodicity of $\operatorname{Ex^2MCMC}$ under realistic conditions and compute explicit bounds on the mixing rate showing the improvement brought by the multiple global moves. We show that $\operatorname{Ex^2MCMC}$ allows fine-tuning of exploitation (local moves) and exploration (global moves) via a novel approach to proposing dependent global moves. Finally, we develop an adaptive scheme, $\operatorname{FlEx^2MCMC}$, that learns the distribution of global moves using normalizing flows. We illustrate the efficiency of $\operatorname{Ex^2MCMC}$ and its adaptive versions on many classical sampling benchmarks. We also show that these algorithms improve the quality of sampling GANs as energy-based models.