A Statistical Learning Perspective on Semi-dual Adversarial Neural Optimal Transport Solvers

Neural network based Optimal Transport (OT) is a recent and fruitful direction in the generative modeling community. It finds its applications in various fields such as domain translation, image super-resolution, computational biology and others. Among the existing approaches to OT, of considerable interest are adversarial minimax solvers based on semi-dual formulations of OT problems. While promising, these methods lack theoretical investigation from a statistical learning perspective. Our work fills this gap by establishing upper bounds on the generalization error of an approximate OT map recovered by the minimax quadratic OT solver. Importantly, the bounds we derive depend solely on some standard statistical and mathematical properties of the considered functional classes (neural networks). While our analysis focuses on the quadratic OT, we believe that similar bounds could be derived for more general OT formulations, paving the promising direction for future research.

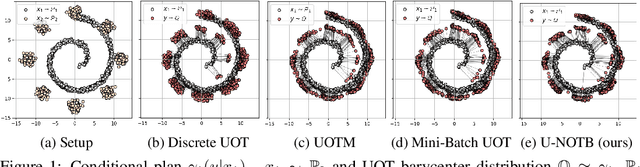
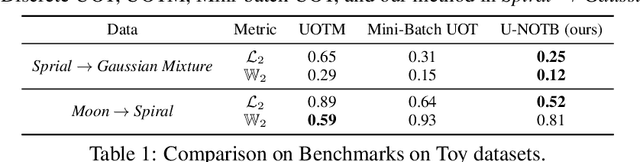
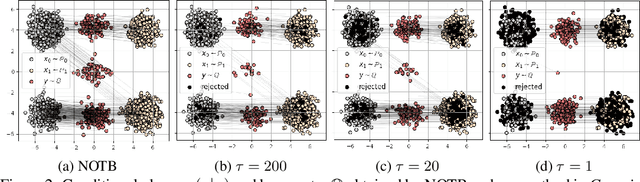
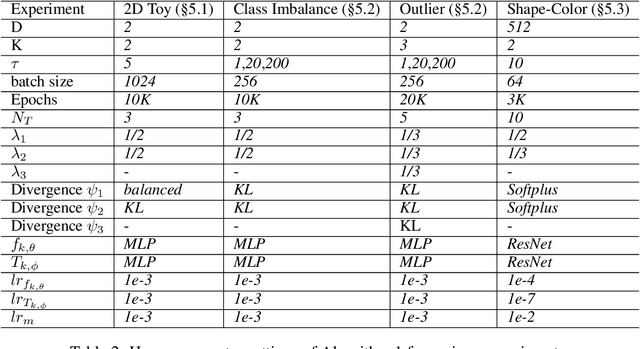
Robust Barycenter Estimation using Semi-Unbalanced Neural Optimal Transport

A common challenge in aggregating data from multiple sources can be formalized as an \textit{Optimal Transport} (OT) barycenter problem, which seeks to compute the average of probability distributions with respect to OT discrepancies. However, the presence of outliers and noise in the data measures can significantly hinder the performance of traditional statistical methods for estimating OT barycenters. To address this issue, we propose a novel, scalable approach for estimating the \textit{robust} continuous barycenter, leveraging the dual formulation of the \textit{(semi-)unbalanced} OT problem. To the best of our knowledge, this paper is the first attempt to develop an algorithm for robust barycenters under the continuous distribution setup. Our method is framed as a $\min$-$\max$ optimization problem and is adaptable to \textit{general} cost function. We rigorously establish the theoretical underpinnings of the proposed method and demonstrate its robustness to outliers and class imbalance through a number of illustrative experiments.

Estimating Barycenters of Distributions with Neural Optimal Transport

Given a collection of probability measures, a practitioner sometimes needs to find an "average" distribution which adequately aggregates reference distributions. A theoretically appealing notion of such an average is the Wasserstein barycenter, which is the primal focus of our work. By building upon the dual formulation of Optimal Transport (OT), we propose a new scalable approach for solving the Wasserstein barycenter problem. Our methodology is based on the recent Neural OT solver: it has bi-level adversarial learning objective and works for general cost functions. These are key advantages of our method, since the typical adversarial algorithms leveraging barycenter tasks utilize tri-level optimization and focus mostly on quadratic cost. We also establish theoretical error bounds for our proposed approach and showcase its applicability and effectiveness on illustrative scenarios and image data setups.

Energy-Guided Continuous Entropic Barycenter Estimation for General Costs

Optimal transport (OT) barycenters are a mathematically grounded way of averaging probability distributions while capturing their geometric properties. In short, the barycenter task is to take the average of a collection of probability distributions w.r.t. given OT discrepancies. We propose a novel algorithm for approximating the continuous Entropic OT (EOT) barycenter for arbitrary OT cost functions. Our approach is built upon the dual reformulation of the EOT problem based on weak OT, which has recently gained the attention of the ML community. Beyond its novelty, our method enjoys several advantageous properties: (i) we establish quality bounds for the recovered solution; (ii) this approach seemlessly interconnects with the Energy-Based Models (EBMs) learning procedure enabling the use of well-tuned algorithms for the problem of interest; (iii) it provides an intuitive optimization scheme avoiding min-max, reinforce and other intricate technical tricks. For validation, we consider several low-dimensional scenarios and image-space setups, including non-Euclidean cost functions. Furthermore, we investigate the practical task of learning the barycenter on an image manifold generated by a pretrained generative model, opening up new directions for real-world applications.

Partial Neural Optimal Transport

We propose a novel neural method to compute partial optimal transport (OT) maps, i.e., OT maps between parts of measures of the specified masses. We test our partial neural optimal transport algorithm on synthetic examples.

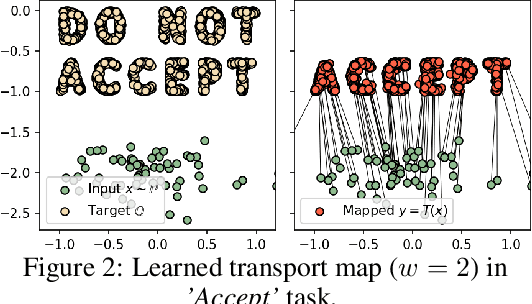
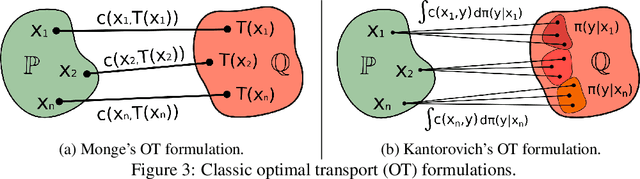
Extremal Domain Translation with Neural Optimal Transport

We propose the extremal transport (ET) which is a mathematical formalization of the theoretically best possible unpaired translation between a pair of domains w.r.t. the given similarity function. Inspired by the recent advances in neural optimal transport (OT), we propose a scalable algorithm to approximate ET maps as a limit of partial OT maps. We test our algorithm on toy examples and on the unpaired image-to-image translation task.

Unpaired Image Super-Resolution with Optimal Transport Maps

Real-world image super-resolution (SR) tasks often do not have paired datasets limiting the application of supervised techniques. As a result, the tasks are usually approached by unpaired techniques based on Generative Adversarial Networks (GANs) which yield complex training losses with several regularization terms such as content and identity losses. We theoretically investigate the optimization problems which arise in such models and find two surprising observations. First, the learned SR map is always an optimal transport (OT) map. Second, we empirically show that the learned map is biased, i.e., it may not actually transform the distribution of low-resolution images to high-resolution images. Inspired by these findings, we propose an algorithm for unpaired SR which learns an unbiased OT map for the perceptual transport cost. Unlike existing GAN-based alternatives, our algorithm has a simple optimization objective reducing the neccesity to perform complex hyperparameter selection and use additional regularizations. At the same time, it provides nearly state-of-the-art performance on the large-scale unpaired AIM-19 dataset.

Can We Use Neural Regularization to Solve Depth Super-Resolution?

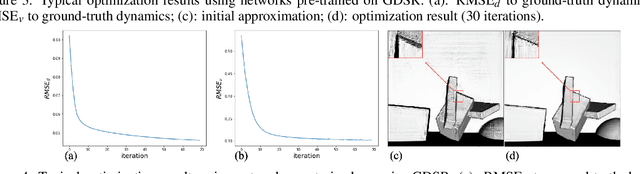
Depth maps captured with commodity sensors often require super-resolution to be used in applications. In this work we study a super-resolution approach based on a variational problem statement with Tikhonov regularization where the regularizer is parametrized with a deep neural network. This approach was previously applied successfully in photoacoustic tomography. We experimentally show that its application to depth map super-resolution is difficult, and provide suggestions about the reasons for that.