Litu Rout
EntRGi: Entropy Aware Reward Guidance for Diffusion Language Models
Feb 04, 2026Abstract:Reward guidance has been applied to great success in the test-time adaptation of continuous diffusion models; it updates each denoising step using the gradients from a downstream reward model. We study reward guidance for discrete diffusion language models, where one cannot differentiate through the natural outputs of the model because they are discrete tokens. Existing approaches either replace these discrete tokens with continuous relaxations, or employ techniques like the straight-through estimator. In this work, we show the downsides of both these methods. The former degrades gradient feedback because the reward model has never been trained with continuous inputs. The latter involves incorrect optimization because the gradient evaluated at discrete tokens is used to update continuous logits. Our key innovation is to go beyond this tradeoff by introducing a novel mechanism called EntRGi: Entropy aware Reward Guidance that dynamically regulates the gradients from the reward model. By modulating the continuous relaxation using the model's confidence, our approach substantially improves reward guidance while providing reliable inputs to the reward model. We empirically validate our approach on a 7B-parameter diffusion language model across 3 diverse reward models and 3 multi-skill benchmarks, showing consistent improvements over state-of-the-art methods.
Test-Time Anchoring for Discrete Diffusion Posterior Sampling
Oct 02, 2025Abstract:We study the problem of posterior sampling using pretrained discrete diffusion foundation models, aiming to recover images from noisy measurements without retraining task-specific models. While diffusion models have achieved remarkable success in generative modeling, most advances rely on continuous Gaussian diffusion. In contrast, discrete diffusion offers a unified framework for jointly modeling categorical data such as text and images. Beyond unification, discrete diffusion provides faster inference, finer control, and principled training-free Bayesian inference, making it particularly well-suited for posterior sampling. However, existing approaches to discrete diffusion posterior sampling face severe challenges: derivative-free guidance yields sparse signals, continuous relaxations limit applicability, and split Gibbs samplers suffer from the curse of dimensionality. To overcome these limitations, we introduce Anchored Posterior Sampling (APS) for masked diffusion foundation models, built on two key innovations -- quantized expectation for gradient-like guidance in discrete embedding space, and anchored remasking for adaptive decoding. Our approach achieves state-of-the-art performance among discrete diffusion samplers across linear and nonlinear inverse problems on the standard benchmarks. We further demonstrate the benefits of our approach in training-free stylization and text-guided editing.
Efficient Approximate Posterior Sampling with Annealed Langevin Monte Carlo
Aug 11, 2025Abstract:We study the problem of posterior sampling in the context of score based generative models. We have a trained score network for a prior $p(x)$, a measurement model $p(y|x)$, and are tasked with sampling from the posterior $p(x|y)$. Prior work has shown this to be intractable in KL (in the worst case) under well-accepted computational hardness assumptions. Despite this, popular algorithms for tasks such as image super-resolution, stylization, and reconstruction enjoy empirical success. Rather than establishing distributional assumptions or restricted settings under which exact posterior sampling is tractable, we view this as a more general "tilting" problem of biasing a distribution towards a measurement. Under minimal assumptions, we show that one can tractably sample from a distribution that is simultaneously close to the posterior of a noised prior in KL divergence and the true posterior in Fisher divergence. Intuitively, this combination ensures that the resulting sample is consistent with both the measurement and the prior. To the best of our knowledge these are the first formal results for (approximate) posterior sampling in polynomial time.
Anchored Diffusion Language Model
May 24, 2025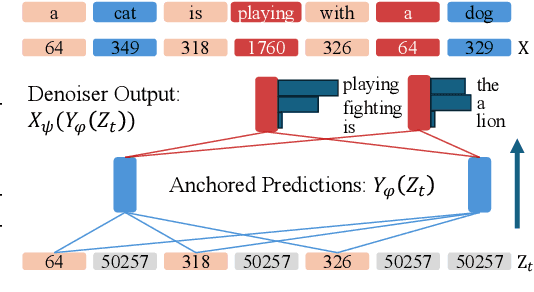
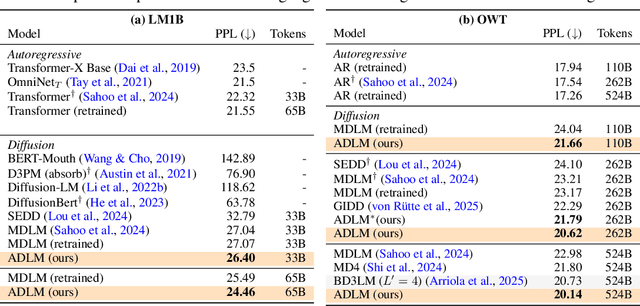
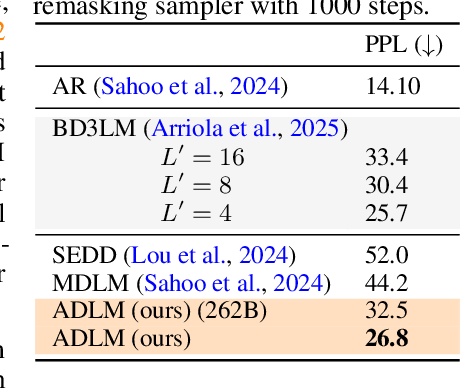
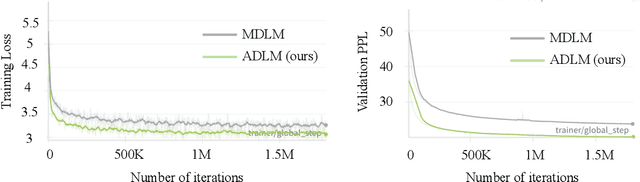
Abstract:Diffusion Language Models (DLMs) promise parallel generation and bidirectional context, yet they underperform autoregressive (AR) models in both likelihood modeling and generated text quality. We identify that this performance gap arises when important tokens (e.g., key words or low-frequency words that anchor a sentence) are masked early in the forward process, limiting contextual information for accurate reconstruction. To address this, we introduce the Anchored Diffusion Language Model (ADLM), a novel two-stage framework that first predicts distributions over important tokens via an anchor network, and then predicts the likelihoods of missing tokens conditioned on the anchored predictions. ADLM significantly improves test perplexity on LM1B and OpenWebText, achieving up to 25.4% gains over prior DLMs, and narrows the gap with strong AR baselines. It also achieves state-of-the-art performance in zero-shot generalization across seven benchmarks and surpasses AR models in MAUVE score, which marks the first time a DLM generates better human-like text than an AR model. Theoretically, we derive an Anchored Negative Evidence Lower Bound (ANELBO) objective and show that anchoring improves sample complexity and likelihood modeling. Beyond diffusion, anchoring boosts performance in AR models and enhances reasoning in math and logic tasks, outperforming existing chain-of-thought approaches
Constrained Posterior Sampling: Time Series Generation with Hard Constraints
Oct 16, 2024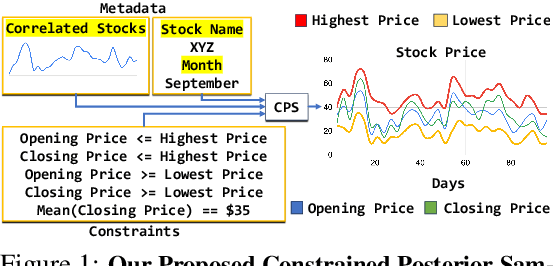
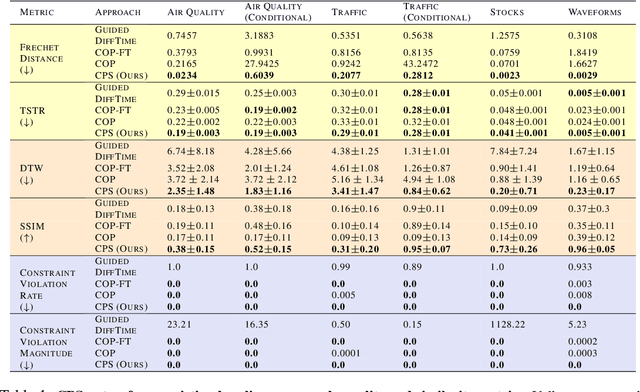
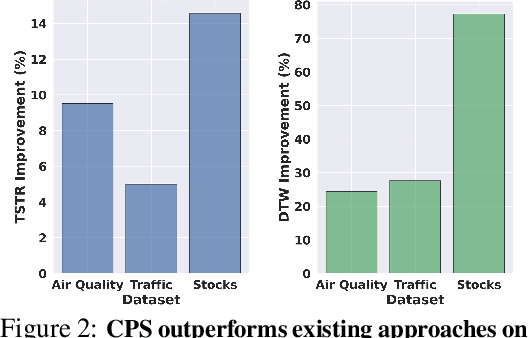

Abstract:Generating realistic time series samples is crucial for stress-testing models and protecting user privacy by using synthetic data. In engineering and safety-critical applications, these samples must meet certain hard constraints that are domain-specific or naturally imposed by physics or nature. Consider, for example, generating electricity demand patterns with constraints on peak demand times. This can be used to stress-test the functioning of power grids during adverse weather conditions. Existing approaches for generating constrained time series are either not scalable or degrade sample quality. To address these challenges, we introduce Constrained Posterior Sampling (CPS), a diffusion-based sampling algorithm that aims to project the posterior mean estimate into the constraint set after each denoising update. Notably, CPS scales to a large number of constraints (~100) without requiring additional training. We provide theoretical justifications highlighting the impact of our projection step on sampling. Empirically, CPS outperforms state-of-the-art methods in sample quality and similarity to real time series by around 10% and 42%, respectively, on real-world stocks, traffic, and air quality datasets.
Semantic Image Inversion and Editing using Rectified Stochastic Differential Equations
Oct 14, 2024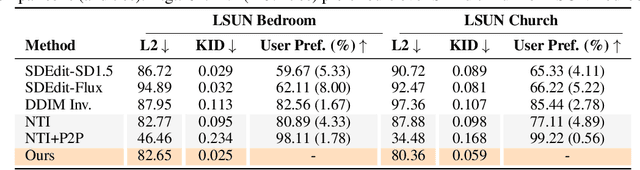
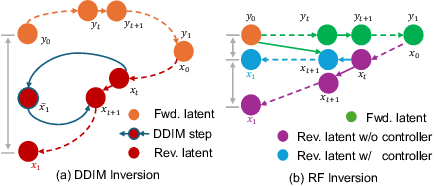

Abstract:Generative models transform random noise into images; their inversion aims to transform images back to structured noise for recovery and editing. This paper addresses two key tasks: (i) inversion and (ii) editing of a real image using stochastic equivalents of rectified flow models (such as Flux). Although Diffusion Models (DMs) have recently dominated the field of generative modeling for images, their inversion presents faithfulness and editability challenges due to nonlinearities in drift and diffusion. Existing state-of-the-art DM inversion approaches rely on training of additional parameters or test-time optimization of latent variables; both are expensive in practice. Rectified Flows (RFs) offer a promising alternative to diffusion models, yet their inversion has been underexplored. We propose RF inversion using dynamic optimal control derived via a linear quadratic regulator. We prove that the resulting vector field is equivalent to a rectified stochastic differential equation. Additionally, we extend our framework to design a stochastic sampler for Flux. Our inversion method allows for state-of-the-art performance in zero-shot inversion and editing, outperforming prior works in stroke-to-image synthesis and semantic image editing, with large-scale human evaluations confirming user preference.
RB-Modulation: Training-Free Personalization of Diffusion Models using Stochastic Optimal Control
May 27, 2024
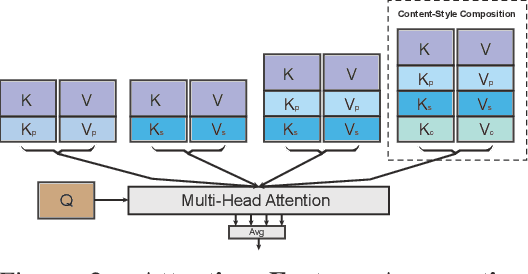
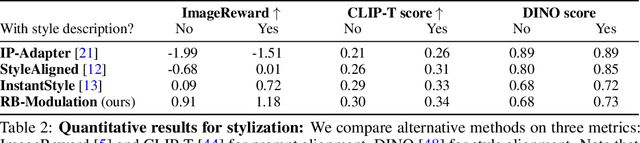
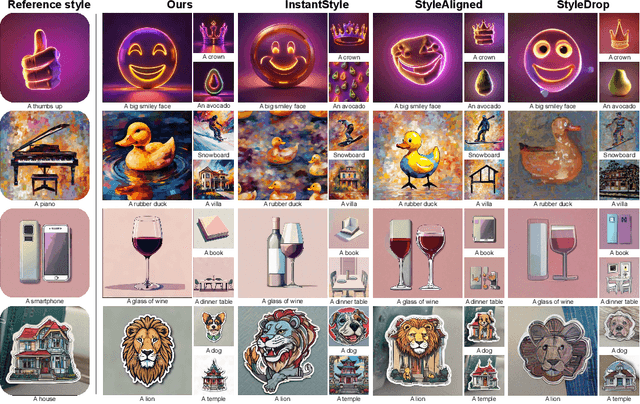
Abstract:We propose Reference-Based Modulation (RB-Modulation), a new plug-and-play solution for training-free personalization of diffusion models. Existing training-free approaches exhibit difficulties in (a) style extraction from reference images in the absence of additional style or content text descriptions, (b) unwanted content leakage from reference style images, and (c) effective composition of style and content. RB-Modulation is built on a novel stochastic optimal controller where a style descriptor encodes the desired attributes through a terminal cost. The resulting drift not only overcomes the difficulties above, but also ensures high fidelity to the reference style and adheres to the given text prompt. We also introduce a cross-attention-based feature aggregation scheme that allows RB-Modulation to decouple content and style from the reference image. With theoretical justification and empirical evidence, our framework demonstrates precise extraction and control of content and style in a training-free manner. Further, our method allows a seamless composition of content and style, which marks a departure from the dependency on external adapters or ControlNets.
Beyond First-Order Tweedie: Solving Inverse Problems using Latent Diffusion
Dec 01, 2023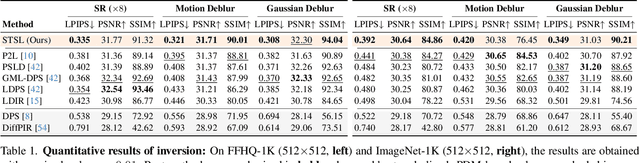

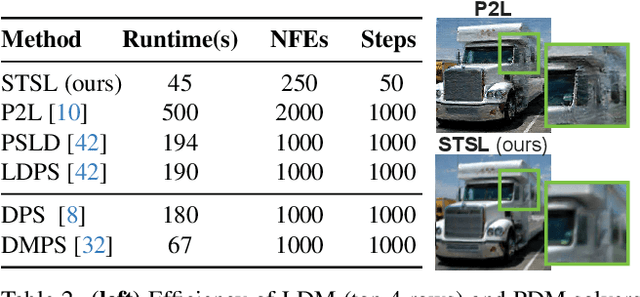

Abstract:Sampling from the posterior distribution poses a major computational challenge in solving inverse problems using latent diffusion models. Common methods rely on Tweedie's first-order moments, which are known to induce a quality-limiting bias. Existing second-order approximations are impractical due to prohibitive computational costs, making standard reverse diffusion processes intractable for posterior sampling. This paper introduces Second-order Tweedie sampler from Surrogate Loss (STSL), a novel sampler that offers efficiency comparable to first-order Tweedie with a tractable reverse process using second-order approximation. Our theoretical results reveal that the second-order approximation is lower bounded by our surrogate loss that only requires $O(1)$ compute using the trace of the Hessian, and by the lower bound we derive a new drift term to make the reverse process tractable. Our method surpasses SoTA solvers PSLD and P2L, achieving 4X and 8X reduction in neural function evaluations, respectively, while notably enhancing sampling quality on FFHQ, ImageNet, and COCO benchmarks. In addition, we show STSL extends to text-guided image editing and addresses residual distortions present from corrupted images in leading text-guided image editing methods. To our best knowledge, this is the first work to offer an efficient second-order approximation in solving inverse problems using latent diffusion and editing real-world images with corruptions.
Solving Linear Inverse Problems Provably via Posterior Sampling with Latent Diffusion Models
Jul 02, 2023



Abstract:We present the first framework to solve linear inverse problems leveraging pre-trained latent diffusion models. Previously proposed algorithms (such as DPS and DDRM) only apply to pixel-space diffusion models. We theoretically analyze our algorithm showing provable sample recovery in a linear model setting. The algorithmic insight obtained from our analysis extends to more general settings often considered in practice. Experimentally, we outperform previously proposed posterior sampling algorithms in a wide variety of problems including random inpainting, block inpainting, denoising, deblurring, destriping, and super-resolution.
Beyond Uniform Smoothness: A Stopped Analysis of Adaptive SGD
Feb 13, 2023Abstract:This work considers the problem of finding a first-order stationary point of a non-convex function with potentially unbounded smoothness constant using a stochastic gradient oracle. We focus on the class of $(L_0,L_1)$-smooth functions proposed by Zhang et al. (ICLR'20). Empirical evidence suggests that these functions more closely captures practical machine learning problems as compared to the pervasive $L_0$-smoothness. This class is rich enough to include highly non-smooth functions, such as $\exp(L_1 x)$ which is $(0,\mathcal{O}(L_1))$-smooth. Despite the richness, an emerging line of works achieves the $\widetilde{\mathcal{O}}(\frac{1}{\sqrt{T}})$ rate of convergence when the noise of the stochastic gradients is deterministically and uniformly bounded. This noise restriction is not required in the $L_0$-smooth setting, and in many practical settings is either not satisfied, or results in weaker convergence rates with respect to the noise scaling of the convergence rate. We develop a technique that allows us to prove $\mathcal{O}(\frac{\mathrm{poly}\log(T)}{\sqrt{T}})$ convergence rates for $(L_0,L_1)$-smooth functions without assuming uniform bounds on the noise support. The key innovation behind our results is a carefully constructed stopping time $\tau$ which is simultaneously "large" on average, yet also allows us to treat the adaptive step sizes before $\tau$ as (roughly) independent of the gradients. For general $(L_0,L_1)$-smooth functions, our analysis requires the mild restriction that the multiplicative noise parameter $\sigma_1 < 1$. For a broad subclass of $(L_0,L_1)$-smooth functions, our convergence rate continues to hold when $\sigma_1 \geq 1$. By contrast, we prove that many algorithms analyzed by prior works on $(L_0,L_1)$-smooth optimization diverge with constant probability even for smooth and strongly-convex functions when $\sigma_1 > 1$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge