In-Context Fine-Tuning for Time-Series Foundation Models

Motivated by the recent success of time-series foundation models for zero-shot forecasting, we present a methodology for $\textit{in-context fine-tuning}$ of a time-series foundation model. In particular, we design a pretrained foundation model that can be prompted (at inference time) with multiple time-series examples, in order to forecast a target time-series into the future. Our foundation model is specifically trained to utilize examples from multiple related time-series in its context window (in addition to the history of the target time-series) to help it adapt to the specific distribution of the target domain at inference time. We show that such a foundation model that uses in-context examples at inference time can obtain much better performance on popular forecasting benchmarks compared to supervised deep learning methods, statistical models, as well as other time-series foundation models. Interestingly, our in-context fine-tuning approach even rivals the performance of a foundation model that is explicitly fine-tuned on the target domain.

Beyond Uniform Smoothness: A Stopped Analysis of Adaptive SGD

This work considers the problem of finding a first-order stationary point of a non-convex function with potentially unbounded smoothness constant using a stochastic gradient oracle. We focus on the class of $(L_0,L_1)$-smooth functions proposed by Zhang et al. (ICLR'20). Empirical evidence suggests that these functions more closely captures practical machine learning problems as compared to the pervasive $L_0$-smoothness. This class is rich enough to include highly non-smooth functions, such as $\exp(L_1 x)$ which is $(0,\mathcal{O}(L_1))$-smooth. Despite the richness, an emerging line of works achieves the $\widetilde{\mathcal{O}}(\frac{1}{\sqrt{T}})$ rate of convergence when the noise of the stochastic gradients is deterministically and uniformly bounded. This noise restriction is not required in the $L_0$-smooth setting, and in many practical settings is either not satisfied, or results in weaker convergence rates with respect to the noise scaling of the convergence rate. We develop a technique that allows us to prove $\mathcal{O}(\frac{\mathrm{poly}\log(T)}{\sqrt{T}})$ convergence rates for $(L_0,L_1)$-smooth functions without assuming uniform bounds on the noise support. The key innovation behind our results is a carefully constructed stopping time $\tau$ which is simultaneously "large" on average, yet also allows us to treat the adaptive step sizes before $\tau$ as (roughly) independent of the gradients. For general $(L_0,L_1)$-smooth functions, our analysis requires the mild restriction that the multiplicative noise parameter $\sigma_1 < 1$. For a broad subclass of $(L_0,L_1)$-smooth functions, our convergence rate continues to hold when $\sigma_1 \geq 1$. By contrast, we prove that many algorithms analyzed by prior works on $(L_0,L_1)$-smooth optimization diverge with constant probability even for smooth and strongly-convex functions when $\sigma_1 > 1$.

The Power of Adaptivity in SGD: Self-Tuning Step Sizes with Unbounded Gradients and Affine Variance

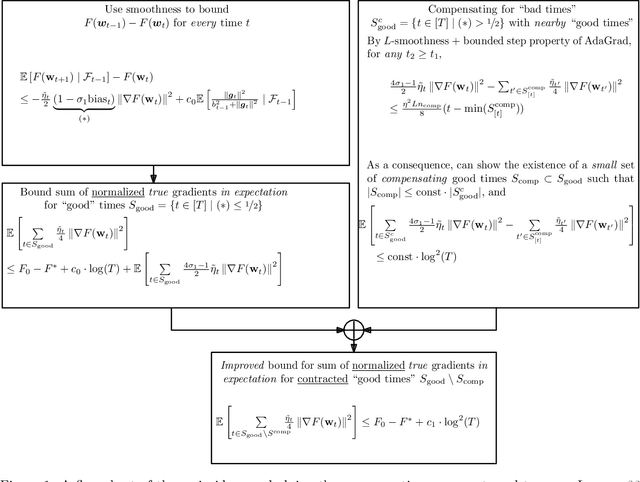
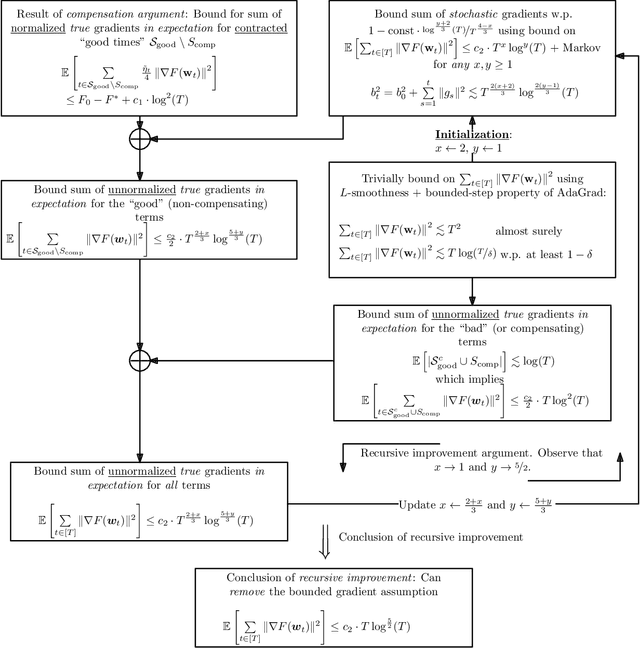
We study convergence rates of AdaGrad-Norm as an exemplar of adaptive stochastic gradient methods (SGD), where the step sizes change based on observed stochastic gradients, for minimizing non-convex, smooth objectives. Despite their popularity, the analysis of adaptive SGD lags behind that of non adaptive methods in this setting. Specifically, all prior works rely on some subset of the following assumptions: (i) uniformly-bounded gradient norms, (ii) uniformly-bounded stochastic gradient variance (or even noise support), (iii) conditional independence between the step size and stochastic gradient. In this work, we show that AdaGrad-Norm exhibits an order optimal convergence rate of $\mathcal{O}\left(\frac{\mathrm{poly}\log(T)}{\sqrt{T}}\right)$ after $T$ iterations under the same assumptions as optimally-tuned non adaptive SGD (unbounded gradient norms and affine noise variance scaling), and crucially, without needing any tuning parameters. We thus establish that adaptive gradient methods exhibit order-optimal convergence in much broader regimes than previously understood.

Mix and Match: An Optimistic Tree-Search Approach for Learning Models from Mixture Distributions

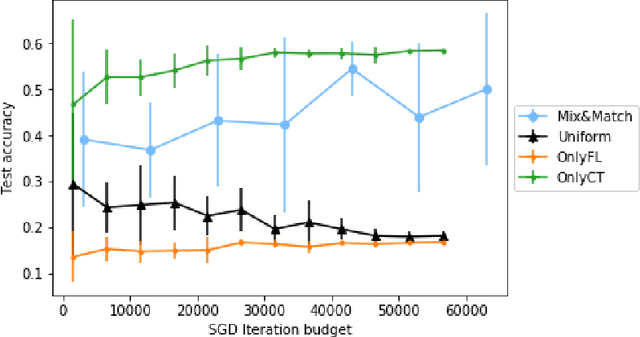
We consider a co-variate shift problem where one has access to several marginally different training datasets for the same learning problem and a small validation set which possibly differs from all the individual training distributions. This co-variate shift is caused, in part, due to unobserved features in the datasets. The objective, then, is to find the best mixture distribution over the training datasets (with only observed features) such that training a learning algorithm using this mixture has the best validation performance. Our proposed algorithm, ${\sf Mix\&Match}$, combines stochastic gradient descent (SGD) with optimistic tree search and model re-use (evolving partially trained models with samples from different mixture distributions) over the space of mixtures, for this task. We prove simple regret guarantees for our algorithm with respect to recovering the optimal mixture, given a total budget of SGD evaluations. Finally, we validate our algorithm on two real-world datasets.