Straggler-Resilient Personalized Federated Learning

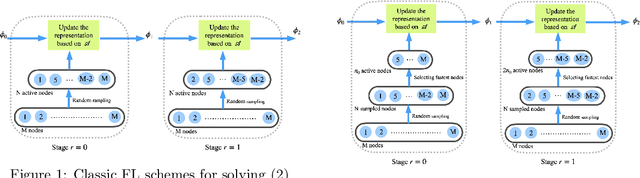
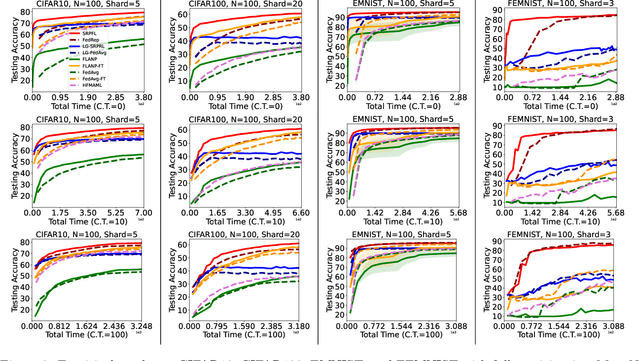
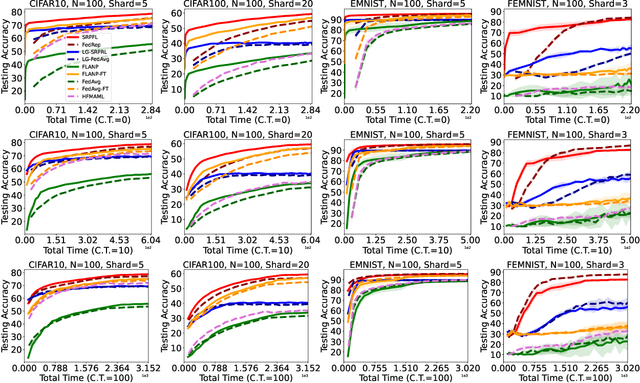
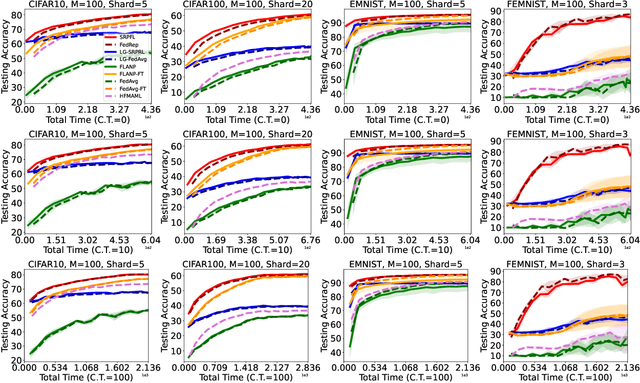
Federated Learning is an emerging learning paradigm that allows training models from samples distributed across a large network of clients while respecting privacy and communication restrictions. Despite its success, federated learning faces several challenges related to its decentralized nature. In this work, we develop a novel algorithmic procedure with theoretical speedup guarantees that simultaneously handles two of these hurdles, namely (i) data heterogeneity, i.e., data distributions can vary substantially across clients, and (ii) system heterogeneity, i.e., the computational power of the clients could differ significantly. Our method relies on ideas from representation learning theory to find a global common representation using all clients' data and learn a user-specific set of parameters leading to a personalized solution for each client. Furthermore, our method mitigates the effects of stragglers by adaptively selecting clients based on their computational characteristics and statistical significance, thus achieving, for the first time, near optimal sample complexity and provable logarithmic speedup. Experimental results support our theoretical findings showing the superiority of our method over alternative personalized federated schemes in system and data heterogeneous environments.

The Power of Adaptivity in SGD: Self-Tuning Step Sizes with Unbounded Gradients and Affine Variance

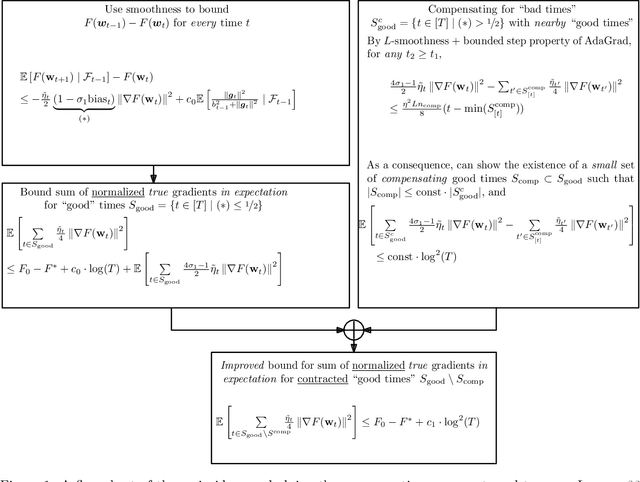
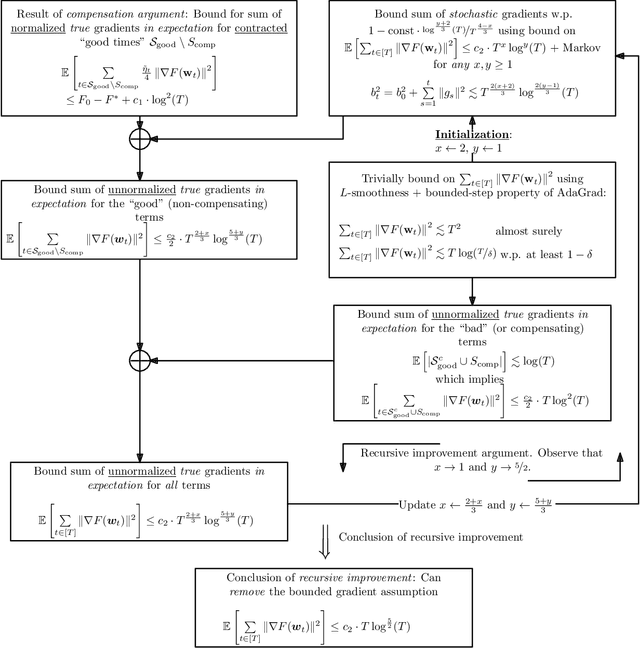
We study convergence rates of AdaGrad-Norm as an exemplar of adaptive stochastic gradient methods (SGD), where the step sizes change based on observed stochastic gradients, for minimizing non-convex, smooth objectives. Despite their popularity, the analysis of adaptive SGD lags behind that of non adaptive methods in this setting. Specifically, all prior works rely on some subset of the following assumptions: (i) uniformly-bounded gradient norms, (ii) uniformly-bounded stochastic gradient variance (or even noise support), (iii) conditional independence between the step size and stochastic gradient. In this work, we show that AdaGrad-Norm exhibits an order optimal convergence rate of $\mathcal{O}\left(\frac{\mathrm{poly}\log(T)}{\sqrt{T}}\right)$ after $T$ iterations under the same assumptions as optimally-tuned non adaptive SGD (unbounded gradient norms and affine noise variance scaling), and crucially, without needing any tuning parameters. We thus establish that adaptive gradient methods exhibit order-optimal convergence in much broader regimes than previously understood.

Straggler-Resilient Federated Learning: Leveraging the Interplay Between Statistical Accuracy and System Heterogeneity

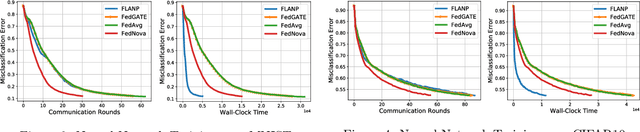
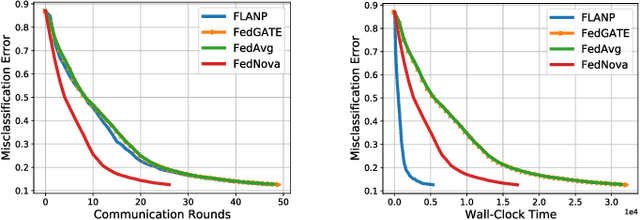
Federated Learning is a novel paradigm that involves learning from data samples distributed across a large network of clients while the data remains local. It is, however, known that federated learning is prone to multiple system challenges including system heterogeneity where clients have different computation and communication capabilities. Such heterogeneity in clients' computation speeds has a negative effect on the scalability of federated learning algorithms and causes significant slow-down in their runtime due to the existence of stragglers. In this paper, we propose a novel straggler-resilient federated learning method that incorporates statistical characteristics of the clients' data to adaptively select the clients in order to speed up the learning procedure. The key idea of our algorithm is to start the training procedure with faster nodes and gradually involve the slower nodes in the model training once the statistical accuracy of the data corresponding to the current participating nodes is reached. The proposed approach reduces the overall runtime required to achieve the statistical accuracy of data of all nodes, as the solution for each stage is close to the solution of the subsequent stage with more samples and can be used as a warm-start. Our theoretical results characterize the speedup gain in comparison to standard federated benchmarks for strongly convex objectives, and our numerical experiments also demonstrate significant speedups in wall-clock time of our straggler-resilient method compared to federated learning benchmarks.