Straggler-Resilient Personalized Federated Learning
Paper and Code
Jun 05, 2022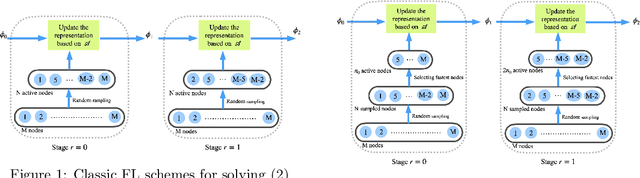
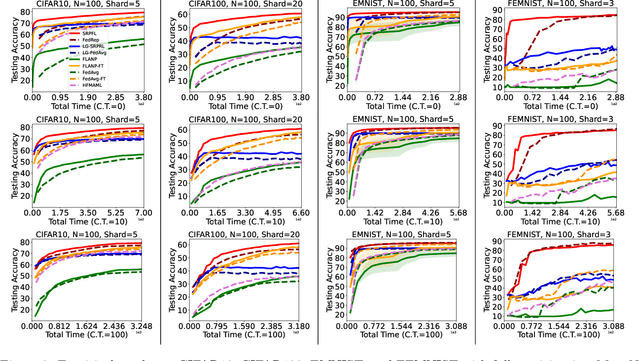
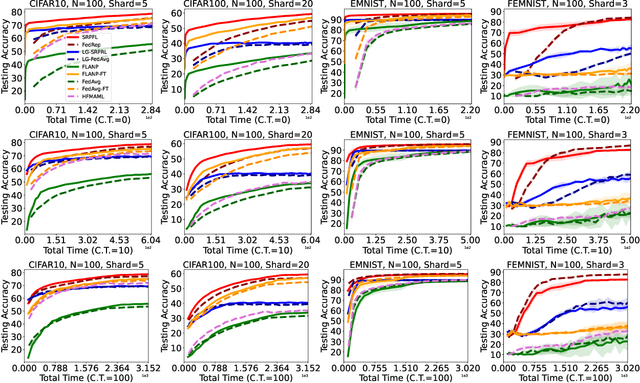
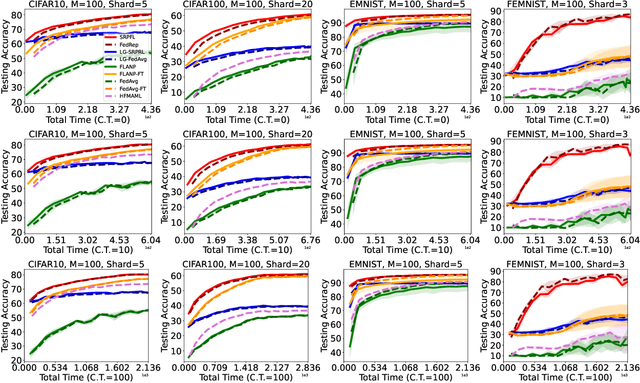
Federated Learning is an emerging learning paradigm that allows training models from samples distributed across a large network of clients while respecting privacy and communication restrictions. Despite its success, federated learning faces several challenges related to its decentralized nature. In this work, we develop a novel algorithmic procedure with theoretical speedup guarantees that simultaneously handles two of these hurdles, namely (i) data heterogeneity, i.e., data distributions can vary substantially across clients, and (ii) system heterogeneity, i.e., the computational power of the clients could differ significantly. Our method relies on ideas from representation learning theory to find a global common representation using all clients' data and learn a user-specific set of parameters leading to a personalized solution for each client. Furthermore, our method mitigates the effects of stragglers by adaptively selecting clients based on their computational characteristics and statistical significance, thus achieving, for the first time, near optimal sample complexity and provable logarithmic speedup. Experimental results support our theoretical findings showing the superiority of our method over alternative personalized federated schemes in system and data heterogeneous environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge