Robust Decentralized Learning with Local Updates and Gradient Tracking

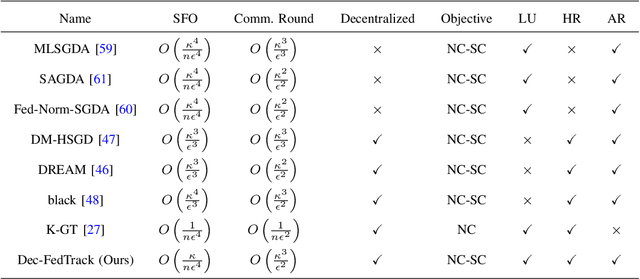
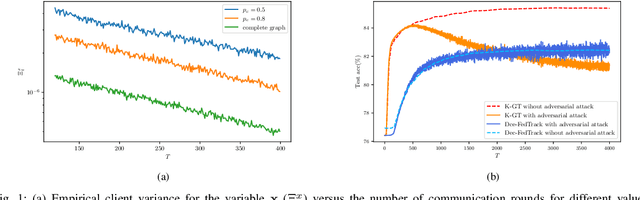
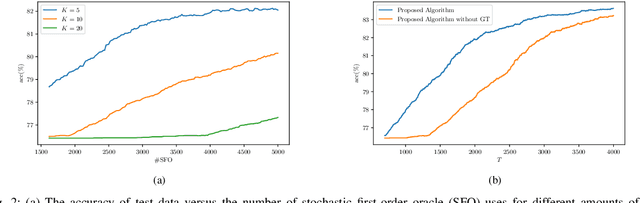
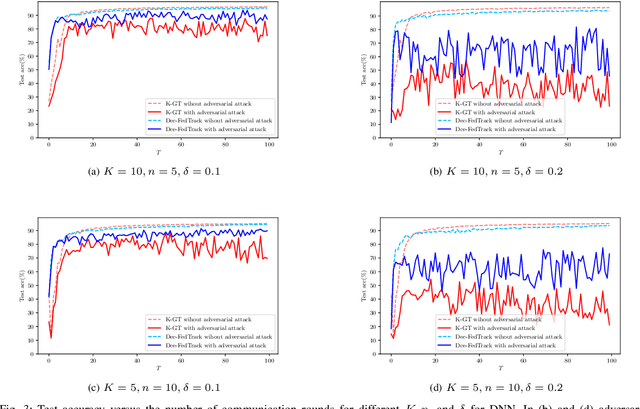
As distributed learning applications such as Federated Learning, the Internet of Things (IoT), and Edge Computing grow, it is critical to address the shortcomings of such technologies from a theoretical perspective. As an abstraction, we consider decentralized learning over a network of communicating clients or nodes and tackle two major challenges: data heterogeneity and adversarial robustness. We propose a decentralized minimax optimization method that employs two important modules: local updates and gradient tracking. Minimax optimization is the key tool to enable adversarial training for ensuring robustness. Having local updates is essential in Federated Learning (FL) applications to mitigate the communication bottleneck, and utilizing gradient tracking is essential to proving convergence in the case of data heterogeneity. We analyze the performance of the proposed algorithm, Dec-FedTrack, in the case of nonconvex-strongly concave minimax optimization, and prove that it converges a stationary point. We also conduct numerical experiments to support our theoretical findings.

EM for Mixture of Linear Regression with Clustered Data

Modern data-driven and distributed learning frameworks deal with diverse massive data generated by clients spread across heterogeneous environments. Indeed, data heterogeneity is a major bottleneck in scaling up many distributed learning paradigms. In many settings however, heterogeneous data may be generated in clusters with shared structures, as is the case in several applications such as federated learning where a common latent variable governs the distribution of all the samples generated by a client. It is therefore natural to ask how the underlying clustered structures in distributed data can be exploited to improve learning schemes. In this paper, we tackle this question in the special case of estimating $d$-dimensional parameters of a two-component mixture of linear regressions problem where each of $m$ nodes generates $n$ samples with a shared latent variable. We employ the well-known Expectation-Maximization (EM) method to estimate the maximum likelihood parameters from $m$ batches of dependent samples each containing $n$ measurements. Discarding the clustered structure in the mixture model, EM is known to require $O(\log(mn/d))$ iterations to reach the statistical accuracy of $O(\sqrt{d/(mn)})$. In contrast, we show that if initialized properly, EM on the structured data requires only $O(1)$ iterations to reach the same statistical accuracy, as long as $m$ grows up as $e^{o(n)}$. Our analysis establishes and combines novel asymptotic optimization and generalization guarantees for population and empirical EM with dependent samples, which may be of independent interest.

Variance-reduced Clipping for Non-convex Optimization

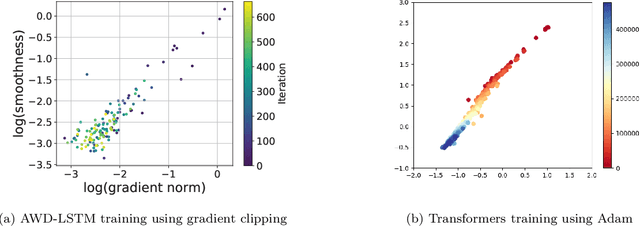
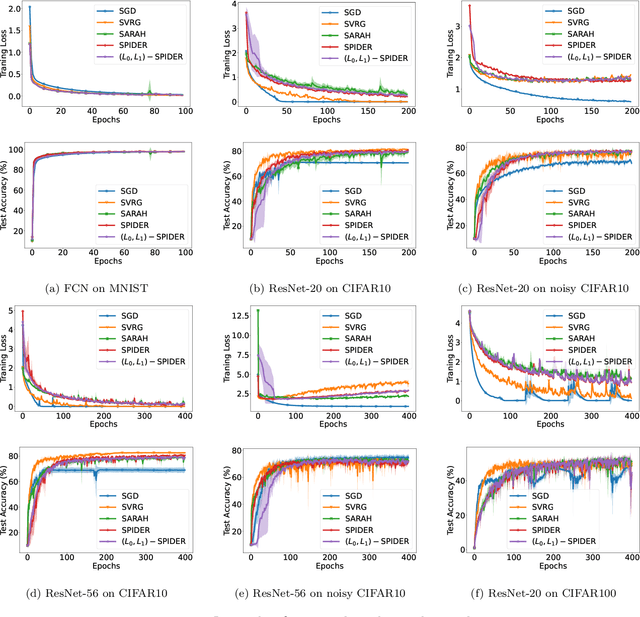
Gradient clipping is a standard training technique used in deep learning applications such as large-scale language modeling to mitigate exploding gradients. Recent experimental studies have demonstrated a fairly special behavior in the smoothness of the training objective along its trajectory when trained with gradient clipping. That is, the smoothness grows with the gradient norm. This is in clear contrast to the well-established assumption in folklore non-convex optimization, a.k.a. $L$-smoothness, where the smoothness is assumed to be bounded by a constant $L$ globally. The recently introduced $(L_0,L_1)$-smoothness is a more relaxed notion that captures such behavior in non-convex optimization. In particular, it has been shown that under this relaxed smoothness assumption, SGD with clipping requires $O(\epsilon^{-4})$ stochastic gradient computations to find an $\epsilon$-stationary solution. In this paper, we employ a variance reduction technique, namely SPIDER, and demonstrate that for a carefully designed learning rate, this complexity is improved to $O(\epsilon^{-3})$ which is order-optimal. The corresponding learning rate comprises the clipping technique to mitigate the growing smoothness. Moreover, when the objective function is the average of $n$ components, we improve the existing $O(n\epsilon^{-2})$ bound on the stochastic gradient complexity to order-optimal $O(\sqrt{n} \epsilon^{-2} + n)$.

Gradient Descent for Low-Rank Functions

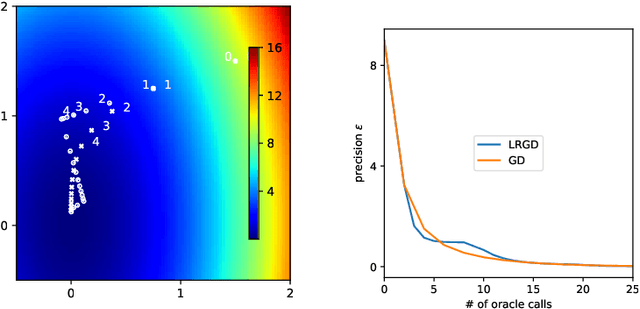
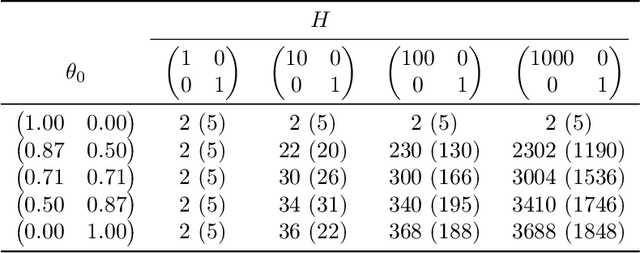
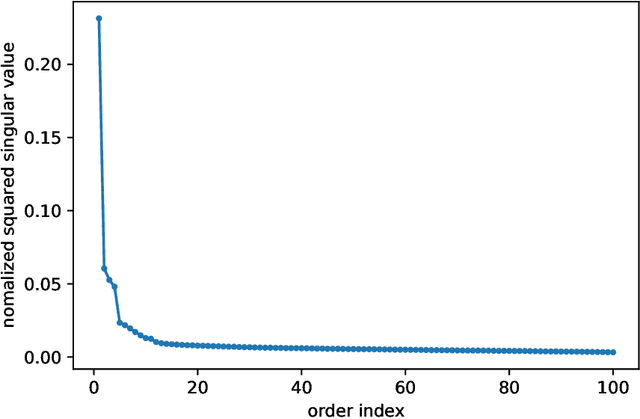
Several recent empirical studies demonstrate that important machine learning tasks, e.g., training deep neural networks, exhibit low-rank structure, where the loss function varies significantly in only a few directions of the input space. In this paper, we leverage such low-rank structure to reduce the high computational cost of canonical gradient-based methods such as gradient descent (GD). Our proposed \emph{Low-Rank Gradient Descent} (LRGD) algorithm finds an $\epsilon$-approximate stationary point of a $p$-dimensional function by first identifying $r \leq p$ significant directions, and then estimating the true $p$-dimensional gradient at every iteration by computing directional derivatives only along those $r$ directions. We establish that the "directional oracle complexities" of LRGD for strongly convex and non-convex objective functions are $\mathcal{O}(r \log(1/\epsilon) + rp)$ and $\mathcal{O}(r/\epsilon^2 + rp)$, respectively. When $r \ll p$, these complexities are smaller than the known complexities of $\mathcal{O}(p \log(1/\epsilon))$ and $\mathcal{O}(p/\epsilon^2)$ of {\gd} in the strongly convex and non-convex settings, respectively. Thus, LRGD significantly reduces the computational cost of gradient-based methods for sufficiently low-rank functions. In the course of our analysis, we also formally define and characterize the classes of exact and approximately low-rank functions.

An Optimal Transport Approach to Personalized Federated Learning

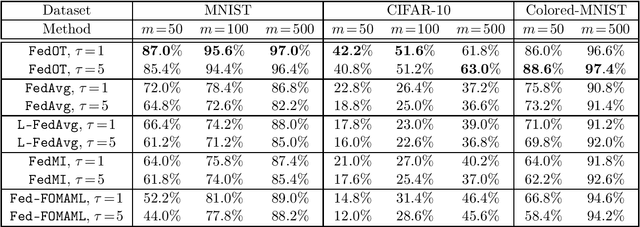
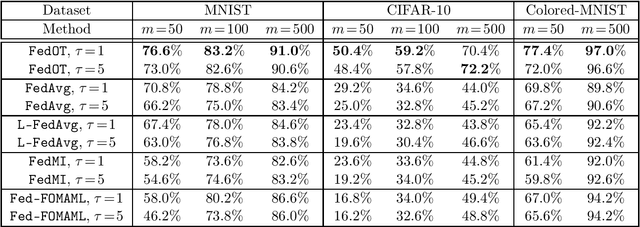
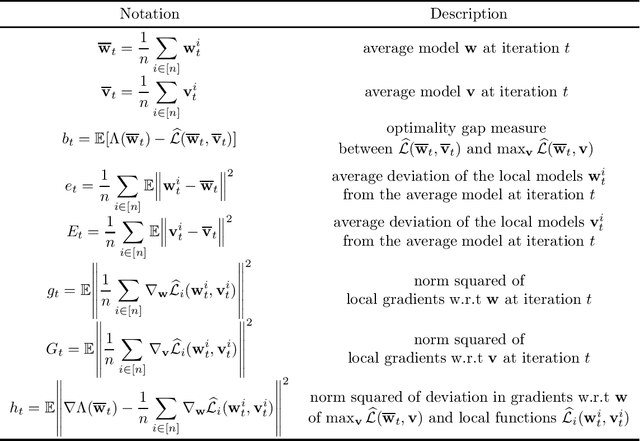
Federated learning is a distributed machine learning paradigm, which aims to train a model using the local data of many distributed clients. A key challenge in federated learning is that the data samples across the clients may not be identically distributed. To address this challenge, personalized federated learning with the goal of tailoring the learned model to the data distribution of every individual client has been proposed. In this paper, we focus on this problem and propose a novel personalized Federated Learning scheme based on Optimal Transport (FedOT) as a learning algorithm that learns the optimal transport maps for transferring data points to a common distribution as well as the prediction model under the applied transport map. To formulate the FedOT problem, we extend the standard optimal transport task between two probability distributions to multi-marginal optimal transport problems with the goal of transporting samples from multiple distributions to a common probability domain. We then leverage the results on multi-marginal optimal transport problems to formulate FedOT as a min-max optimization problem and analyze its generalization and optimization properties. We discuss the results of several numerical experiments to evaluate the performance of FedOT under heterogeneous data distributions in federated learning problems.

Straggler-Resilient Federated Learning: Leveraging the Interplay Between Statistical Accuracy and System Heterogeneity

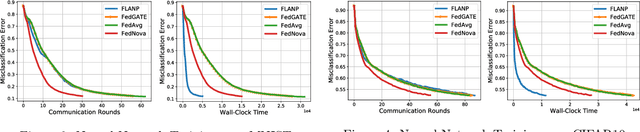
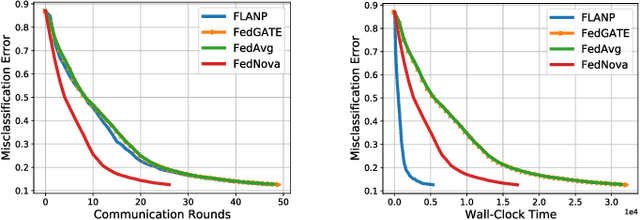
Federated Learning is a novel paradigm that involves learning from data samples distributed across a large network of clients while the data remains local. It is, however, known that federated learning is prone to multiple system challenges including system heterogeneity where clients have different computation and communication capabilities. Such heterogeneity in clients' computation speeds has a negative effect on the scalability of federated learning algorithms and causes significant slow-down in their runtime due to the existence of stragglers. In this paper, we propose a novel straggler-resilient federated learning method that incorporates statistical characteristics of the clients' data to adaptively select the clients in order to speed up the learning procedure. The key idea of our algorithm is to start the training procedure with faster nodes and gradually involve the slower nodes in the model training once the statistical accuracy of the data corresponding to the current participating nodes is reached. The proposed approach reduces the overall runtime required to achieve the statistical accuracy of data of all nodes, as the solution for each stage is close to the solution of the subsequent stage with more samples and can be used as a warm-start. Our theoretical results characterize the speedup gain in comparison to standard federated benchmarks for strongly convex objectives, and our numerical experiments also demonstrate significant speedups in wall-clock time of our straggler-resilient method compared to federated learning benchmarks.

Robust Federated Learning: The Case of Affine Distribution Shifts

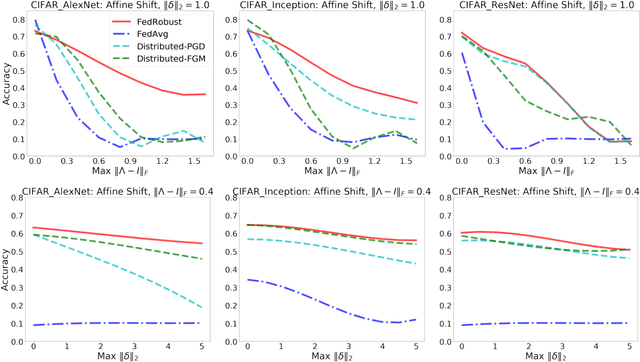
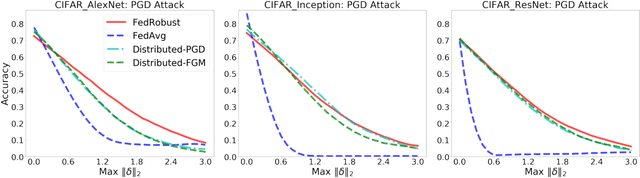
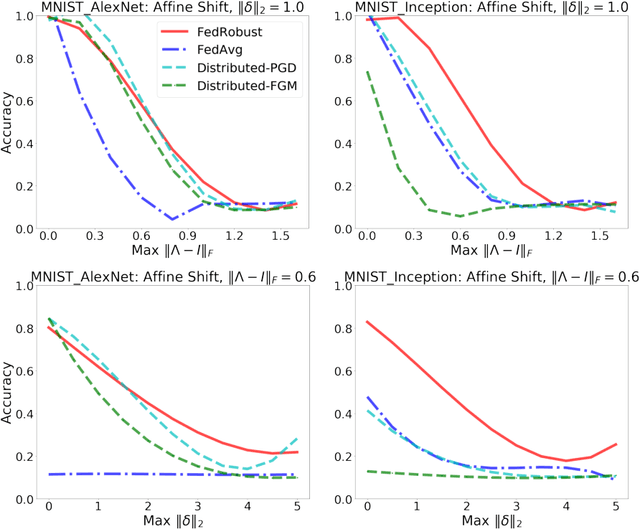
Federated learning is a distributed paradigm that aims at training models using samples distributed across multiple users in a network while keeping the samples on users' devices with the aim of efficiency and protecting users privacy. In such settings, the training data is often statistically heterogeneous and manifests various distribution shifts across users, which degrades the performance of the learnt model. The primary goal of this paper is to develop a robust federated learning algorithm that achieves satisfactory performance against distribution shifts in users' samples. To achieve this goal, we first consider a structured affine distribution shift in users' data that captures the device-dependent data heterogeneity in federated settings. This perturbation model is applicable to various federated learning problems such as image classification where the images undergo device-dependent imperfections, e.g. different intensity, contrast, and brightness. To address affine distribution shifts across users, we propose a Federated Learning framework Robust to Affine distribution shifts (FLRA) that is provably robust against affine Wasserstein shifts to the distribution of observed samples. To solve the FLRA's distributed minimax problem, we propose a fast and efficient optimization method and provide convergence guarantees via a gradient Descent Ascent (GDA) method. We further prove generalization error bounds for the learnt classifier to show proper generalization from empirical distribution of samples to the true underlying distribution. We perform several numerical experiments to empirically support FLRA. We show that an affine distribution shift indeed suffices to significantly decrease the performance of the learnt classifier in a new test user, and our proposed algorithm achieves a significant gain in comparison to standard federated learning and adversarial training methods.

FedPAQ: A Communication-Efficient Federated Learning Method with Periodic Averaging and Quantization

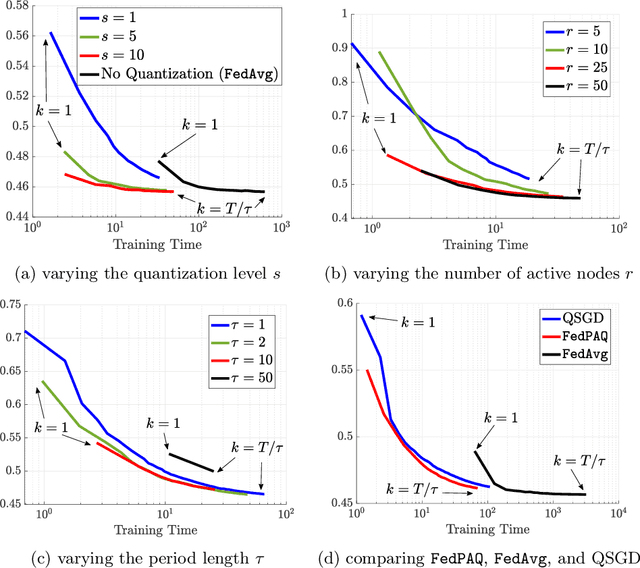
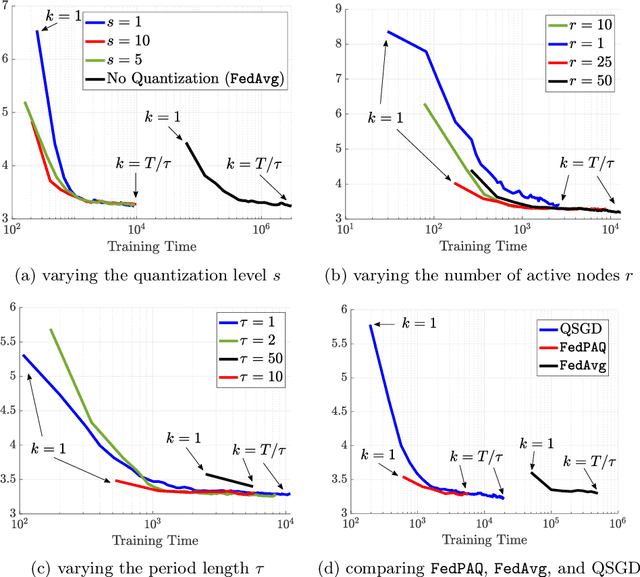
Federated learning is a distributed framework according to which a model is trained over a set of devices, while keeping data localized. This framework faces several systems-oriented challenges which include (i) communication bottleneck since a large number of devices upload their local updates to a parameter server, and (ii) scalability as the federated network consists of millions of devices. Due to these systems challenges as well as issues related to statistical heterogeneity of data and privacy concerns, designing a provably efficient federated learning method is of significant importance yet it remains challenging. In this paper, we present FedPAQ, a communication-efficient Federated Learning method with Periodic Averaging and Quantization. FedPAQ relies on three key features: (1) periodic averaging where models are updated locally at devices and only periodically averaged at the server; (2) partial device participation where only a fraction of devices participate in each round of the training; and (3) quantized message-passing where the edge nodes quantize their updates before uploading to the parameter server. These features address the communications and scalability challenges in federated learning. We also show that FedPAQ achieves near-optimal theoretical guarantees for strongly convex and non-convex loss functions and empirically demonstrate the communication-computation tradeoff provided by our method.

Robust and Communication-Efficient Collaborative Learning

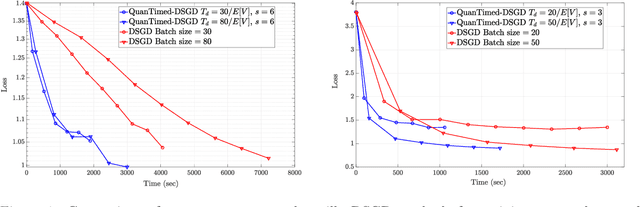
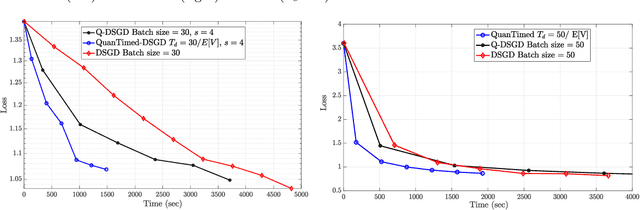
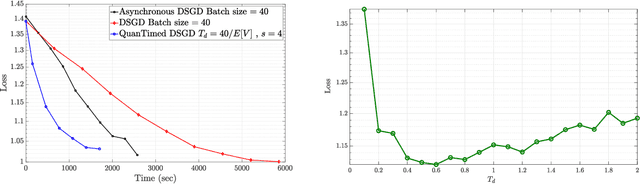
We consider a decentralized learning problem, where a set of computing nodes aim at solving a non-convex optimization problem collaboratively. It is well-known that decentralized optimization schemes face two major system bottlenecks: stragglers' delay and communication overhead. In this paper, we tackle these bottlenecks by proposing a novel decentralized and gradient-based optimization algorithm named as QuanTimed-DSGD. Our algorithm stands on two main ideas: (i) we impose a deadline on the local gradient computations of each node at each iteration of the algorithm, and (ii) the nodes exchange quantized versions of their local models. The first idea robustifies to straggling nodes and the second alleviates communication efficiency. The key technical contribution of our work is to prove that with non-vanishing noises for quantization and stochastic gradients, the proposed method exactly converges to the global optimal for convex loss functions, and finds a first-order stationary point in non-convex scenarios. Our numerical evaluations of the QuanTimed-DSGD on training benchmark datasets, MNIST and CIFAR-10, demonstrate speedups of up to 3x in run-time, compared to state-of-the-art decentralized optimization methods.

CodedReduce: A Fast and Robust Framework for Gradient Aggregation in Distributed Learning

We focus on the commonly used synchronous Gradient Descent paradigm for large-scale distributed learning, for which there has been a growing interest to develop efficient and robust gradient aggregation strategies that overcome two key bottlenecks: communication bandwidth and stragglers' delays. In particular, Ring-AllReduce (RAR) design has been proposed to avoid bandwidth bottleneck at any particular node by allowing each worker to only communicate with its neighbors that are arranged in a logical ring. On the other hand, Gradient Coding (GC) has been recently proposed to mitigate stragglers in a master-worker topology by allowing carefully designed redundant allocation of the data set to the workers. We propose a joint communication topology design and data set allocation strategy, named CodedReduce (CR), that combines the best of both RAR and GC. That is, it parallelizes the communications over a tree topology leading to efficient bandwidth utilization, and carefully designs a redundant data set allocation and coding strategy at the nodes to make the proposed gradient aggregation scheme robust to stragglers. In particular, we quantify the communication parallelization gain and resiliency of the proposed CR scheme, and prove its optimality when the communication topology is a regular tree. Furthermore, we empirically evaluate the performance of our proposed CR design over Amazon EC2 and demonstrate that it achieves speedups of up to 18.9x and 7.9x, respectively over the benchmarks GC and RAR.