Minimax Hypothesis Testing for the Bradley-Terry-Luce Model

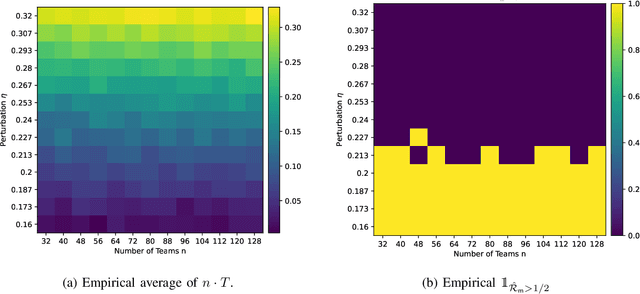
The Bradley-Terry-Luce (BTL) model is one of the most widely used models for ranking a collection of items or agents based on pairwise comparisons among them. Given $n$ agents, the BTL model endows each agent $i$ with a latent skill score $\alpha_i > 0$ and posits that the probability that agent $i$ is preferred over agent $j$ is $\alpha_i/(\alpha_i + \alpha_j)$. In this work, our objective is to formulate a hypothesis test that determines whether a given pairwise comparison dataset, with $k$ comparisons per pair of agents, originates from an underlying BTL model. We formalize this testing problem in the minimax sense and define the critical threshold of the problem. We then establish upper bounds on the critical threshold for general induced observation graphs (satisfying mild assumptions) and develop lower bounds for complete induced graphs. Our bounds demonstrate that for complete induced graphs, the critical threshold scales as $\Theta((nk)^{-1/2})$ in a minimax sense. In particular, our test statistic for the upper bounds is based on a new approximation we derive for the separation distance between general pairwise comparison models and the class of BTL models. To further assess the performance of our statistical test, we prove upper bounds on the type I and type II probabilities of error. Much of our analysis is conducted within the context of a fixed observation graph structure, where the graph possesses certain ``nice'' properties, such as expansion and bounded principal ratio. Additionally, we derive several auxiliary results, such as bounds on principal ratios of graphs, $\ell^2$-bounds on BTL parameter estimation under model mismatch, stability of rankings under the BTL model, etc. We validate our theoretical results through experiments on synthetic and real-world datasets and propose a data-driven permutation testing approach to determine test thresholds.

Gradient Descent for Low-Rank Functions

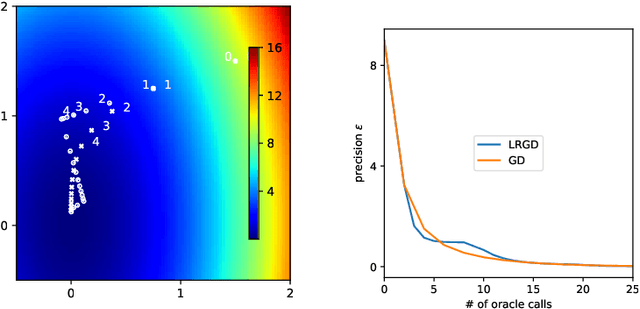
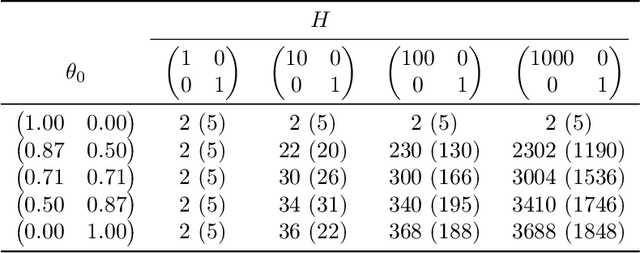
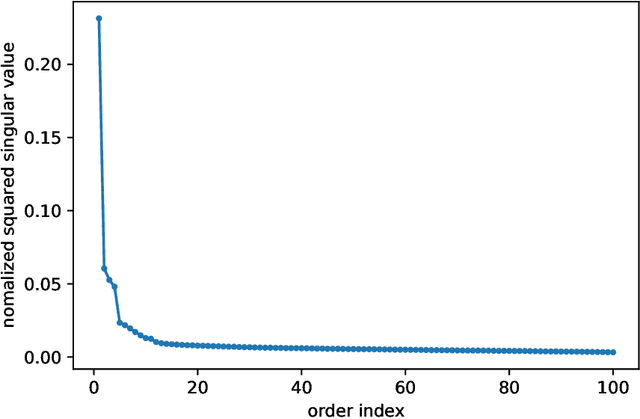
Several recent empirical studies demonstrate that important machine learning tasks, e.g., training deep neural networks, exhibit low-rank structure, where the loss function varies significantly in only a few directions of the input space. In this paper, we leverage such low-rank structure to reduce the high computational cost of canonical gradient-based methods such as gradient descent (GD). Our proposed \emph{Low-Rank Gradient Descent} (LRGD) algorithm finds an $\epsilon$-approximate stationary point of a $p$-dimensional function by first identifying $r \leq p$ significant directions, and then estimating the true $p$-dimensional gradient at every iteration by computing directional derivatives only along those $r$ directions. We establish that the "directional oracle complexities" of LRGD for strongly convex and non-convex objective functions are $\mathcal{O}(r \log(1/\epsilon) + rp)$ and $\mathcal{O}(r/\epsilon^2 + rp)$, respectively. When $r \ll p$, these complexities are smaller than the known complexities of $\mathcal{O}(p \log(1/\epsilon))$ and $\mathcal{O}(p/\epsilon^2)$ of {\gd} in the strongly convex and non-convex settings, respectively. Thus, LRGD significantly reduces the computational cost of gradient-based methods for sufficiently low-rank functions. In the course of our analysis, we also formally define and characterize the classes of exact and approximately low-rank functions.

Functional Linear Regression of CDFs

The estimation of cumulative distribution functions (CDF) is an important learning task with a great variety of downstream applications, e.g., risk assessments in predictions and decision making. We study functional regression of contextual CDFs where each data point is sampled from a linear combination of context dependent CDF bases. We propose estimation methods that estimate CDFs accurately everywhere. In particular, given $n$ samples with $d$ bases, we show estimation error upper bounds of $\widetilde O(\sqrt{d/n})$ for fixed design, random design, and adversarial context cases. We also derive matching information theoretic lower bounds, establishing minimax optimality for CDF functional regression. To complete our study, we consider agnostic settings where there is a mismatch in the data generation process. We characterize the error of the proposed estimator in terms of the mismatched error, and show that the estimator is well-behaved under model mismatch.

Federated Optimization of Smooth Loss Functions

In this work, we study empirical risk minimization (ERM) within a federated learning framework, where a central server minimizes an ERM objective function using training data that is stored across $m$ clients. In this setting, the Federated Averaging (FedAve) algorithm is the staple for determining $\epsilon$-approximate solutions to the ERM problem. Similar to standard optimization algorithms, the convergence analysis of FedAve only relies on smoothness of the loss function in the optimization parameter. However, loss functions are often very smooth in the training data too. To exploit this additional smoothness, we propose the Federated Low Rank Gradient Descent (FedLRGD) algorithm. Since smoothness in data induces an approximate low rank structure on the loss function, our method first performs a few rounds of communication between the server and clients to learn weights that the server can use to approximate clients' gradients. Then, our method solves the ERM problem at the server using inexact gradient descent. To show that FedLRGD can have superior performance to FedAve, we present a notion of federated oracle complexity as a counterpart to canonical oracle complexity. Under some assumptions on the loss function, e.g., strong convexity in parameter, $\eta$-H\"older smoothness in data, etc., we prove that the federated oracle complexity of FedLRGD scales like $\phi m(p/\epsilon)^{\Theta(d/\eta)}$ and that of FedAve scales like $\phi m(p/\epsilon)^{3/4}$ (neglecting sub-dominant factors), where $\phi\gg 1$ is a "communication-to-computation ratio," $p$ is the parameter dimension, and $d$ is the data dimension. Then, we show that when $d$ is small and the loss function is sufficiently smooth in the data, FedLRGD beats FedAve in federated oracle complexity. Finally, in the course of analyzing FedLRGD, we also establish a result on low rank approximation of latent variable models.

Gradient-Based Empirical Risk Minimization using Local Polynomial Regression

In this paper, we consider the problem of empirical risk minimization (ERM) of smooth, strongly convex loss functions using iterative gradient-based methods. A major goal of this literature has been to compare different algorithms, such as gradient descent (GD) or stochastic gradient descent (SGD), by analyzing their rates of convergence to $\epsilon$-approximate solutions. For example, the oracle complexity of GD is $O(n\log(\epsilon^{-1}))$, where $n$ is the number of training samples. When $n$ is large, this can be expensive in practice, and SGD is preferred due to its oracle complexity of $O(\epsilon^{-1})$. Such standard analyses only utilize the smoothness of the loss function in the parameter being optimized. In contrast, we demonstrate that when the loss function is smooth in the data, we can learn the oracle at every iteration and beat the oracle complexities of both GD and SGD in important regimes. Specifically, at every iteration, our proposed algorithm performs local polynomial regression to learn the gradient of the loss function, and then estimates the true gradient of the ERM objective function. We establish that the oracle complexity of our algorithm scales like $\tilde{O}((p \epsilon^{-1})^{d/(2\eta)})$ (neglecting sub-dominant factors), where $d$ and $p$ are the data and parameter space dimensions, respectively, and the gradient of the loss function belongs to a $\eta$-H\"{o}lder class with respect to the data. Our proof extends the analysis of local polynomial regression in non-parametric statistics to provide interpolation guarantees in multivariate settings, and also exploits tools from the inexact GD literature. Unlike GD and SGD, the complexity of our method depends on $d$ and $p$. However, when $d$ is small and the loss function exhibits modest smoothness in the data, our algorithm beats GD and SGD in oracle complexity for a very broad range of $p$ and $\epsilon$.

Estimation of Skill Distributions

In this paper, we study the problem of learning the skill distribution of a population of agents from observations of pairwise games in a tournament. These games are played among randomly drawn agents from the population. The agents in our model can be individuals, sports teams, or Wall Street fund managers. Formally, we postulate that the likelihoods of game outcomes are governed by the Bradley-Terry-Luce (or multinomial logit) model, where the probability of an agent beating another is the ratio between its skill level and the pairwise sum of skill levels, and the skill parameters are drawn from an unknown skill density of interest. The problem is, in essence, to learn a distribution from noisy, quantized observations. We propose a simple and tractable algorithm that learns the skill density with near-optimal minimax mean squared error scaling as $n^{-1+\varepsilon}$, for any $\varepsilon>0$, when the density is smooth. Our approach brings together prior work on learning skill parameters from pairwise comparisons with kernel density estimation from non-parametric statistics. Furthermore, we prove minimax lower bounds which establish minimax optimality of the skill parameter estimation technique used in our algorithm. These bounds utilize a continuum version of Fano's method along with a covering argument. We apply our algorithm to various soccer leagues and world cups, cricket world cups, and mutual funds. We find that the entropy of a learnt distribution provides a quantitative measure of skill, which provides rigorous explanations for popular beliefs about perceived qualities of sporting events, e.g., soccer league rankings. Finally, we apply our method to assess the skill distributions of mutual funds. Our results shed light on the abundance of low quality funds prior to the Great Recession of 2008, and the domination of the industry by more skilled funds after the financial crisis.

On Universal Features for High-Dimensional Learning and Inference

We consider the problem of identifying universal low-dimensional features from high-dimensional data for inference tasks in settings involving learning. For such problems, we introduce natural notions of universality and we show a local equivalence among them. Our analysis is naturally expressed via information geometry, and represents a conceptually and computationally useful analysis. The development reveals the complementary roles of the singular value decomposition, Hirschfeld-Gebelein-R\'enyi maximal correlation, the canonical correlation and principle component analyses of Hotelling and Pearson, Tishby's information bottleneck, Wyner's common information, Ky Fan $k$-norms, and Brieman and Friedman's alternating conditional expectations algorithm. We further illustrate how this framework facilitates understanding and optimizing aspects of learning systems, including multinomial logistic (softmax) regression and the associated neural network architecture, matrix factorization methods for collaborative filtering and other applications, rank-constrained multivariate linear regression, and forms of semi-supervised learning.

Probabilistic Clustering Using Maximal Matrix Norm Couplings

In this paper, we present a local information theoretic approach to explicitly learn probabilistic clustering of a discrete random variable. Our formulation yields a convex maximization problem for which it is NP-hard to find the global optimum. In order to algorithmically solve this optimization problem, we propose two relaxations that are solved via gradient ascent and alternating maximization. Experiments on the MSR Sentence Completion Challenge, MovieLens 100K, and Reuters21578 datasets demonstrate that our approach is competitive with existing techniques and worthy of further investigation.