The Pitfalls of Imitation Learning when Actions are Continuous

We study the problem of imitating an expert demonstrator in a discrete-time, continuous state-and-action control system. We show that, even if the dynamics are stable (i.e. contracting exponentially quickly), and the expert is smooth and deterministic, any smooth, deterministic imitator policy necessarily suffers error on execution that is exponentially larger, as a function of problem horizon, than the error under the distribution of expert training data. Our negative result applies to both behavior cloning and offline-RL algorithms, unless they produce highly "improper" imitator policies--those which are non-smooth, non-Markovian, or which exhibit highly state-dependent stochasticity--or unless the expert trajectory distribution is sufficiently "spread." We provide experimental evidence of the benefits of these more complex policy parameterizations, explicating the benefits of today's popular policy parameterizations in robot learning (e.g. action-chunking and Diffusion Policies). We also establish a host of complementary negative and positive results for imitation in control systems.

Fast Tensor Completion via Approximate Richardson Iteration

We study tensor completion (TC) through the lens of low-rank tensor decomposition (TD). Many TD algorithms use fast alternating minimization methods, which solve highly structured linear regression problems at each step (e.g., for CP, Tucker, and tensor-train decompositions). However, such algebraic structure is lost in TC regression problems, making direct extensions unclear. To address this, we propose a lifting approach that approximately solves TC regression problems using structured TD regression algorithms as blackbox subroutines, enabling sublinear-time methods. We theoretically analyze the convergence rate of our approximate Richardson iteration based algorithm, and we demonstrate on real-world tensors that its running time can be 100x faster than direct methods for CP completion.

On the Emergence of Position Bias in Transformers

Recent studies have revealed various manifestations of position bias in transformer architectures, from the "lost-in-the-middle" phenomenon to attention sinks, yet a comprehensive theoretical understanding of how attention masks and positional encodings shape these biases remains elusive. This paper introduces a novel graph-theoretic framework to analyze position bias in multi-layer attention. Modeling attention masks as directed graphs, we quantify how tokens interact with contextual information based on their sequential positions. We uncover two key insights: First, causal masking inherently biases attention toward earlier positions, as tokens in deeper layers attend to increasingly more contextualized representations of earlier tokens. Second, we characterize the competing effects of the causal mask and relative positional encodings, such as the decay mask and rotary positional encoding (RoPE): while both mechanisms introduce distance-based decay within individual attention maps, their aggregate effect across multiple attention layers -- coupled with the causal mask -- leads to a trade-off between the long-term decay effects and the cumulative importance of early sequence positions. Through controlled numerical experiments, we not only validate our theoretical findings but also reproduce position biases observed in real-world LLMs. Our framework offers a principled foundation for understanding positional biases in transformers, shedding light on the complex interplay of attention mechanism components and guiding more informed architectural design.

In-Context Learning of Polynomial Kernel Regression in Transformers with GLU Layers

Transformer-based models have demonstrated remarkable ability in in-context learning (ICL), where they can adapt to unseen tasks from a prompt with a few examples, without requiring parameter updates. Recent research has provided insight into how linear Transformers can perform ICL by implementing gradient descent estimators. In particular, it has been shown that the optimal linear self-attention (LSA) mechanism can implement one step of gradient descent with respect to a linear least-squares objective when trained on random linear regression tasks. However, the theoretical understanding of ICL for nonlinear function classes remains limited. In this work, we address this gap by first showing that LSA is inherently restricted to solving linear least-squares objectives and thus, the solutions in prior works cannot readily extend to nonlinear ICL tasks. To overcome this limitation, drawing inspiration from modern architectures, we study a mechanism that combines LSA with GLU-like feed-forward layers and show that this allows the model to perform one step of gradient descent on a polynomial kernel regression. Further, we characterize the scaling behavior of the resulting Transformer model, highlighting the necessary model size to effectively handle quadratic ICL tasks. Our findings highlight the distinct roles of attention and feed-forward layers in nonlinear ICL and identify key challenges when extending ICL to nonlinear function classes.

GraphHash: Graph Clustering Enables Parameter Efficiency in Recommender Systems

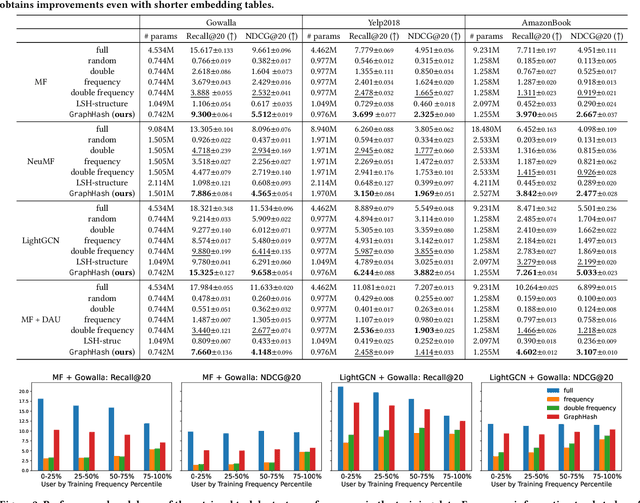
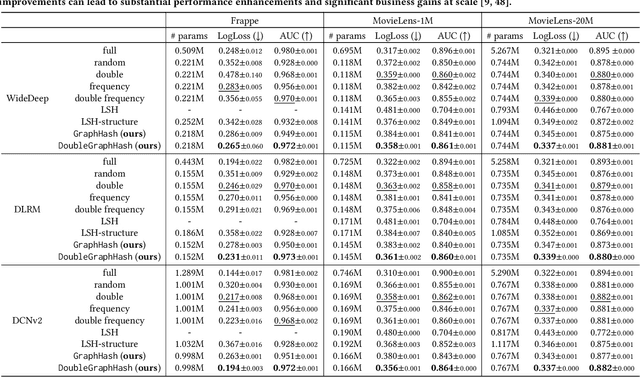
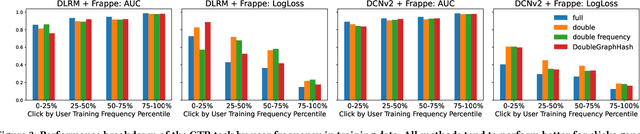
Deep recommender systems rely heavily on large embedding tables to handle high-cardinality categorical features such as user/item identifiers, and face significant memory constraints at scale. To tackle this challenge, hashing techniques are often employed to map multiple entities to the same embedding and thus reduce the size of the embedding tables. Concurrently, graph-based collaborative signals have emerged as powerful tools in recommender systems, yet their potential for optimizing embedding table reduction remains unexplored. This paper introduces GraphHash, the first graph-based approach that leverages modularity-based bipartite graph clustering on user-item interaction graphs to reduce embedding table sizes. We demonstrate that the modularity objective has a theoretical connection to message-passing, which provides a foundation for our method. By employing fast clustering algorithms, GraphHash serves as a computationally efficient proxy for message-passing during preprocessing and a plug-and-play graph-based alternative to traditional ID hashing. Extensive experiments show that GraphHash substantially outperforms diverse hashing baselines on both retrieval and click-through-rate prediction tasks. In particular, GraphHash achieves on average a 101.52% improvement in recall when reducing the embedding table size by more than 75%, highlighting the value of graph-based collaborative information for model reduction.

Improved Sample Complexity of Imitation Learning for Barrier Model Predictive Control

Recent work in imitation learning has shown that having an expert controller that is both suitably smooth and stable enables stronger guarantees on the performance of the learned controller. However, constructing such smoothed expert controllers for arbitrary systems remains challenging, especially in the presence of input and state constraints. As our primary contribution, we show how such a smoothed expert can be designed for a general class of systems using a log-barrier-based relaxation of a standard Model Predictive Control (MPC) optimization problem. Improving upon our previous work, we show that barrier MPC achieves theoretically optimal error-to-smoothness tradeoff along some direction. At the core of this theoretical guarantee on smoothness is an improved lower bound we prove on the optimality gap of the analytic center associated with a convex Lipschitz function, which we believe could be of independent interest. We validate our theoretical findings via experiments, demonstrating the merits of our smoothing approach over randomized smoothing.

Residual Connections and Normalization Can Provably Prevent Oversmoothing in GNNs

Residual connections and normalization layers have become standard design choices for graph neural networks (GNNs), and were proposed as solutions to the mitigate the oversmoothing problem in GNNs. However, how exactly these methods help alleviate the oversmoothing problem from a theoretical perspective is not well understood. In this work, we provide a formal and precise characterization of (linearized) GNNs with residual connections and normalization layers. We establish that (a) for residual connections, the incorporation of the initial features at each layer can prevent the signal from becoming too smooth, and determines the subspace of possible node representations; (b) batch normalization prevents a complete collapse of the output embedding space to a one-dimensional subspace through the individual rescaling of each column of the feature matrix. This results in the convergence of node representations to the top-$k$ eigenspace of the message-passing operator; (c) moreover, we show that the centering step of a normalization layer -- which can be understood as a projection -- alters the graph signal in message-passing in such a way that relevant information can become harder to extract. We therefore introduce a novel, principled normalization layer called GraphNormv2 in which the centering step is learned such that it does not distort the original graph signal in an undesirable way. Experimental results confirm the effectiveness of our method.

On the Role of Attention Masks and LayerNorm in Transformers

Self-attention is the key mechanism of transformers, which are the essential building blocks of modern foundation models. Recent studies have shown that pure self-attention suffers from an increasing degree of rank collapse as depth increases, limiting model expressivity and further utilization of model depth. The existing literature on rank collapse, however, has mostly overlooked other critical components in transformers that may alleviate the rank collapse issue. In this paper, we provide a general analysis of rank collapse under self-attention, taking into account the effects of attention masks and layer normalization (LayerNorm). In particular, we find that although pure masked attention still suffers from exponential collapse to a rank one subspace, local masked attention can provably slow down the collapse rate. In the case of self-attention with LayerNorm, we first show that for certain classes of value matrices, collapse to a rank one subspace still happens exponentially. However, through construction of nontrivial counterexamples, we then establish that with proper choice of value matrices, a general class of sequences may not converge to a rank one subspace, and the self-attention dynamics with LayerNorm can simultaneously possess a rich set of equilibria with any possible rank between one and full. Our result refutes the previous hypothesis that LayerNorm plays no role in the rank collapse of self-attention and suggests that self-attention with LayerNorm constitutes a much more expressive, versatile nonlinear dynamical system than what was originally thought.

A least-square method for non-asymptotic identification in linear switching control

The focus of this paper is on linear system identification in the setting where it is known that the underlying partially-observed linear dynamical system lies within a finite collection of known candidate models. We first consider the problem of identification from a given trajectory, which in this setting reduces to identifying the index of the true model with high probability. We characterize the finite-time sample complexity of this problem by leveraging recent advances in the non-asymptotic analysis of linear least-square methods in the literature. In comparison to the earlier results that assume no prior knowledge of the system, our approach takes advantage of the smaller hypothesis class and leads to the design of a learner with a dimension-free sample complexity bound. Next, we consider the switching control of linear systems, where there is a candidate controller for each of the candidate models and data is collected through interaction of the system with a collection of potentially destabilizing controllers. We develop a dimension-dependent criterion that can detect those destabilizing controllers in finite time. By leveraging these results, we propose a data-driven switching strategy that identifies the unknown parameters of the underlying system. We then provide a non-asymptotic analysis of its performance and discuss its implications on the classical method of estimator-based supervisory control.

Belief Samples Are All You Need For Social Learning

In this paper, we consider the problem of social learning, where a group of agents embedded in a social network are interested in learning an underlying state of the world. Agents have incomplete, noisy, and heterogeneous sources of information, providing them with recurring private observations of the underlying state of the world. Agents can share their learning experience with their peers by taking actions observable to them, with values from a finite feasible set of states. Actions can be interpreted as samples from the beliefs which agents may form and update on what the true state of the world is. Sharing samples, in place of full beliefs, is motivated by the limited communication, cognitive, and information-processing resources available to agents especially in large populations. Previous work (Salhab et al.) poses the question as to whether learning with probability one is still achievable if agents are only allowed to communicate samples from their beliefs. We provide a definite positive answer to this question, assuming a strongly connected network and a ``collective distinguishability'' assumption, which are both required for learning even in full-belief-sharing settings. In our proposed belief update mechanism, each agent's belief is a normalized weighted geometric interpolation between a fully Bayesian private belief -- aggregating information from the private source -- and an ensemble of empirical distributions of the samples shared by her neighbors over time. By carefully constructing asymptotic almost-sure lower/upper bounds on the frequency of shared samples matching the true state/or not, we rigorously prove the convergence of all the beliefs to the true state, with probability one.