Residual Connections and Normalization Can Provably Prevent Oversmoothing in GNNs

Residual connections and normalization layers have become standard design choices for graph neural networks (GNNs), and were proposed as solutions to the mitigate the oversmoothing problem in GNNs. However, how exactly these methods help alleviate the oversmoothing problem from a theoretical perspective is not well understood. In this work, we provide a formal and precise characterization of (linearized) GNNs with residual connections and normalization layers. We establish that (a) for residual connections, the incorporation of the initial features at each layer can prevent the signal from becoming too smooth, and determines the subspace of possible node representations; (b) batch normalization prevents a complete collapse of the output embedding space to a one-dimensional subspace through the individual rescaling of each column of the feature matrix. This results in the convergence of node representations to the top-$k$ eigenspace of the message-passing operator; (c) moreover, we show that the centering step of a normalization layer -- which can be understood as a projection -- alters the graph signal in message-passing in such a way that relevant information can become harder to extract. We therefore introduce a novel, principled normalization layer called GraphNormv2 in which the centering step is learned such that it does not distort the original graph signal in an undesirable way. Experimental results confirm the effectiveness of our method.

ICML 2023 Topological Deep Learning Challenge : Design and Results

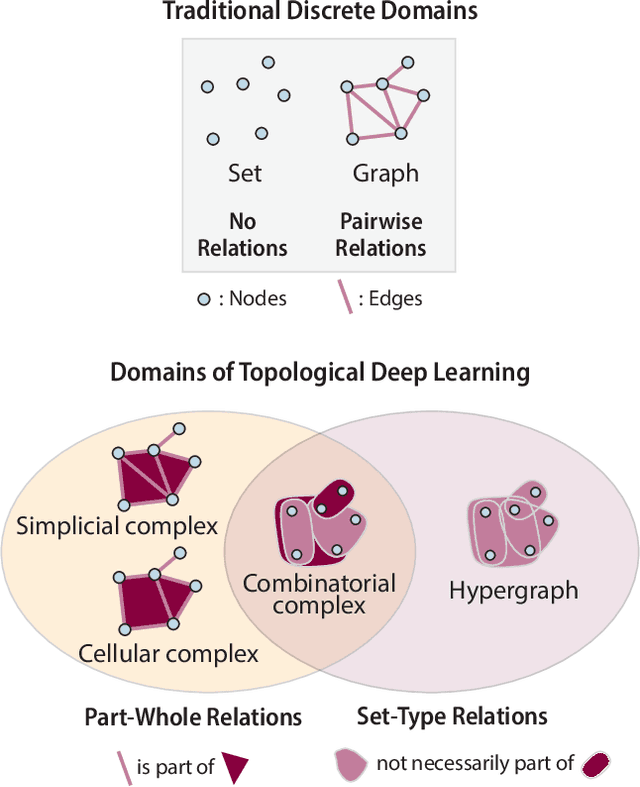
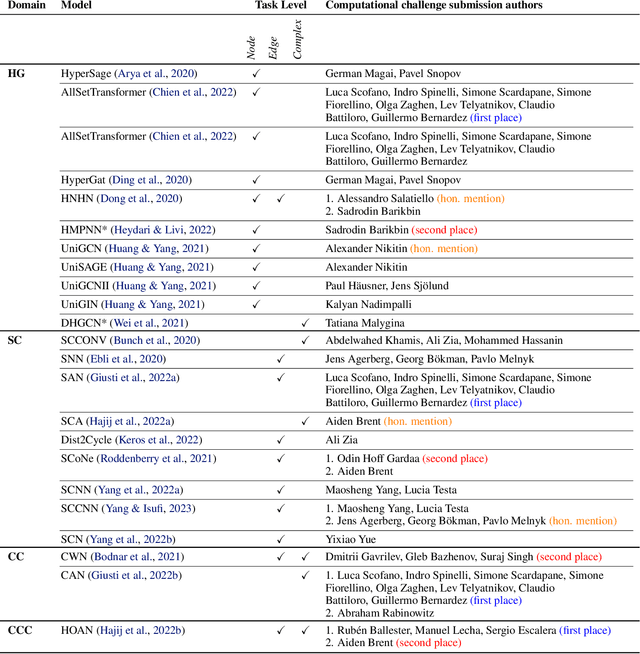
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.

Learning the effective order of a hypergraph dynamical system

Dynamical systems on hypergraphs can display a rich set of behaviours not observable for systems with pairwise interactions. Given a distributed dynamical system with a putative hypergraph structure, an interesting question is thus how much of this hypergraph structure is actually necessary to faithfully replicate the observed dynamical behaviour. To answer this question, we propose a method to determine the minimum order of a hypergraph necessary to approximate the corresponding dynamics accurately. Specifically, we develop an analytical framework that allows us to determine this order when the type of dynamics is known. We utilize these ideas in conjunction with a hypergraph neural network to directly learn the dynamics itself and the resulting order of the hypergraph from both synthetic and real data sets consisting of observed system trajectories.

Blind Extraction of Equitable Partitions from Graph Signals

Finding equitable partitions is closely related to the extraction of graph symmetries and of interest in a variety of applications context such as node role detection, cluster synchronization, consensus dynamics, and network control problems. In this work we study a blind identification problem in which we aim to recover an equitable partition of a network without the knowledge of the network's edges but based solely on the observations of the outputs of an unknown graph filter. Specifically, we consider two settings. First, we consider a scenario in which we can control the input to the graph filter and present a method to extract the partition inspired by the well known Weisfeiler-Lehman (color refinement) algorithm. Second, we generalize this idea to a setting where only observe the outputs to random, low-rank excitations of the graph filter, and present a simple spectral algorithm to extract the relevant equitable partitions. Finally, we establish theoretical bounds on the error that this spectral detection scheme incurs and perform numerical experiments that illustrate our theoretical results and compare both algorithms.

Local, global and scale-dependent node roles

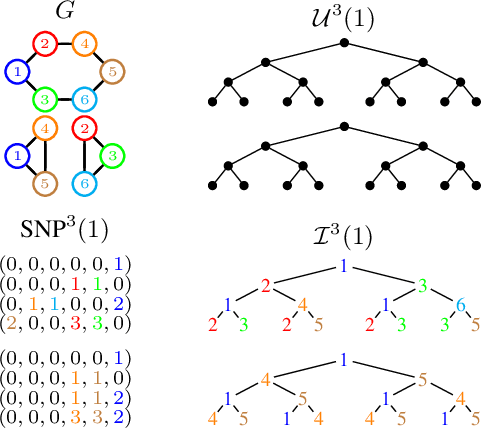
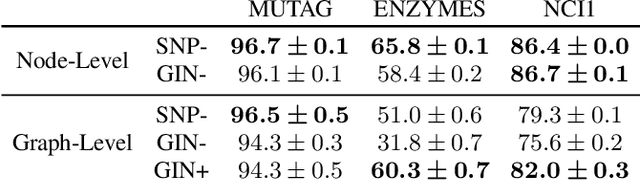
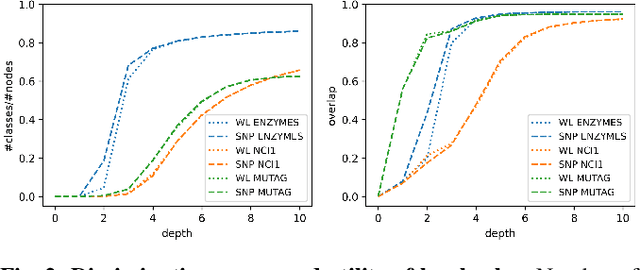
This paper re-examines the concept of node equivalences like structural equivalence or automorphic equivalence, which have originally emerged in social network analysis to characterize the role an actor plays within a social system, but have since then been of independent interest for graph-based learning tasks. Traditionally, such exact node equivalences have been defined either in terms of the one hop neighborhood of a node, or in terms of the global graph structure. Here we formalize exact node roles with a scale-parameter, describing up to what distance the ego network of a node should be considered when assigning node roles - motivated by the idea that there can be local roles of a node that should not be determined by nodes arbitrarily far away in the network. We present numerical experiments that show how already "shallow" roles of depth 3 or 4 carry sufficient information to perform node classification tasks with high accuracy. These findings corroborate the success of recent graph-learning approaches that compute approximate node roles in terms of embeddings, by nonlinearly aggregating node features in an (un)supervised manner over relatively small neighborhood sizes. Indeed, based on our ideas we can construct a shallow classifier achieving on par results with recent graph neural network architectures.