Entropic Analysis of Time Series through Kernel Density Estimation

This work presents a novel framework for time series analysis using entropic measures based on the kernel density estimate (KDE) of the time series' Takens' embeddings. Using this framework we introduce two distinct analytical tools: (1) a multi-scale KDE entropy metric, denoted as $\Delta\text{KE}$, which quantifies the evolution of time series complexity across different scales by measuring certain entropy changes, and (2) a sliding baseline method that employs the Kullback-Leibler (KL) divergence to detect changes in time series dynamics through changes in KDEs. The $\Delta{\rm KE}$ metric offers insights into the information content and ``unfolding'' properties of the time series' embedding related to dynamical systems, while the KL divergence-based approach provides a noise and outlier robust approach for identifying time series change points (injections in RF signals, e.g.). We demonstrate the versatility and effectiveness of these tools through a set of experiments encompassing diverse domains. In the space of radio frequency (RF) signal processing, we achieve accurate detection of signal injections under varying noise and interference conditions. Furthermore, we apply our methodology to electrocardiography (ECG) data, successfully identifying instances of ventricular fibrillation with high accuracy. Finally, we demonstrate the potential of our tools for dynamic state detection by accurately identifying chaotic regimes within an intermittent signal. These results show the broad applicability of our framework for extracting meaningful insights from complex time series data across various scientific disciplines.

Talking to GDELT Through Knowledge Graphs

In this work we study various Retrieval Augmented Regeneration (RAG) approaches to gain an understanding of the strengths and weaknesses of each approach in a question-answering analysis. To gain this understanding we use a case-study subset of the Global Database of Events, Language, and Tone (GDELT) dataset as well as a corpus of raw text scraped from the online news articles. To retrieve information from the text corpus we implement a traditional vector store RAG as well as state-of-the-art large language model (LLM) based approaches for automatically constructing KGs and retrieving the relevant subgraphs. In addition to these corpus approaches, we develop a novel ontology-based framework for constructing knowledge graphs (KGs) from GDELT directly which leverages the underlying schema of GDELT to create structured representations of global events. For retrieving relevant information from the ontology-based KGs we implement both direct graph queries and state-of-the-art graph retrieval approaches. We compare the performance of each method in a question-answering task. We find that while our ontology-based KGs are valuable for question-answering, automated extraction of the relevant subgraphs is challenging. Conversely, LLM-generated KGs, while capturing event summaries, often lack consistency and interpretability. Our findings suggest benefits of a synergistic approach between ontology and LLM-based KG construction, with proposed avenues toward that end.

ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

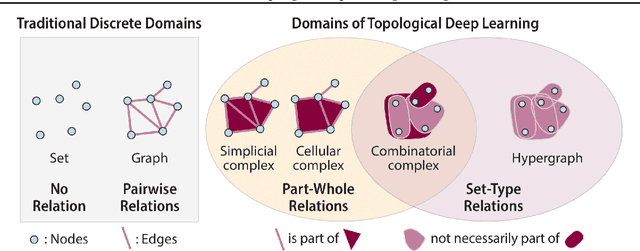
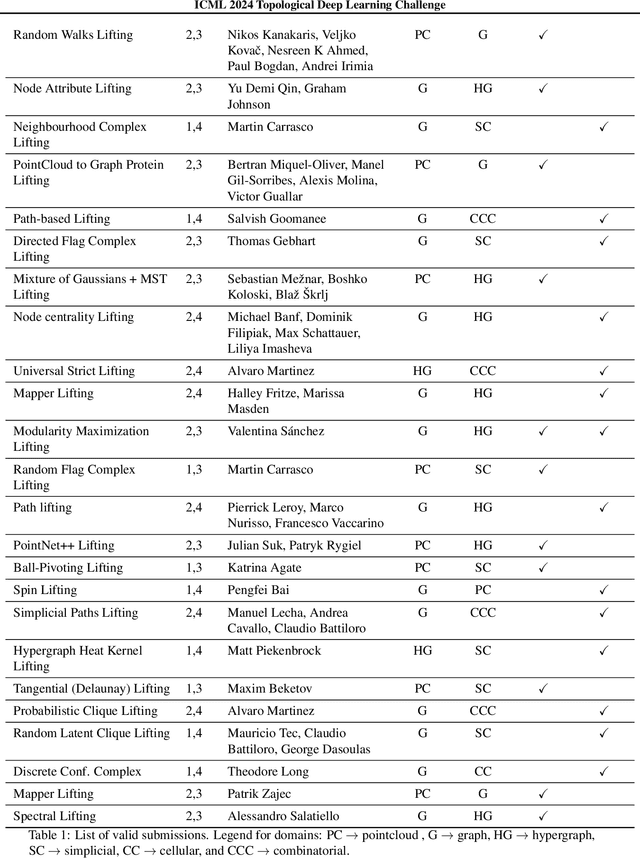
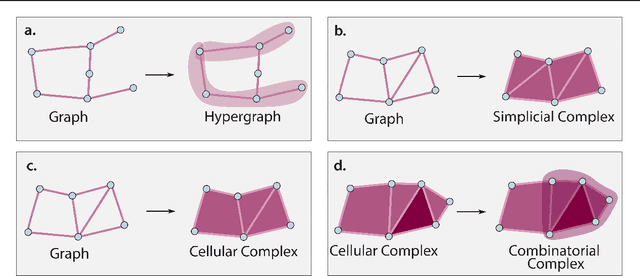
This paper describes the 2nd edition of the ICML Topological Deep Learning Challenge that was hosted within the ICML 2024 ELLIS Workshop on Geometry-grounded Representation Learning and Generative Modeling (GRaM). The challenge focused on the problem of representing data in different discrete topological domains in order to bridge the gap between Topological Deep Learning (TDL) and other types of structured datasets (e.g. point clouds, graphs). Specifically, participants were asked to design and implement topological liftings, i.e. mappings between different data structures and topological domains --like hypergraphs, or simplicial/cell/combinatorial complexes. The challenge received 52 submissions satisfying all the requirements. This paper introduces the main scope of the challenge, and summarizes the main results and findings.

ICML 2023 Topological Deep Learning Challenge : Design and Results

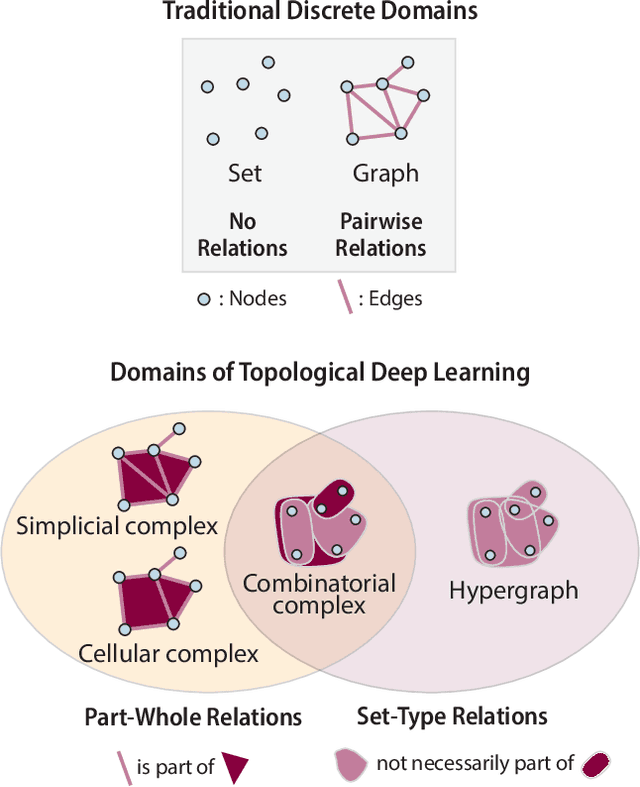
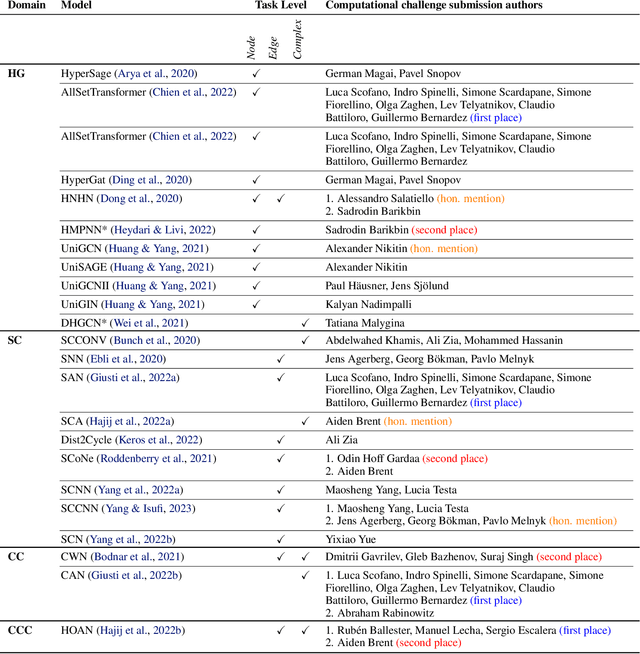
This paper presents the computational challenge on topological deep learning that was hosted within the ICML 2023 Workshop on Topology and Geometry in Machine Learning. The competition asked participants to provide open-source implementations of topological neural networks from the literature by contributing to the python packages TopoNetX (data processing) and TopoModelX (deep learning). The challenge attracted twenty-eight qualifying submissions in its two-month duration. This paper describes the design of the challenge and summarizes its main findings.