Talking to GDELT Through Knowledge Graphs

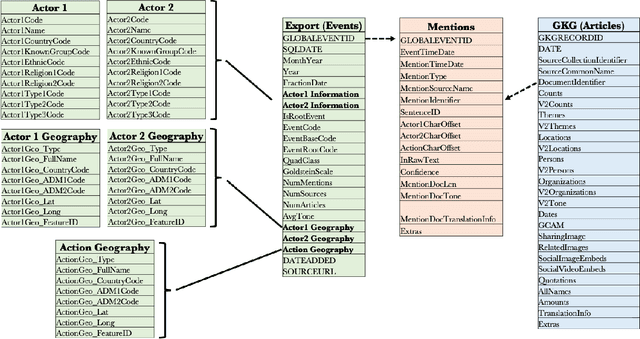
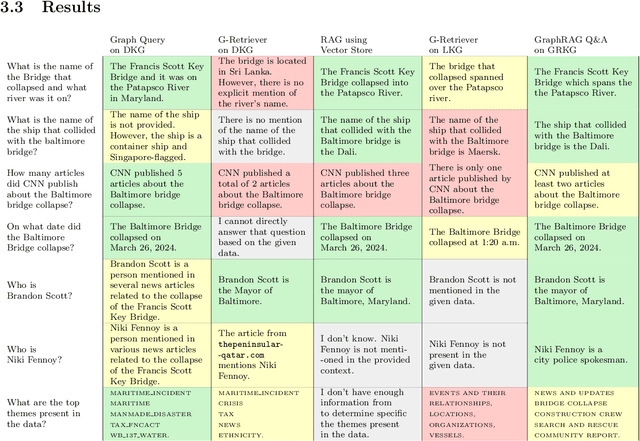
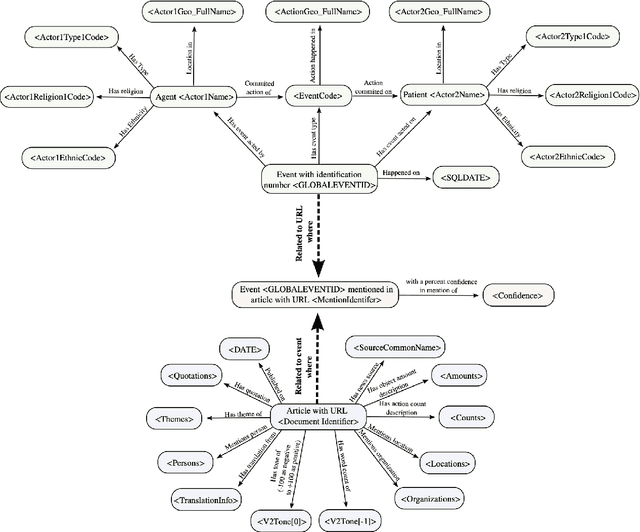
In this work we study various Retrieval Augmented Regeneration (RAG) approaches to gain an understanding of the strengths and weaknesses of each approach in a question-answering analysis. To gain this understanding we use a case-study subset of the Global Database of Events, Language, and Tone (GDELT) dataset as well as a corpus of raw text scraped from the online news articles. To retrieve information from the text corpus we implement a traditional vector store RAG as well as state-of-the-art large language model (LLM) based approaches for automatically constructing KGs and retrieving the relevant subgraphs. In addition to these corpus approaches, we develop a novel ontology-based framework for constructing knowledge graphs (KGs) from GDELT directly which leverages the underlying schema of GDELT to create structured representations of global events. For retrieving relevant information from the ontology-based KGs we implement both direct graph queries and state-of-the-art graph retrieval approaches. We compare the performance of each method in a question-answering task. We find that while our ontology-based KGs are valuable for question-answering, automated extraction of the relevant subgraphs is challenging. Conversely, LLM-generated KGs, while capturing event summaries, often lack consistency and interpretability. Our findings suggest benefits of a synergistic approach between ontology and LLM-based KG construction, with proposed avenues toward that end.

Experimental Observations of the Topology of Convolutional Neural Network Activations

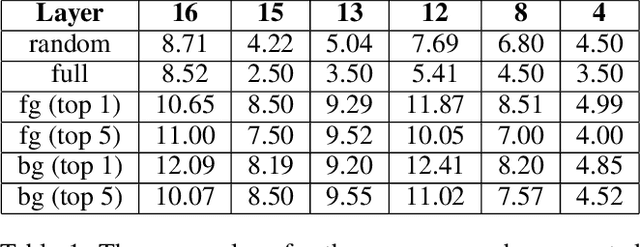
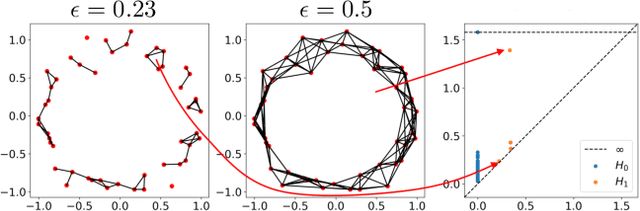
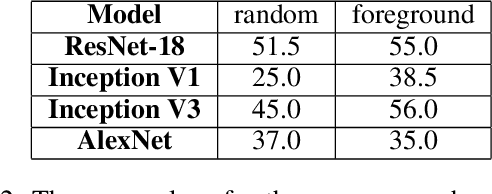
Topological data analysis (TDA) is a branch of computational mathematics, bridging algebraic topology and data science, that provides compact, noise-robust representations of complex structures. Deep neural networks (DNNs) learn millions of parameters associated with a series of transformations defined by the model architecture, resulting in high-dimensional, difficult-to-interpret internal representations of input data. As DNNs become more ubiquitous across multiple sectors of our society, there is increasing recognition that mathematical methods are needed to aid analysts, researchers, and practitioners in understanding and interpreting how these models' internal representations relate to the final classification. In this paper, we apply cutting edge techniques from TDA with the goal of gaining insight into the interpretability of convolutional neural networks used for image classification. We use two common TDA approaches to explore several methods for modeling hidden-layer activations as high-dimensional point clouds, and provide experimental evidence that these point clouds capture valuable structural information about the model's process. First, we demonstrate that a distance metric based on persistent homology can be used to quantify meaningful differences between layers, and we discuss these distances in the broader context of existing representational similarity metrics for neural network interpretability. Second, we show that a mapper graph can provide semantic insight into how these models organize hierarchical class knowledge at each layer. These observations demonstrate that TDA is a useful tool to help deep learning practitioners unlock the hidden structures of their models.

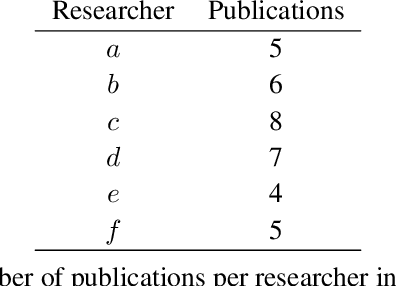
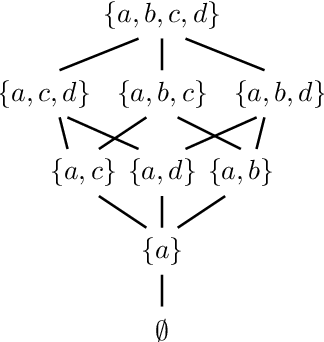
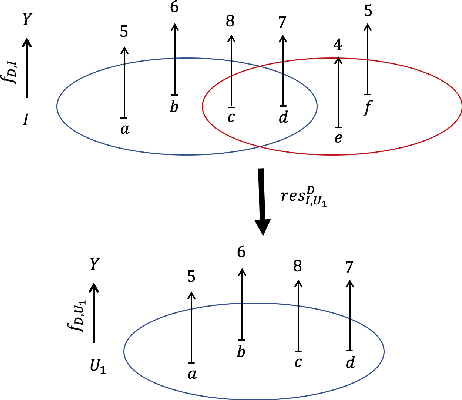
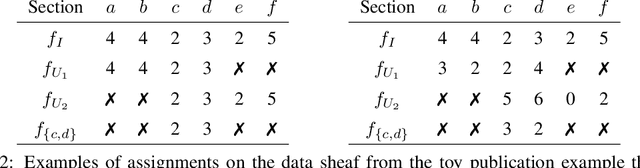
Sheaves as a Framework for Understanding and Interpreting Model Fit

As data grows in size and complexity, finding frameworks which aid in interpretation and analysis has become critical. This is particularly true when data comes from complex systems where extensive structure is available, but must be drawn from peripheral sources. In this paper we argue that in such situations, sheaves can provide a natural framework to analyze how well a statistical model fits at the local level (that is, on subsets of related datapoints) vs the global level (on all the data). The sheaf-based approach that we propose is suitably general enough to be useful in a range of applications, from analyzing sensor networks to understanding the feature space of a deep learning model.