Brenda Praggastis
Experimental Observations of the Topology of Convolutional Neural Network Activations
Dec 01, 2022
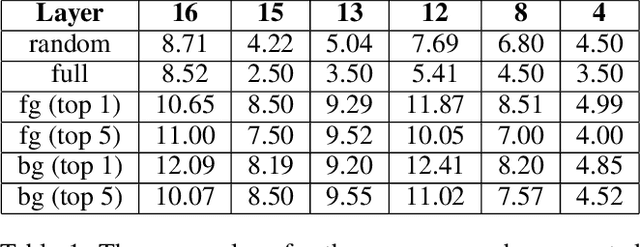
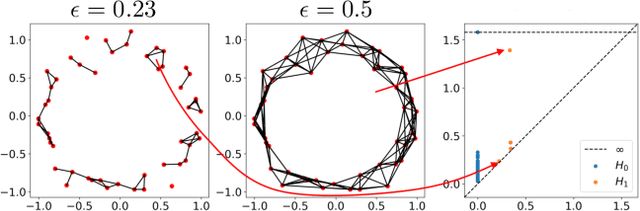
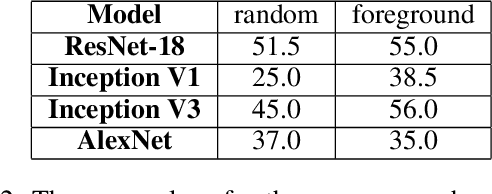
Abstract:Topological data analysis (TDA) is a branch of computational mathematics, bridging algebraic topology and data science, that provides compact, noise-robust representations of complex structures. Deep neural networks (DNNs) learn millions of parameters associated with a series of transformations defined by the model architecture, resulting in high-dimensional, difficult-to-interpret internal representations of input data. As DNNs become more ubiquitous across multiple sectors of our society, there is increasing recognition that mathematical methods are needed to aid analysts, researchers, and practitioners in understanding and interpreting how these models' internal representations relate to the final classification. In this paper, we apply cutting edge techniques from TDA with the goal of gaining insight into the interpretability of convolutional neural networks used for image classification. We use two common TDA approaches to explore several methods for modeling hidden-layer activations as high-dimensional point clouds, and provide experimental evidence that these point clouds capture valuable structural information about the model's process. First, we demonstrate that a distance metric based on persistent homology can be used to quantify meaningful differences between layers, and we discuss these distances in the broader context of existing representational similarity metrics for neural network interpretability. Second, we show that a mapper graph can provide semantic insight into how these models organize hierarchical class knowledge at each layer. These observations demonstrate that TDA is a useful tool to help deep learning practitioners unlock the hidden structures of their models.
The SVD of Convolutional Weights: A CNN Interpretability Framework
Aug 14, 2022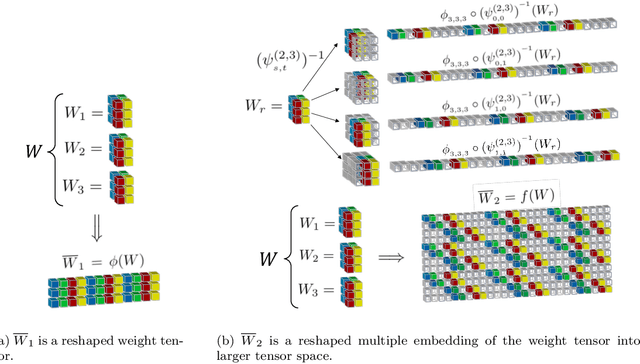
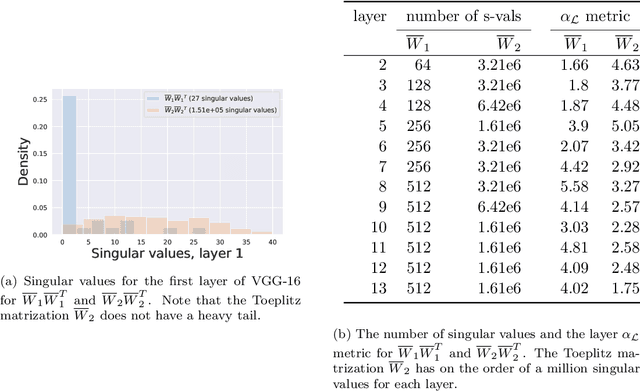
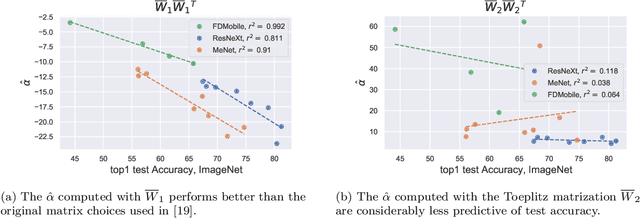
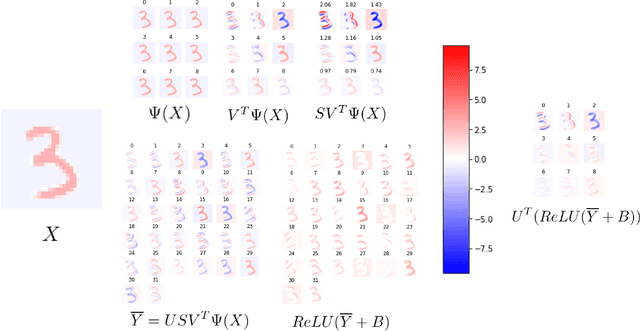
Abstract:Deep neural networks used for image classification often use convolutional filters to extract distinguishing features before passing them to a linear classifier. Most interpretability literature focuses on providing semantic meaning to convolutional filters to explain a model's reasoning process and confirm its use of relevant information from the input domain. Fully connected layers can be studied by decomposing their weight matrices using a singular value decomposition, in effect studying the correlations between the rows in each matrix to discover the dynamics of the map. In this work we define a singular value decomposition for the weight tensor of a convolutional layer, which provides an analogous understanding of the correlations between filters, exposing the dynamics of the convolutional map. We validate our definition using recent results in random matrix theory. By applying the decomposition across the linear layers of an image classification network we suggest a framework against which interpretability methods might be applied using hypergraphs to model class separation. Rather than looking to the activations to explain the network, we use the singular vectors with the greatest corresponding singular values for each linear layer to identify those features most important to the network. We illustrate our approach with examples and introduce the DeepDataProfiler library, the analysis tool used for this study.
Systematic Evaluation of Backdoor Data Poisoning Attacks on Image Classifiers
Apr 24, 2020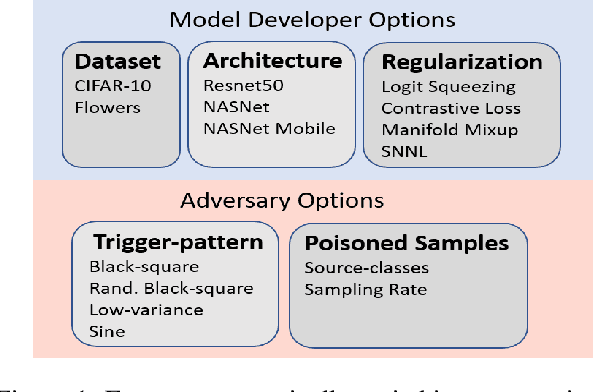


Abstract:Backdoor data poisoning attacks have recently been demonstrated in computer vision research as a potential safety risk for machine learning (ML) systems. Traditional data poisoning attacks manipulate training data to induce unreliability of an ML model, whereas backdoor data poisoning attacks maintain system performance unless the ML model is presented with an input containing an embedded "trigger" that provides a predetermined response advantageous to the adversary. Our work builds upon prior backdoor data-poisoning research for ML image classifiers and systematically assesses different experimental conditions including types of trigger patterns, persistence of trigger patterns during retraining, poisoning strategies, architectures (ResNet-50, NasNet, NasNet-Mobile), datasets (Flowers, CIFAR-10), and potential defensive regularization techniques (Contrastive Loss, Logit Squeezing, Manifold Mixup, Soft-Nearest-Neighbors Loss). Experiments yield four key findings. First, the success rate of backdoor poisoning attacks varies widely, depending on several factors, including model architecture, trigger pattern and regularization technique. Second, we find that poisoned models are hard to detect through performance inspection alone. Third, regularization typically reduces backdoor success rate, although it can have no effect or even slightly increase it, depending on the form of regularization. Finally, backdoors inserted through data poisoning can be rendered ineffective after just a few epochs of additional training on a small set of clean data without affecting the model's performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge