Geometry of the Space of Partitioned Networks: A Unified Theoretical and Computational Framework

Interactions and relations between objects may be pairwise or higher-order in nature, and so network-valued data are ubiquitous in the real world. The "space of networks", however, has a complex structure that cannot be adequately described using conventional statistical tools. We introduce a measure-theoretic formalism for modeling generalized network structures such as graphs, hypergraphs, or graphs whose nodes come with a partition into categorical classes. We then propose a metric that extends the Gromov-Wasserstein distance between graphs and the co-optimal transport distance between hypergraphs. We characterize the geometry of this space, thereby providing a unified theoretical treatment of generalized networks that encompasses the cases of pairwise, as well as higher-order, relations. In particular, we show that our metric is an Alexandrov space of non-negative curvature, and leverage this structure to define gradients for certain functionals commonly arising in geometric data analysis tasks. We extend our analysis to the setting where vertices have additional label information, and derive efficient computational schemes to use in practice. Equipped with these theoretical and computational tools, we demonstrate the utility of our framework in a suite of applications, including hypergraph alignment, clustering and dictionary learning from ensemble data, multi-omics alignment, as well as multiscale network alignment.

Experimental Observations of the Topology of Convolutional Neural Network Activations

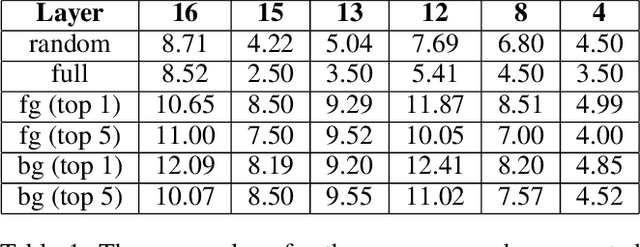
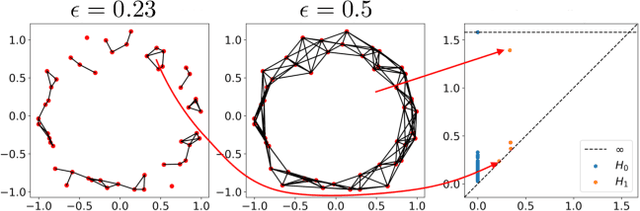
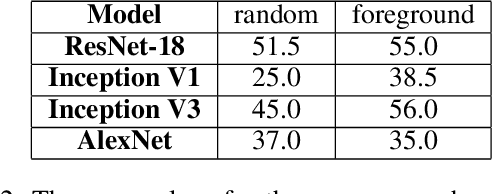
Topological data analysis (TDA) is a branch of computational mathematics, bridging algebraic topology and data science, that provides compact, noise-robust representations of complex structures. Deep neural networks (DNNs) learn millions of parameters associated with a series of transformations defined by the model architecture, resulting in high-dimensional, difficult-to-interpret internal representations of input data. As DNNs become more ubiquitous across multiple sectors of our society, there is increasing recognition that mathematical methods are needed to aid analysts, researchers, and practitioners in understanding and interpreting how these models' internal representations relate to the final classification. In this paper, we apply cutting edge techniques from TDA with the goal of gaining insight into the interpretability of convolutional neural networks used for image classification. We use two common TDA approaches to explore several methods for modeling hidden-layer activations as high-dimensional point clouds, and provide experimental evidence that these point clouds capture valuable structural information about the model's process. First, we demonstrate that a distance metric based on persistent homology can be used to quantify meaningful differences between layers, and we discuss these distances in the broader context of existing representational similarity metrics for neural network interpretability. Second, we show that a mapper graph can provide semantic insight into how these models organize hierarchical class knowledge at each layer. These observations demonstrate that TDA is a useful tool to help deep learning practitioners unlock the hidden structures of their models.

Interpreting Graph Drawing with Multi-Agent Reinforcement Learning

Applying machine learning techniques to graph drawing has become an emergent area of research in visualization. In this paper, we interpret graph drawing as a multi-agent reinforcement learning (MARL) problem. We first demonstrate that a large number of classic graph drawing algorithms, including force-directed layouts and stress majorization, can be interpreted within the framework of MARL. Using this interpretation, a node in the graph is assigned to an agent with a reward function. Via multi-agent reward maximization, we obtain an aesthetically pleasing graph layout that is comparable to the outputs of classic algorithms. The main strength of a MARL framework for graph drawing is that it not only unifies a number of classic drawing algorithms in a general formulation but also supports the creation of novel graph drawing algorithms by introducing a diverse set of reward functions.