Low-Rank Compression of Language Models via Differentiable Rank Selection

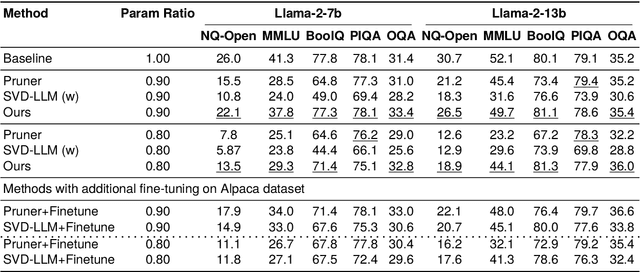
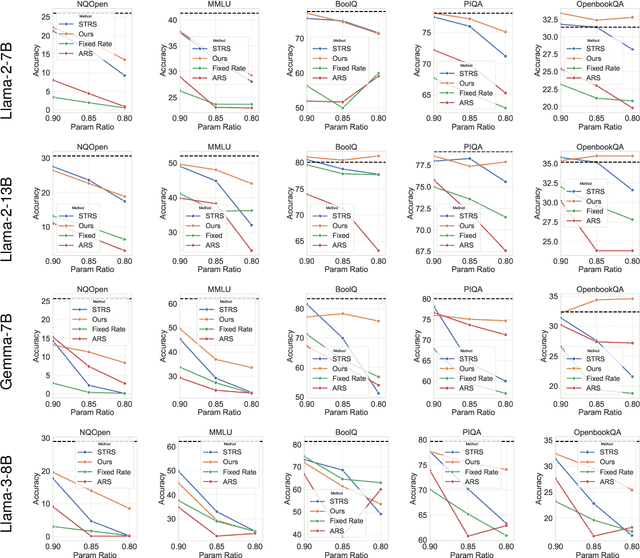
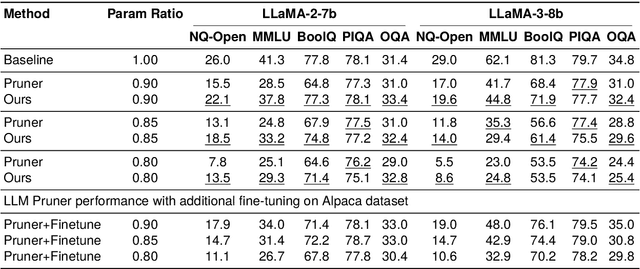
Approaches for compressing large-language models using low-rank decomposition have made strides, particularly with the introduction of activation and loss-aware SVD, which improves the trade-off between decomposition rank and downstream task performance. Despite these advancements, a persistent challenge remains--selecting the optimal ranks for each layer to jointly optimise compression rate and downstream task accuracy. Current methods either rely on heuristics that can yield sub-optimal results due to their limited discrete search space or are gradient-based but are not as performant as heuristic approaches without post-compression fine-tuning. To address these issues, we propose Learning to Low-Rank Compress (LLRC), a gradient-based approach which directly learns the weights of masks that select singular values in a fine-tuning-free setting. Using a calibration dataset, we train only the mask weights to select fewer and fewer singular values while minimising the divergence of intermediate activations from the original model. Our approach outperforms competing ranking selection methods that similarly require no post-compression fine-tuning across various compression rates on common-sense reasoning and open-domain question-answering tasks. For instance, with a compression rate of 20% on Llama-2-13B, LLRC outperforms the competitive Sensitivity-based Truncation Rank Searching (STRS) on MMLU, BoolQ, and OpenbookQA by 12%, 3.5%, and 4.4%, respectively. Compared to other compression techniques, our approach consistently outperforms fine-tuning-free variants of SVD-LLM and LLM-Pruner across datasets and compression rates. Our fine-tuning-free approach also performs competitively with the fine-tuning variant of LLM-Pruner.

Algebraformer: A Neural Approach to Linear Systems

Recent work in deep learning has opened new possibilities for solving classical algorithmic tasks using end-to-end learned models. In this work, we investigate the fundamental task of solving linear systems, particularly those that are ill-conditioned. Existing numerical methods for ill-conditioned systems often require careful parameter tuning, preconditioning, or domain-specific expertise to ensure accuracy and stability. In this work, we propose Algebraformer, a Transformer-based architecture that learns to solve linear systems end-to-end, even in the presence of severe ill-conditioning. Our model leverages a novel encoding scheme that enables efficient representation of matrix and vector inputs, with a memory complexity of $O(n^2)$, supporting scalable inference. We demonstrate its effectiveness on application-driven linear problems, including interpolation tasks from spectral methods for boundary value problems and acceleration of the Newton method. Algebraformer achieves competitive accuracy with significantly lower computational overhead at test time, demonstrating that general-purpose neural architectures can effectively reduce complexity in traditional scientific computing pipelines.

Stuart-Landau Oscillatory Graph Neural Network

Oscillatory Graph Neural Networks (OGNNs) are an emerging class of physics-inspired architectures designed to mitigate oversmoothing and vanishing gradient problems in deep GNNs. In this work, we introduce the Complex-Valued Stuart-Landau Graph Neural Network (SLGNN), a novel architecture grounded in Stuart-Landau oscillator dynamics. Stuart-Landau oscillators are canonical models of limit-cycle behavior near Hopf bifurcations, which are fundamental to synchronization theory and are widely used in e.g. neuroscience for mesoscopic brain modeling. Unlike harmonic oscillators and phase-only Kuramoto models, Stuart-Landau oscillators retain both amplitude and phase dynamics, enabling rich phenomena such as amplitude regulation and multistable synchronization. The proposed SLGNN generalizes existing phase-centric Kuramoto-based OGNNs by allowing node feature amplitudes to evolve dynamically according to Stuart-Landau dynamics, with explicit tunable hyperparameters (such as the Hopf-parameter and the coupling strength) providing additional control over the interplay between feature amplitudes and network structure. We conduct extensive experiments across node classification, graph classification, and graph regression tasks, demonstrating that SLGNN outperforms existing OGNNs and establishes a novel, expressive, and theoretically grounded framework for deep oscillatory architectures on graphs.

Graph-Convolution-Beta-VAE for Synthetic Abdominal Aorta Aneurysm Generation

Synthetic data generation plays a crucial role in medical research by mitigating privacy concerns and enabling large-scale patient data analysis. This study presents a beta-Variational Autoencoder Graph Convolutional Neural Network framework for generating synthetic Abdominal Aorta Aneurysms (AAA). Using a small real-world dataset, our approach extracts key anatomical features and captures complex statistical relationships within a compact disentangled latent space. To address data limitations, low-impact data augmentation based on Procrustes analysis was employed, preserving anatomical integrity. The generation strategies, both deterministic and stochastic, manage to enhance data diversity while ensuring realism. Compared to PCA-based approaches, our model performs more robustly on unseen data by capturing complex, nonlinear anatomical variations. This enables more comprehensive clinical and statistical analyses than the original dataset alone. The resulting synthetic AAA dataset preserves patient privacy while providing a scalable foundation for medical research, device testing, and computational modeling.

Approximation properties of neural ODEs

We study the approximation properties of shallow neural networks whose activation function is defined as the flow of a neural ordinary differential equation (neural ODE) at the final time of the integration interval. We prove the universal approximation property (UAP) of such shallow neural networks in the space of continuous functions. Furthermore, we investigate the approximation properties of shallow neural networks whose parameters are required to satisfy some constraints. In particular, we constrain the Lipschitz constant of the flow of the neural ODE to increase the stability of the shallow neural network, and we restrict the norm of the weight matrices of the linear layers to one to make sure that the restricted expansivity of the flow is not compensated by the increased expansivity of the linear layers. For this setting, we prove approximation bounds that tell us the accuracy to which we can approximate a continuous function with a shallow neural network with such constraints. We prove that the UAP holds if we consider only the constraint on the Lipschitz constant of the flow or the unit norm constraint on the weight matrices of the linear layers.

Efficient Sparsification of Simplicial Complexes via Local Densities of States

Simplicial complexes (SCs), a generalization of graph models for relational data that account for higher-order relations between data items, have become a popular abstraction for analyzing complex data using tools from topological data analysis or topological signal processing. However, the analysis of many real-world datasets leads to dense SCs with a large number of higher-order interactions. Unfortunately, analyzing such large SCs often has a prohibitive cost in terms of computation time and memory consumption. The sparsification of such complexes, i.e., the approximation of an original SC with a sparser simplicial complex with only a log-linear number of high-order simplices while maintaining a spectrum close to the original SC, is of broad interest. In this work, we develop a novel method for a probabilistic sparsifaction of SCs. At its core lies the efficient computation of sparsifying sampling probability through local densities of states as functional descriptors of the spectral information. To avoid pathological structures in the spectrum of the corresponding Hodge Laplacian operators, we suggest a "kernel-ignoring" decomposition for approximating the sampling probability; additionally, we exploit error estimates to show asymptotically prevailing algorithmic complexity of the developed method. The performance of the framework is demonstrated on the family of Vietoris--Rips filtered simplicial complexes.

Rethinking Oversmoothing in Graph Neural Networks: A Rank-Based Perspective

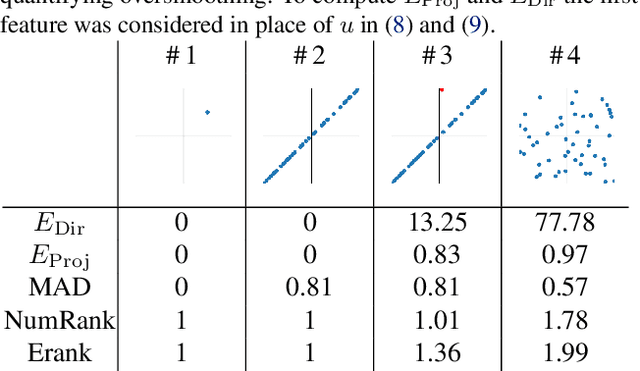
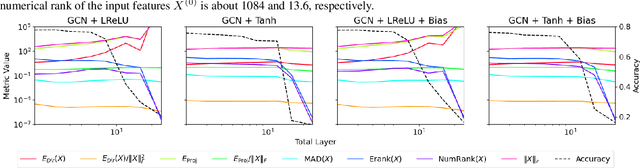
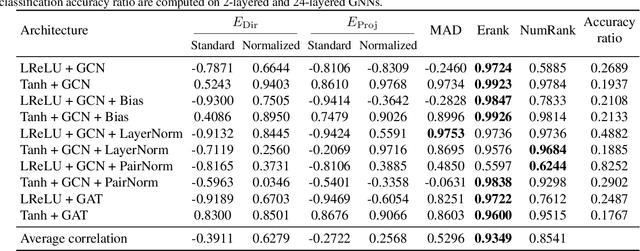
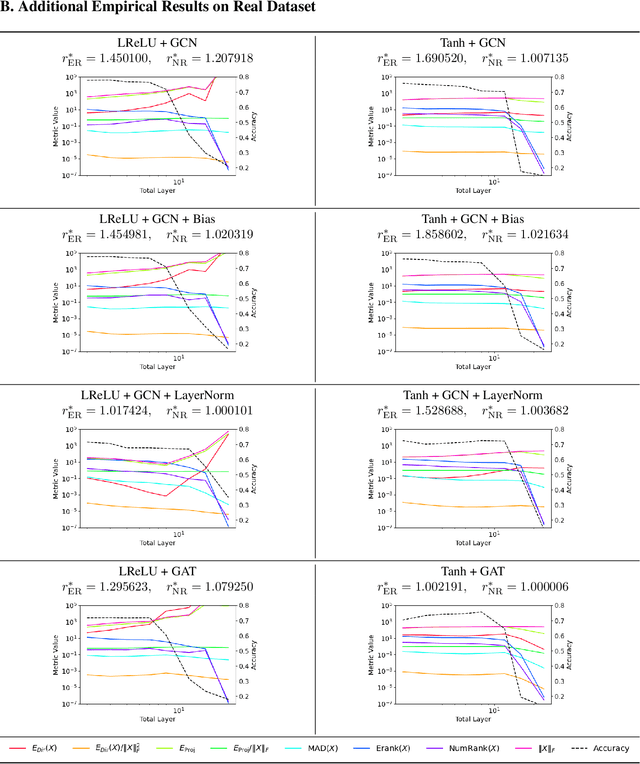
Oversmoothing is a fundamental challenge in graph neural networks (GNNs): as the number of layers increases, node embeddings become increasingly similar, and model performance drops sharply. Traditionally, oversmoothing has been quantified using metrics that measure the similarity of neighbouring node features, such as the Dirichlet energy. While these metrics are related to oversmoothing, we argue they have critical limitations and fail to reliably capture oversmoothing in realistic scenarios. For instance, they provide meaningful insights only for very deep networks and under somewhat strict conditions on the norm of network weights and feature representations. As an alternative, we propose measuring oversmoothing by examining the numerical or effective rank of the feature representations. We provide theoretical support for this approach, demonstrating that the numerical rank of feature representations converges to one for a broad family of nonlinear activation functions under the assumption of nonnegative trained weights. To the best of our knowledge, this is the first result that proves the occurrence of oversmoothing without assumptions on the boundedness of the weight matrices. Along with the theoretical findings, we provide extensive numerical evaluation across diverse graph architectures. Our results show that rank-based metrics consistently capture oversmoothing, whereas energy-based metrics often fail. Notably, we reveal that a significant drop in the rank aligns closely with performance degradation, even in scenarios where energy metrics remain unchanged.

Solaris: A Foundation Model of the Sun

Foundation models have demonstrated remarkable success across various scientific domains, motivating our exploration of their potential in solar physics. In this paper, we present Solaris, the first foundation model for forecasting the Sun's atmosphere. We leverage 13 years of full-disk, multi-wavelength solar imagery from the Solar Dynamics Observatory, spanning a complete solar cycle, to pre-train Solaris for 12-hour interval forecasting. Solaris is built on a large-scale 3D Swin Transformer architecture with 109 million parameters. We demonstrate Solaris' ability to generalize by fine-tuning on a low-data regime using a single wavelength (1700 {\AA}), that was not included in pre-training, outperforming models trained from scratch on this specific wavelength. Our results indicate that Solaris can effectively capture the complex dynamics of the solar atmosphere and transform solar forecasting.

GeoLoRA: Geometric integration for parameter efficient fine-tuning

Low-Rank Adaptation (LoRA) has become a widely used method for parameter-efficient fine-tuning of large-scale, pre-trained neural networks. However, LoRA and its extensions face several challenges, including the need for rank adaptivity, robustness, and computational efficiency during the fine-tuning process. We introduce GeoLoRA, a novel approach that addresses these limitations by leveraging dynamical low-rank approximation theory. GeoLoRA requires only a single backpropagation pass over the small-rank adapters, significantly reducing computational cost as compared to similar dynamical low-rank training methods and making it faster than popular baselines such as AdaLoRA. This allows GeoLoRA to efficiently adapt the allocated parameter budget across the model, achieving smaller low-rank adapters compared to heuristic methods like AdaLoRA and LoRA, while maintaining critical convergence, descent, and error-bound theoretical guarantees. The resulting method is not only more efficient but also more robust to varying hyperparameter settings. We demonstrate the effectiveness of GeoLoRA on several state-of-the-art benchmarks, showing that it outperforms existing methods in both accuracy and computational efficiency.

Low-Rank Adversarial PGD Attack

Adversarial attacks on deep neural network models have seen rapid development and are extensively used to study the stability of these networks. Among various adversarial strategies, Projected Gradient Descent (PGD) is a widely adopted method in computer vision due to its effectiveness and quick implementation, making it suitable for adversarial training. In this work, we observe that in many cases, the perturbations computed using PGD predominantly affect only a portion of the singular value spectrum of the original image, suggesting that these perturbations are approximately low-rank. Motivated by this observation, we propose a variation of PGD that efficiently computes a low-rank attack. We extensively validate our method on a range of standard models as well as robust models that have undergone adversarial training. Our analysis indicates that the proposed low-rank PGD can be effectively used in adversarial training due to its straightforward and fast implementation coupled with competitive performance. Notably, we find that low-rank PGD often performs comparably to, and sometimes even outperforms, the traditional full-rank PGD attack, while using significantly less memory.