Low-Rank Adversarial PGD Attack

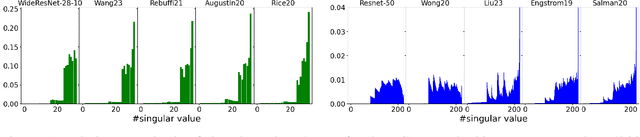
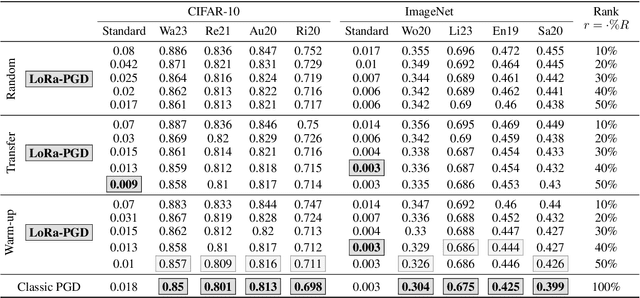
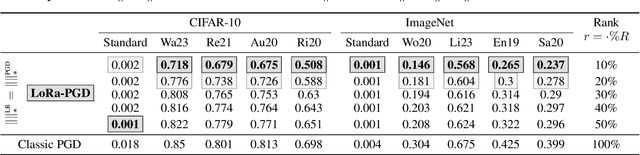
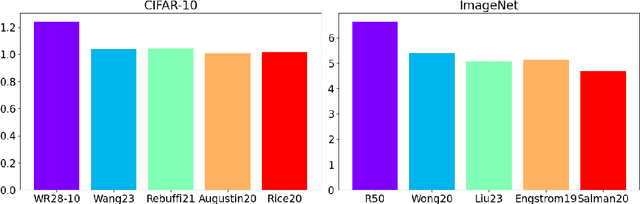
Adversarial attacks on deep neural network models have seen rapid development and are extensively used to study the stability of these networks. Among various adversarial strategies, Projected Gradient Descent (PGD) is a widely adopted method in computer vision due to its effectiveness and quick implementation, making it suitable for adversarial training. In this work, we observe that in many cases, the perturbations computed using PGD predominantly affect only a portion of the singular value spectrum of the original image, suggesting that these perturbations are approximately low-rank. Motivated by this observation, we propose a variation of PGD that efficiently computes a low-rank attack. We extensively validate our method on a range of standard models as well as robust models that have undergone adversarial training. Our analysis indicates that the proposed low-rank PGD can be effectively used in adversarial training due to its straightforward and fast implementation coupled with competitive performance. Notably, we find that low-rank PGD often performs comparably to, and sometimes even outperforms, the traditional full-rank PGD attack, while using significantly less memory.

Robust low-rank training via approximate orthonormal constraints

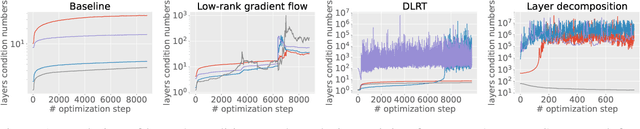
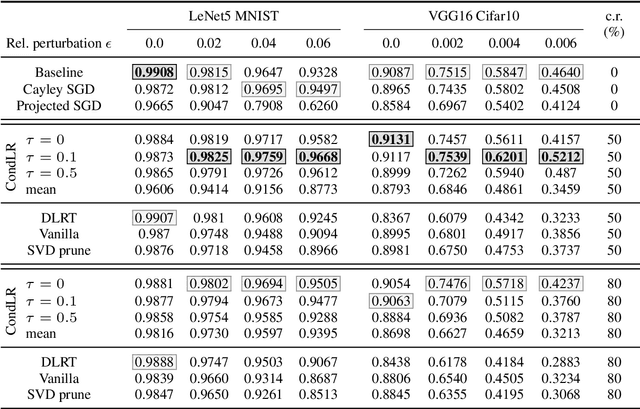
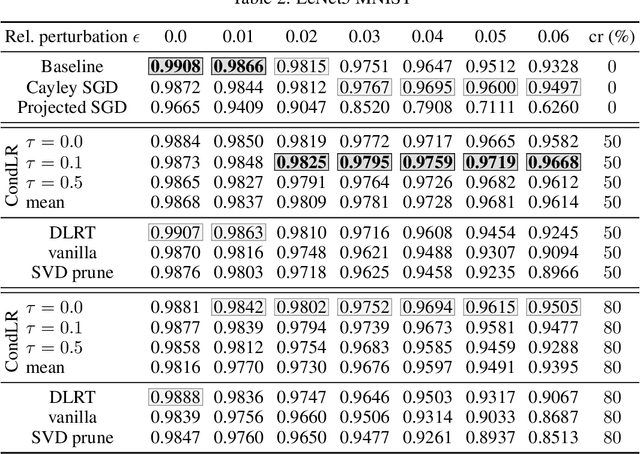
With the growth of model and data sizes, a broad effort has been made to design pruning techniques that reduce the resource demand of deep learning pipelines, while retaining model performance. In order to reduce both inference and training costs, a prominent line of work uses low-rank matrix factorizations to represent the network weights. Although able to retain accuracy, we observe that low-rank methods tend to compromise model robustness against adversarial perturbations. By modeling robustness in terms of the condition number of the neural network, we argue that this loss of robustness is due to the exploding singular values of the low-rank weight matrices. Thus, we introduce a robust low-rank training algorithm that maintains the network's weights on the low-rank matrix manifold while simultaneously enforcing approximate orthonormal constraints. The resulting model reduces both training and inference costs while ensuring well-conditioning and thus better adversarial robustness, without compromising model accuracy. This is shown by extensive numerical evidence and by our main approximation theorem that shows the computed robust low-rank network well-approximates the ideal full model, provided a highly performing low-rank sub-network exists.