GeoLoRA: Geometric integration for parameter efficient fine-tuning

Low-Rank Adaptation (LoRA) has become a widely used method for parameter-efficient fine-tuning of large-scale, pre-trained neural networks. However, LoRA and its extensions face several challenges, including the need for rank adaptivity, robustness, and computational efficiency during the fine-tuning process. We introduce GeoLoRA, a novel approach that addresses these limitations by leveraging dynamical low-rank approximation theory. GeoLoRA requires only a single backpropagation pass over the small-rank adapters, significantly reducing computational cost as compared to similar dynamical low-rank training methods and making it faster than popular baselines such as AdaLoRA. This allows GeoLoRA to efficiently adapt the allocated parameter budget across the model, achieving smaller low-rank adapters compared to heuristic methods like AdaLoRA and LoRA, while maintaining critical convergence, descent, and error-bound theoretical guarantees. The resulting method is not only more efficient but also more robust to varying hyperparameter settings. We demonstrate the effectiveness of GeoLoRA on several state-of-the-art benchmarks, showing that it outperforms existing methods in both accuracy and computational efficiency.

Robust low-rank training via approximate orthonormal constraints

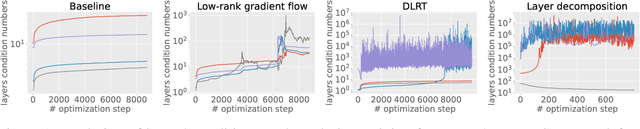
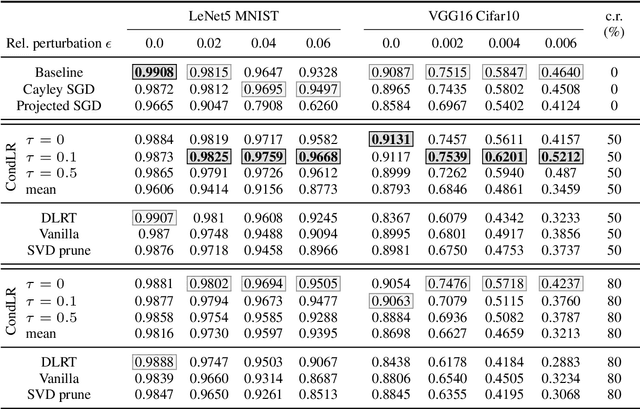
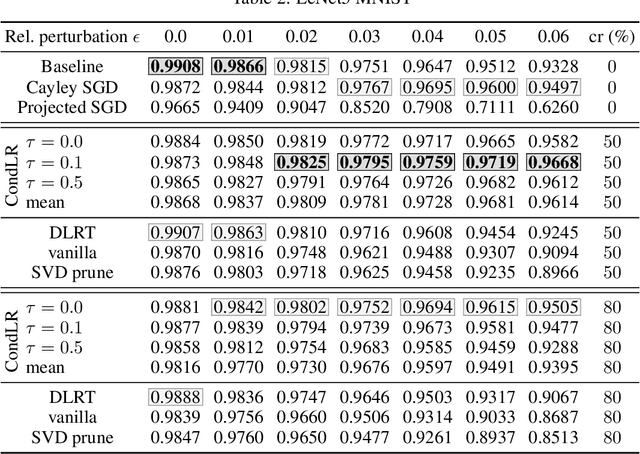
With the growth of model and data sizes, a broad effort has been made to design pruning techniques that reduce the resource demand of deep learning pipelines, while retaining model performance. In order to reduce both inference and training costs, a prominent line of work uses low-rank matrix factorizations to represent the network weights. Although able to retain accuracy, we observe that low-rank methods tend to compromise model robustness against adversarial perturbations. By modeling robustness in terms of the condition number of the neural network, we argue that this loss of robustness is due to the exploding singular values of the low-rank weight matrices. Thus, we introduce a robust low-rank training algorithm that maintains the network's weights on the low-rank matrix manifold while simultaneously enforcing approximate orthonormal constraints. The resulting model reduces both training and inference costs while ensuring well-conditioning and thus better adversarial robustness, without compromising model accuracy. This is shown by extensive numerical evidence and by our main approximation theorem that shows the computed robust low-rank network well-approximates the ideal full model, provided a highly performing low-rank sub-network exists.

Rank-adaptive spectral pruning of convolutional layers during training

The computing cost and memory demand of deep learning pipelines have grown fast in recent years and thus a variety of pruning techniques have been developed to reduce model parameters. The majority of these techniques focus on reducing inference costs by pruning the network after a pass of full training. A smaller number of methods address the reduction of training costs, mostly based on compressing the network via low-rank layer factorizations. Despite their efficiency for linear layers, these methods fail to effectively handle convolutional filters. In this work, we propose a low-parametric training method that factorizes the convolutions into tensor Tucker format and adaptively prunes the Tucker ranks of the convolutional kernel during training. Leveraging fundamental results from geometric integration theory of differential equations on tensor manifolds, we obtain a robust training algorithm that provably approximates the full baseline performance and guarantees loss descent. A variety of experiments against the full model and alternative low-rank baselines are implemented, showing that the proposed method drastically reduces the training costs, while achieving high performance, comparable to or better than the full baseline, and consistently outperforms competing low-rank approaches.

Low-rank lottery tickets: finding efficient low-rank neural networks via matrix differential equations

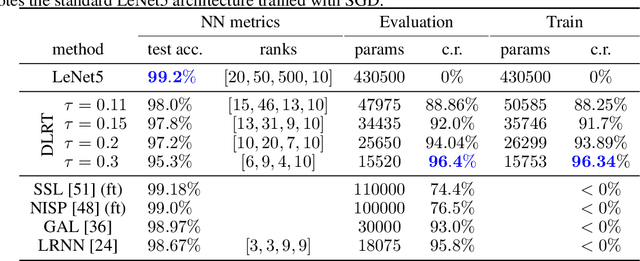
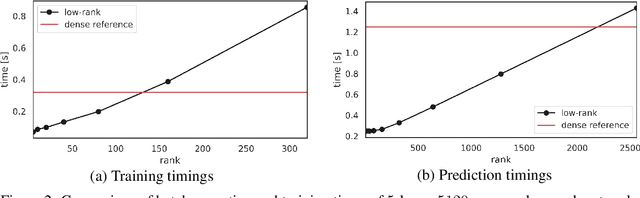
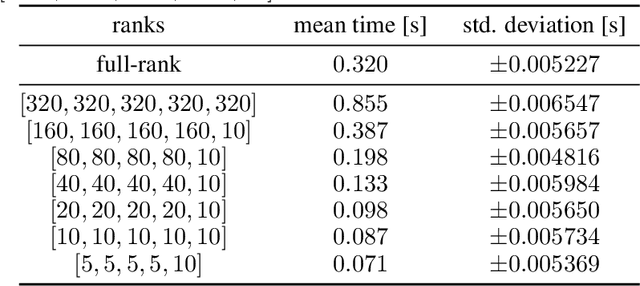
Neural networks have achieved tremendous success in a large variety of applications. However, their memory footprint and computational demand can render them impractical in application settings with limited hardware or energy resources. In this work, we propose a novel algorithm to find efficient low-rank subnetworks. Remarkably, these subnetworks are determined and adapted already during the training phase and the overall time and memory resources required by both training and evaluating them is significantly reduced. The main idea is to restrict the weight matrices to a low-rank manifold and to update the low-rank factors rather than the full matrix during training. To derive training updates that are restricted to the prescribed manifold, we employ techniques from dynamic model order reduction for matrix differential equations. Moreover, our method automatically and dynamically adapts the ranks during training to achieve a desired approximation accuracy. The efficiency of the proposed method is demonstrated through a variety of numerical experiments on fully-connected and convolutional networks.