Local, global and scale-dependent node roles
Paper and Code
May 26, 2021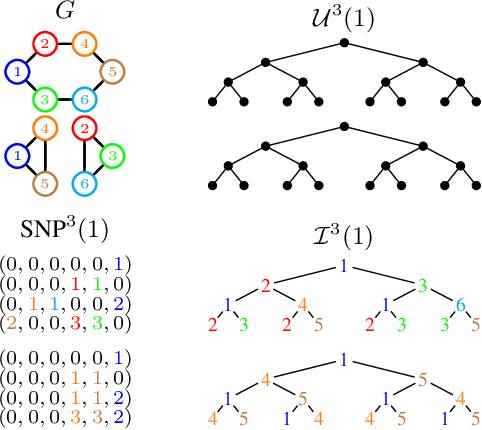
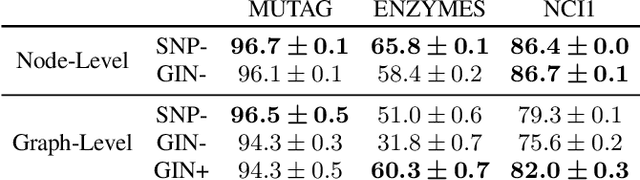
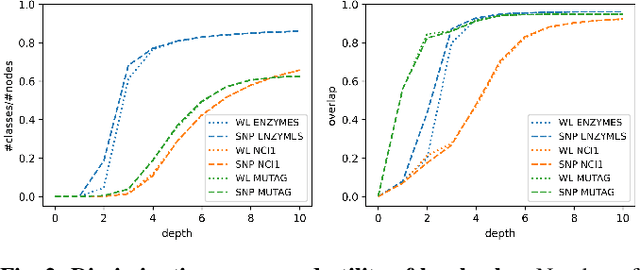
This paper re-examines the concept of node equivalences like structural equivalence or automorphic equivalence, which have originally emerged in social network analysis to characterize the role an actor plays within a social system, but have since then been of independent interest for graph-based learning tasks. Traditionally, such exact node equivalences have been defined either in terms of the one hop neighborhood of a node, or in terms of the global graph structure. Here we formalize exact node roles with a scale-parameter, describing up to what distance the ego network of a node should be considered when assigning node roles - motivated by the idea that there can be local roles of a node that should not be determined by nodes arbitrarily far away in the network. We present numerical experiments that show how already "shallow" roles of depth 3 or 4 carry sufficient information to perform node classification tasks with high accuracy. These findings corroborate the success of recent graph-learning approaches that compute approximate node roles in terms of embeddings, by nonlinearly aggregating node features in an (un)supervised manner over relatively small neighborhood sizes. Indeed, based on our ideas we can construct a shallow classifier achieving on par results with recent graph neural network architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge