Fast Tensor Completion via Approximate Richardson Iteration

We study tensor completion (TC) through the lens of low-rank tensor decomposition (TD). Many TD algorithms use fast alternating minimization methods, which solve highly structured linear regression problems at each step (e.g., for CP, Tucker, and tensor-train decompositions). However, such algebraic structure is lost in TC regression problems, making direct extensions unclear. To address this, we propose a lifting approach that approximately solves TC regression problems using structured TD regression algorithms as blackbox subroutines, enabling sublinear-time methods. We theoretically analyze the convergence rate of our approximate Richardson iteration based algorithm, and we demonstrate on real-world tensors that its running time can be 100x faster than direct methods for CP completion.

GIST: Greedy Independent Set Thresholding for Diverse Data Summarization

We propose a novel subset selection task called min-distance diverse data summarization ($\textsf{MDDS}$), which has a wide variety of applications in machine learning, e.g., data sampling and feature selection. Given a set of points in a metric space, the goal is to maximize an objective that combines the total utility of the points and a diversity term that captures the minimum distance between any pair of selected points, subject to the constraint $|S| \le k$. For example, the points may correspond to training examples in a data sampling problem, e.g., learned embeddings of images extracted from a deep neural network. This work presents the $\texttt{GIST}$ algorithm, which achieves a $\frac{2}{3}$-approximation guarantee for $\textsf{MDDS}$ by approximating a series of maximum independent set problems with a bicriteria greedy algorithm. We also prove a complementary $(\frac{2}{3}+\varepsilon)$-hardness of approximation, for any $\varepsilon > 0$. Finally, we provide an empirical study that demonstrates $\texttt{GIST}$ outperforms existing methods for $\textsf{MDDS}$ on synthetic data, and also for a real-world image classification experiment the studies single-shot subset selection for ImageNet.

PriorBoost: An Adaptive Algorithm for Learning from Aggregate Responses

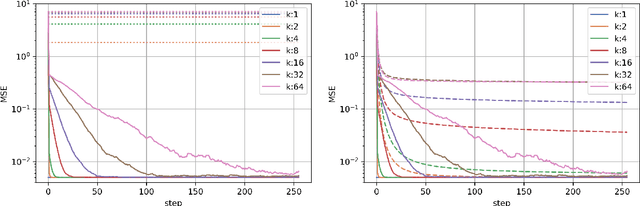
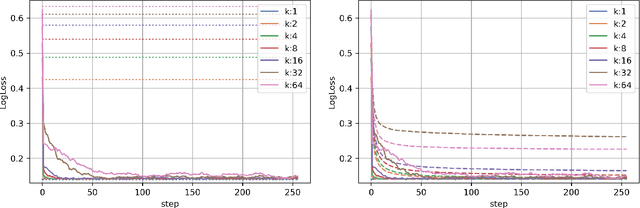
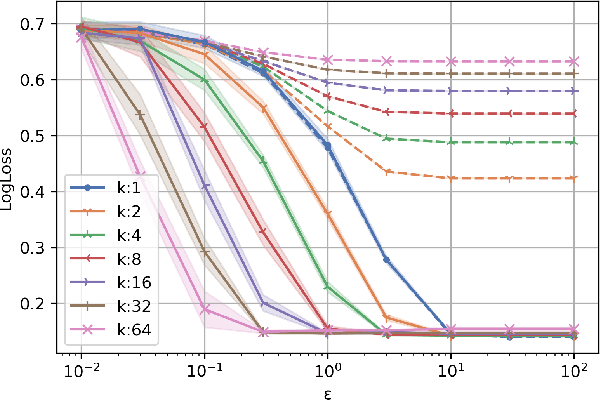
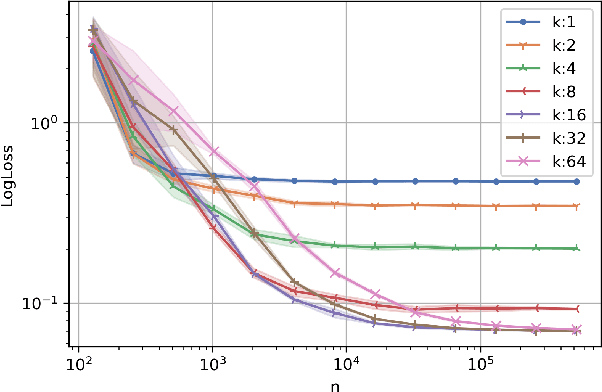
This work studies algorithms for learning from aggregate responses. We focus on the construction of aggregation sets (called bags in the literature) for event-level loss functions. We prove for linear regression and generalized linear models (GLMs) that the optimal bagging problem reduces to one-dimensional size-constrained $k$-means clustering. Further, we theoretically quantify the advantage of using curated bags over random bags. We then propose the PriorBoost algorithm, which adaptively forms bags of samples that are increasingly homogeneous with respect to (unobserved) individual responses to improve model quality. We study label differential privacy for aggregate learning, and we also provide extensive experiments showing that PriorBoost regularly achieves optimal model quality for event-level predictions, in stark contrast to non-adaptive algorithms.

Greedy PIG: Adaptive Integrated Gradients

Deep learning has become the standard approach for most machine learning tasks. While its impact is undeniable, interpreting the predictions of deep learning models from a human perspective remains a challenge. In contrast to model training, model interpretability is harder to quantify and pose as an explicit optimization problem. Inspired by the AUC softmax information curve (AUC SIC) metric for evaluating feature attribution methods, we propose a unified discrete optimization framework for feature attribution and feature selection based on subset selection. This leads to a natural adaptive generalization of the path integrated gradients (PIG) method for feature attribution, which we call Greedy PIG. We demonstrate the success of Greedy PIG on a wide variety of tasks, including image feature attribution, graph compression/explanation, and post-hoc feature selection on tabular data. Our results show that introducing adaptivity is a powerful and versatile method for making attribution methods more powerful.

Pipeline Parallelism for DNN Inference with Practical Performance Guarantees

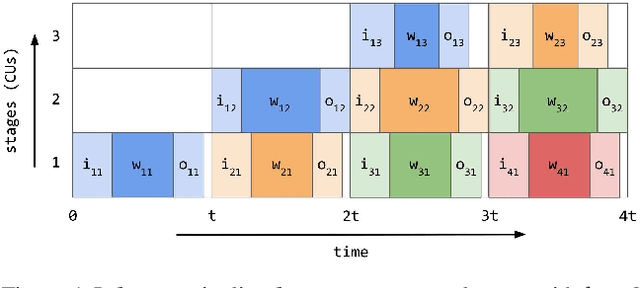
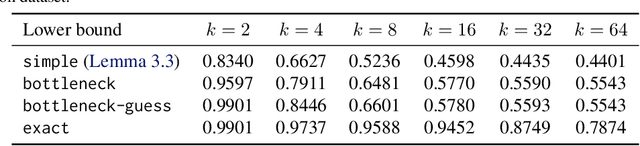
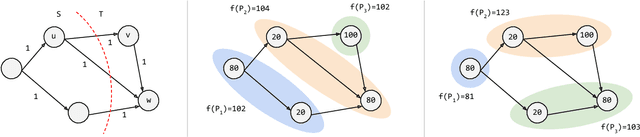
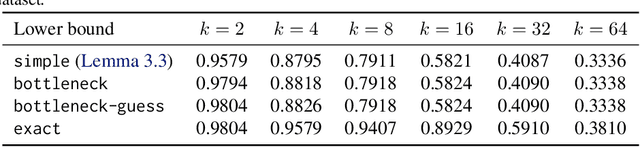
We optimize pipeline parallelism for deep neural network (DNN) inference by partitioning model graphs into $k$ stages and minimizing the running time of the bottleneck stage, including communication. We design practical algorithms for this NP-hard problem and show that they are nearly optimal in practice by comparing against strong lower bounds obtained via novel mixed-integer programming (MIP) formulations. We apply these algorithms and lower-bound methods to production models to achieve substantially improved approximation guarantees compared to standard combinatorial lower bounds. For example, evaluated via geometric means across production data with $k=16$ pipeline stages, our MIP formulations more than double the lower bounds, improving the approximation ratio from $2.175$ to $1.058$. This work shows that while max-throughput partitioning is theoretically hard, we have a handle on the algorithmic side of the problem in practice and much of the remaining challenge is in developing more accurate cost models to feed into the partitioning algorithms.

Unified Embedding: Battle-Tested Feature Representations for Web-Scale ML Systems

Learning high-quality feature embeddings efficiently and effectively is critical for the performance of web-scale machine learning systems. A typical model ingests hundreds of features with vocabularies on the order of millions to billions of tokens. The standard approach is to represent each feature value as a d-dimensional embedding, introducing hundreds of billions of parameters for extremely high-cardinality features. This bottleneck has led to substantial progress in alternative embedding algorithms. Many of these methods, however, make the assumption that each feature uses an independent embedding table. This work introduces a simple yet highly effective framework, Feature Multiplexing, where one single representation space is used across many different categorical features. Our theoretical and empirical analysis reveals that multiplexed embeddings can be decomposed into components from each constituent feature, allowing models to distinguish between features. We show that multiplexed representations lead to Pareto-optimal parameter-accuracy tradeoffs for three public benchmark datasets. Further, we propose a highly practical approach called Unified Embedding with three major benefits: simplified feature configuration, strong adaptation to dynamic data distributions, and compatibility with modern hardware. Unified embedding gives significant improvements in offline and online metrics compared to highly competitive baselines across five web-scale search, ads, and recommender systems, where it serves billions of users across the world in industry-leading products.

Learning Rate Schedules in the Presence of Distribution Shift

We design learning rate schedules that minimize regret for SGD-based online learning in the presence of a changing data distribution. We fully characterize the optimal learning rate schedule for online linear regression via a novel analysis with stochastic differential equations. For general convex loss functions, we propose new learning rate schedules that are robust to distribution shift, and we give upper and lower bounds for the regret that only differ by constants. For non-convex loss functions, we define a notion of regret based on the gradient norm of the estimated models and propose a learning schedule that minimizes an upper bound on the total expected regret. Intuitively, one expects changing loss landscapes to require more exploration, and we confirm that optimal learning rate schedules typically increase in the presence of distribution shift. Finally, we provide experiments for high-dimensional regression models and neural networks to illustrate these learning rate schedules and their cumulative regret.

Approximately Optimal Core Shapes for Tensor Decompositions

This work studies the combinatorial optimization problem of finding an optimal core tensor shape, also called multilinear rank, for a size-constrained Tucker decomposition. We give an algorithm with provable approximation guarantees for its reconstruction error via connections to higher-order singular values. Specifically, we introduce a novel Tucker packing problem, which we prove is NP-hard, and give a polynomial-time approximation scheme based on a reduction to the 2-dimensional knapsack problem with a matroid constraint. We also generalize our techniques to tree tensor network decompositions. We implement our algorithm using an integer programming solver, and show that its solution quality is competitive with (and sometimes better than) the greedy algorithm that uses the true Tucker decomposition loss at each step, while also running up to 1000x faster.

Sequential Attention for Feature Selection

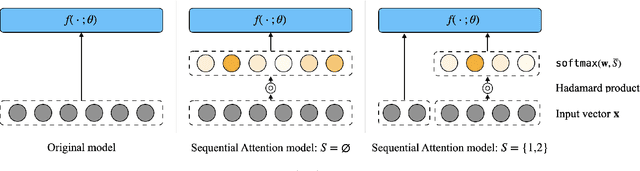
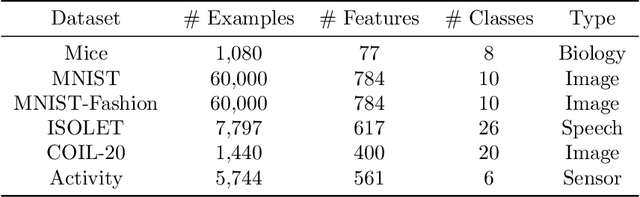
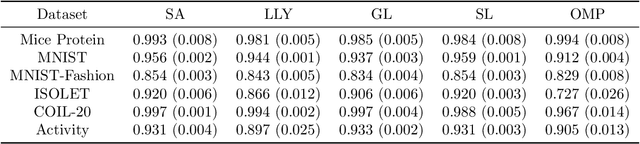
Feature selection is the problem of selecting a subset of features for a machine learning model that maximizes model quality subject to a resource budget constraint. For neural networks, prior methods, including those based on $\ell_1$ regularization, attention, and stochastic gates, typically select all of the features in one evaluation round, ignoring the residual value of the features during selection (i.e., the marginal contribution of a feature conditioned on the previously selected features). We propose a feature selection algorithm called Sequential Attention that achieves state-of-the-art empirical results for neural networks. This algorithm is based on an efficient implementation of greedy forward selection and uses attention weights at each step as a proxy for marginal feature importance. We provide theoretical insights into our Sequential Attention algorithm for linear regression models by showing that an adaptation to this setting is equivalent to the classical Orthogonal Matching Pursuit algorithm [PRK1993], and thus inherits all of its provable guarantees. Lastly, our theoretical and empirical analyses provide new explanations towards the effectiveness of attention and its connections to overparameterization, which might be of independent interest.

Subquadratic Kronecker Regression with Applications to Tensor Decomposition

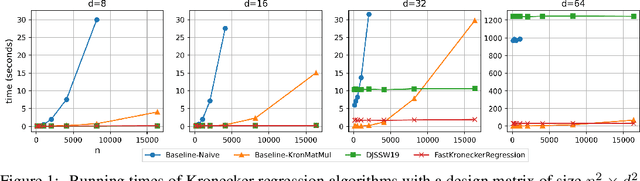
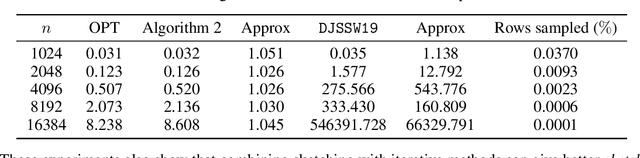
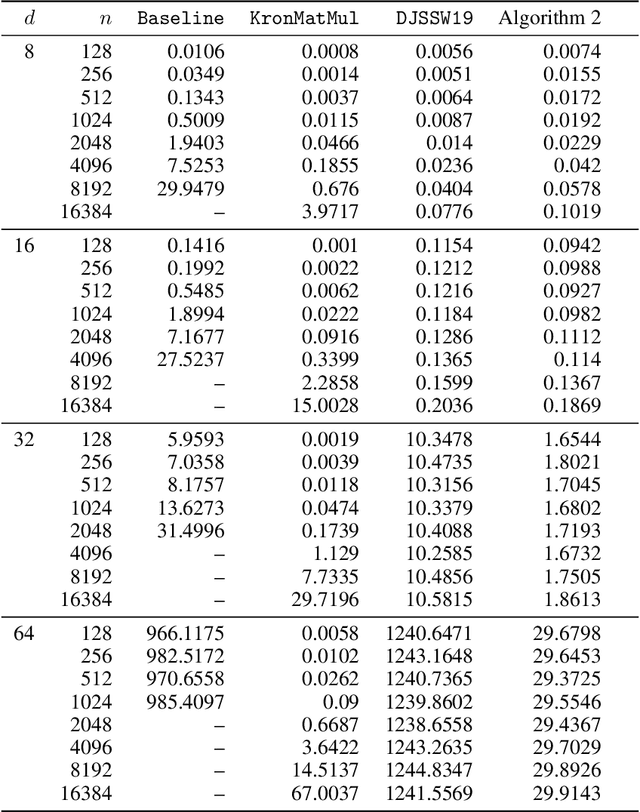
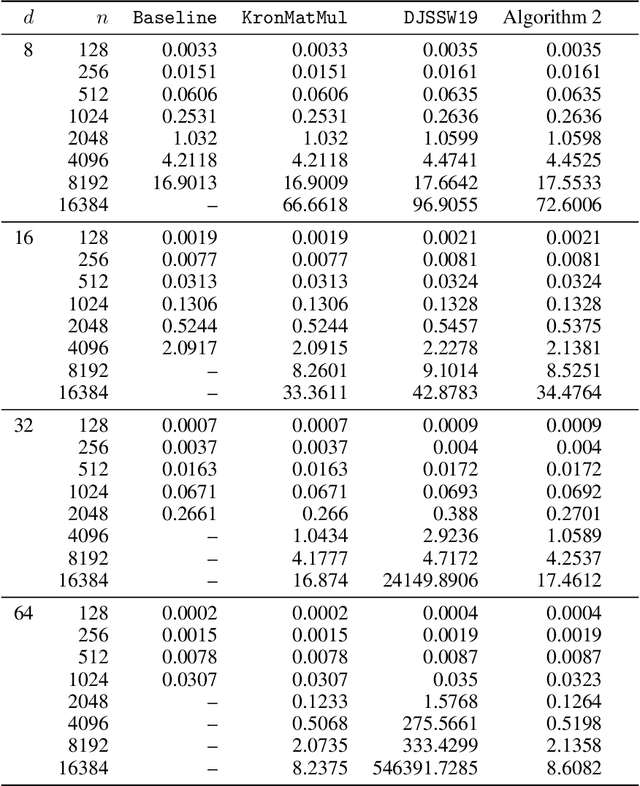
Kronecker regression is a highly-structured least squares problem $\min_{\mathbf{x}} \lVert \mathbf{K}\mathbf{x} - \mathbf{b} \rVert_{2}^2$, where the design matrix $\mathbf{K} = \mathbf{A}^{(1)} \otimes \cdots \otimes \mathbf{A}^{(N)}$ is a Kronecker product of factor matrices. This regression problem arises in each step of the widely-used alternating least squares (ALS) algorithm for computing the Tucker decomposition of a tensor. We present the first subquadratic-time algorithm for solving Kronecker regression to a $(1+\varepsilon)$-approximation that avoids the exponential term $O(\varepsilon^{-N})$ in the running time. Our techniques combine leverage score sampling and iterative methods. By extending our approach to block-design matrices where one block is a Kronecker product, we also achieve subquadratic-time algorithms for (1) Kronecker ridge regression and (2) updating the factor matrix of a Tucker decomposition in ALS, which is not a pure Kronecker regression problem, thereby improving the running time of all steps of Tucker ALS. We demonstrate the speed and accuracy of this Kronecker regression algorithm on synthetic data and real-world image tensors.