SurfR: Surface Reconstruction with Multi-scale Attention

We propose a fast and accurate surface reconstruction algorithm for unorganized point clouds using an implicit representation. Recent learning methods are either single-object representations with small neural models that allow for high surface details but require per-object training or generalized representations that require larger models and generalize to newer shapes but lack details, and inference is slow. We propose a new implicit representation for general 3D shapes that is faster than all the baselines at their optimum resolution, with only a marginal loss in performance compared to the state-of-the-art. We achieve the best accuracy-speed trade-off using three key contributions. Many implicit methods extract features from the point cloud to classify whether a query point is inside or outside the object. First, to speed up the reconstruction, we show that this feature extraction does not need to use the query point at an early stage (lazy query). Second, we use a parallel multi-scale grid representation to develop robust features for different noise levels and input resolutions. Finally, we show that attention across scales can provide improved reconstruction results.

Analyzing Similarity Metrics for Data Selection for Language Model Pretraining

Similarity between training examples is used to curate pretraining datasets for language models by many methods -- for diversification and to select examples similar to high-quality data. However, similarity is typically measured with off-the-shelf embedding models that are generic or trained for tasks such as retrieval. This paper introduces a framework to analyze the suitability of embedding models specifically for data curation in the language model pretraining setting. We quantify the correlation between similarity in the embedding space to similarity in pretraining loss between different training examples, and how diversifying in the embedding space affects pretraining quality. We analyze a variety of embedding models in our framework, with experiments using the Pile dataset for pretraining a 1.7B parameter decoder-only language model. We find that the embedding models we consider are all useful for pretraining data curation. Moreover, a simple approach of averaging per-token embeddings proves to be surprisingly competitive with more sophisticated embedding models -- likely because the latter are not designed specifically for pretraining data curation. Indeed, we believe our analysis and evaluation framework can serve as a foundation for the design of embedding models that specifically reason about similarity in pretraining datasets.

LatentCRF: Continuous CRF for Efficient Latent Diffusion

Latent Diffusion Models (LDMs) produce high-quality, photo-realistic images, however, the latency incurred by multiple costly inference iterations can restrict their applicability. We introduce LatentCRF, a continuous Conditional Random Field (CRF) model, implemented as a neural network layer, that models the spatial and semantic relationships among the latent vectors in the LDM. By replacing some of the computationally-intensive LDM inference iterations with our lightweight LatentCRF, we achieve a superior balance between quality, speed and diversity. We increase inference efficiency by 33% with no loss in image quality or diversity compared to the full LDM. LatentCRF is an easy add-on, which does not require modifying the LDM.

GIST: Greedy Independent Set Thresholding for Diverse Data Summarization

We propose a novel subset selection task called min-distance diverse data summarization ($\textsf{MDDS}$), which has a wide variety of applications in machine learning, e.g., data sampling and feature selection. Given a set of points in a metric space, the goal is to maximize an objective that combines the total utility of the points and a diversity term that captures the minimum distance between any pair of selected points, subject to the constraint $|S| \le k$. For example, the points may correspond to training examples in a data sampling problem, e.g., learned embeddings of images extracted from a deep neural network. This work presents the $\texttt{GIST}$ algorithm, which achieves a $\frac{2}{3}$-approximation guarantee for $\textsf{MDDS}$ by approximating a series of maximum independent set problems with a bicriteria greedy algorithm. We also prove a complementary $(\frac{2}{3}+\varepsilon)$-hardness of approximation, for any $\varepsilon > 0$. Finally, we provide an empirical study that demonstrates $\texttt{GIST}$ outperforms existing methods for $\textsf{MDDS}$ on synthetic data, and also for a real-world image classification experiment the studies single-shot subset selection for ImageNet.

On Distributed Larger-Than-Memory Subset Selection With Pairwise Submodular Functions

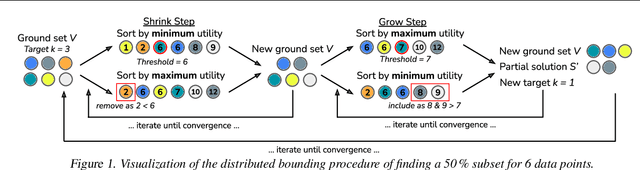
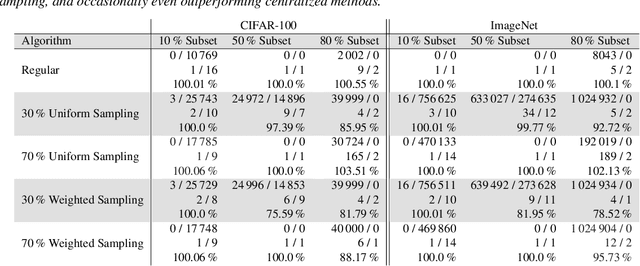
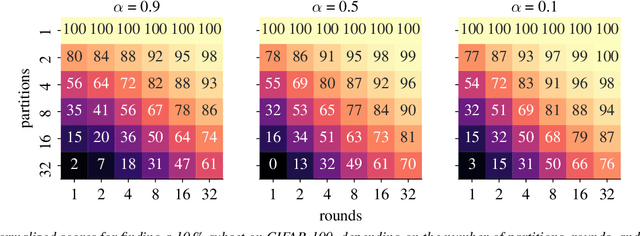
Many learning problems hinge on the fundamental problem of subset selection, i.e., identifying a subset of important and representative points. For example, selecting the most significant samples in ML training cannot only reduce training costs but also enhance model quality. Submodularity, a discrete analogue of convexity, is commonly used for solving subset selection problems. However, existing algorithms for optimizing submodular functions are sequential, and the prior distributed methods require at least one central machine to fit the target subset. In this paper, we relax the requirement of having a central machine for the target subset by proposing a novel distributed bounding algorithm with provable approximation guarantees. The algorithm iteratively bounds the minimum and maximum utility values to select high quality points and discard the unimportant ones. When bounding does not find the complete subset, we use a multi-round, partition-based distributed greedy algorithm to identify the remaining subset. We show that these algorithms find high quality subsets on CIFAR-100 and ImageNet with marginal or no loss in quality compared to centralized methods, and scale to a dataset with 13 billion points.

Simulated Overparameterization

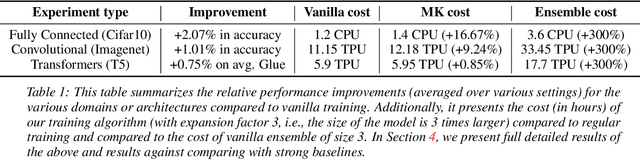
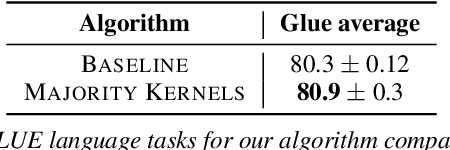
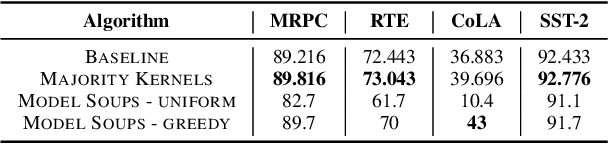
In this work, we introduce a novel paradigm called Simulated Overparametrization (SOP). SOP merges the computational efficiency of compact models with the advanced learning proficiencies of overparameterized models. SOP proposes a unique approach to model training and inference, where a model with a significantly larger number of parameters is trained in such a way that a smaller, efficient subset of these parameters is used for the actual computation during inference. Building upon this framework, we present a novel, architecture agnostic algorithm called "majority kernels", which seamlessly integrates with predominant architectures, including Transformer models. Majority kernels enables the simulated training of overparameterized models, resulting in performance gains across architectures and tasks. Furthermore, our approach adds minimal overhead to the cost incurred (wall clock time) at training time. The proposed approach shows strong performance on a wide variety of datasets and models, even outperforming strong baselines such as combinatorial optimization methods based on submodular optimization.

A Weighted K-Center Algorithm for Data Subset Selection

The success of deep learning hinges on enormous data and large models, which require labor-intensive annotations and heavy computation costs. Subset selection is a fundamental problem that can play a key role in identifying smaller portions of the training data, which can then be used to produce similar models as the ones trained with full data. Two prior methods are shown to achieve impressive results: (1) margin sampling that focuses on selecting points with high uncertainty, and (2) core-sets or clustering methods such as k-center for informative and diverse subsets. We are not aware of any work that combines these methods in a principled manner. To this end, we develop a novel and efficient factor 3-approximation algorithm to compute subsets based on the weighted sum of both k-center and uncertainty sampling objective functions. To handle large datasets, we show a parallel algorithm to run on multiple machines with approximation guarantees. The proposed algorithm achieves similar or better performance compared to other strong baselines on vision datasets such as CIFAR-10, CIFAR-100, and ImageNet.

SPEGTI: Structured Prediction for Efficient Generative Text-to-Image Models

Modern text-to-image generation models produce high-quality images that are both photorealistic and faithful to the text prompts. However, this quality comes at significant computational cost: nearly all of these models are iterative and require running inference multiple times with large models. This iterative process is needed to ensure that different regions of the image are not only aligned with the text prompt, but also compatible with each other. In this work, we propose a light-weight approach to achieving this compatibility between different regions of an image, using a Markov Random Field (MRF) model. This method is shown to work in conjunction with the recently proposed Muse model. The MRF encodes the compatibility among image tokens at different spatial locations and enables us to significantly reduce the required number of Muse prediction steps. Inference with the MRF is significantly cheaper, and its parameters can be quickly learned through back-propagation by modeling MRF inference as a differentiable neural-network layer. Our full model, SPEGTI, uses this proposed MRF model to speed up Muse by 1.5X with no loss in output image quality.

Leveraging Importance Weights in Subset Selection

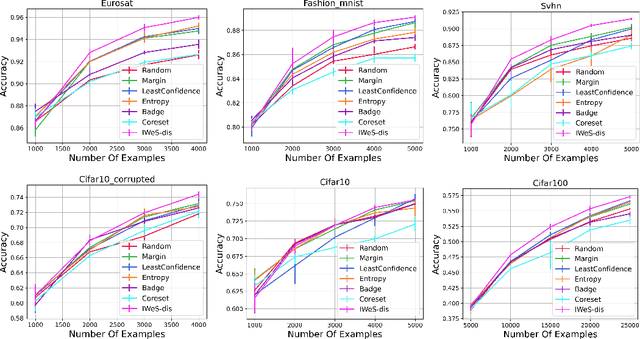
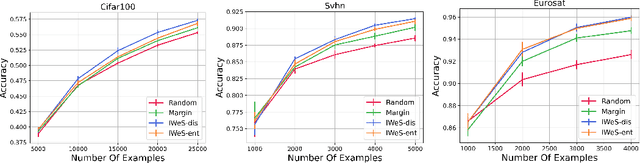
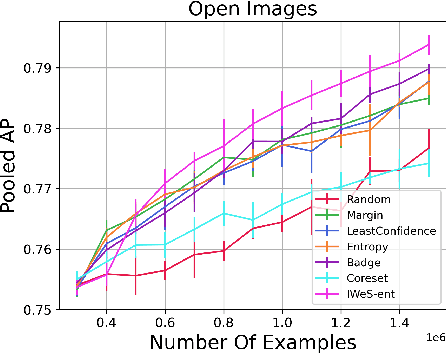
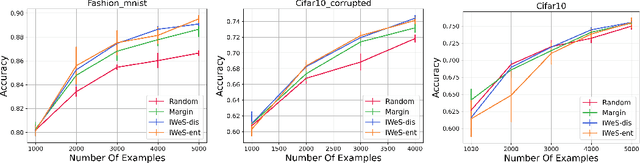
We present a subset selection algorithm designed to work with arbitrary model families in a practical batch setting. In such a setting, an algorithm can sample examples one at a time but, in order to limit overhead costs, is only able to update its state (i.e. further train model weights) once a large enough batch of examples is selected. Our algorithm, IWeS, selects examples by importance sampling where the sampling probability assigned to each example is based on the entropy of models trained on previously selected batches. IWeS admits significant performance improvement compared to other subset selection algorithms for seven publicly available datasets. Additionally, it is competitive in an active learning setting, where the label information is not available at selection time. We also provide an initial theoretical analysis to support our importance weighting approach, proving generalization and sampling rate bounds.

When does mixup promote local linearity in learned representations?

Mixup is a regularization technique that artificially produces new samples using convex combinations of original training points. This simple technique has shown strong empirical performance, and has been heavily used as part of semi-supervised learning techniques such as mixmatch~\citep{berthelot2019mixmatch} and interpolation consistent training (ICT)~\citep{verma2019interpolation}. In this paper, we look at Mixup through a \emph{representation learning} lens in a semi-supervised learning setup. In particular, we study the role of Mixup in promoting linearity in the learned network representations. Towards this, we study two questions: (1) how does the Mixup loss that enforces linearity in the \emph{last} network layer propagate the linearity to the \emph{earlier} layers?; and (2) how does the enforcement of stronger Mixup loss on more than two data points affect the convergence of training? We empirically investigate these properties of Mixup on vision datasets such as CIFAR-10, CIFAR-100 and SVHN. Our results show that supervised Mixup training does not make \emph{all} the network layers linear; in fact the \emph{intermediate layers} become more non-linear during Mixup training compared to a network that is trained \emph{without} Mixup. However, when Mixup is used as an unsupervised loss, we observe that all the network layers become more linear resulting in faster training convergence.