Simulated Overparameterization

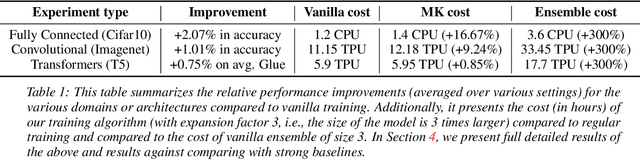
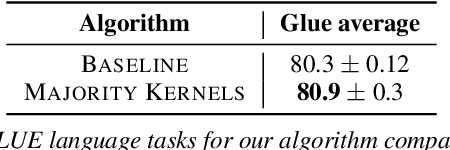
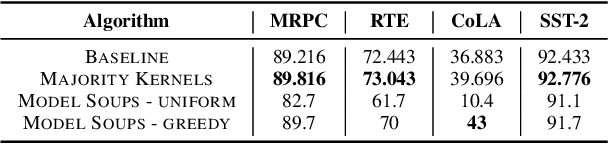
In this work, we introduce a novel paradigm called Simulated Overparametrization (SOP). SOP merges the computational efficiency of compact models with the advanced learning proficiencies of overparameterized models. SOP proposes a unique approach to model training and inference, where a model with a significantly larger number of parameters is trained in such a way that a smaller, efficient subset of these parameters is used for the actual computation during inference. Building upon this framework, we present a novel, architecture agnostic algorithm called "majority kernels", which seamlessly integrates with predominant architectures, including Transformer models. Majority kernels enables the simulated training of overparameterized models, resulting in performance gains across architectures and tasks. Furthermore, our approach adds minimal overhead to the cost incurred (wall clock time) at training time. The proposed approach shows strong performance on a wide variety of datasets and models, even outperforming strong baselines such as combinatorial optimization methods based on submodular optimization.

Deep Fusion: Efficient Network Training via Pre-trained Initializations

In recent years, deep learning has made remarkable progress in a wide range of domains, with a particularly notable impact on natural language processing tasks. One of the challenges associated with training deep neural networks is the need for large amounts of computational resources and time. In this paper, we present Deep Fusion, an efficient approach to network training that leverages pre-trained initializations of smaller networks. % We show that Deep Fusion accelerates the training process, reduces computational requirements, and leads to improved generalization performance on a variety of NLP tasks and T5 model sizes. % Our experiments demonstrate that Deep Fusion is a practical and effective approach to reduce the training time and resource consumption while maintaining, or even surpassing, the performance of traditional training methods.

Towards Task and Architecture-Independent Generalization Gap Predictors

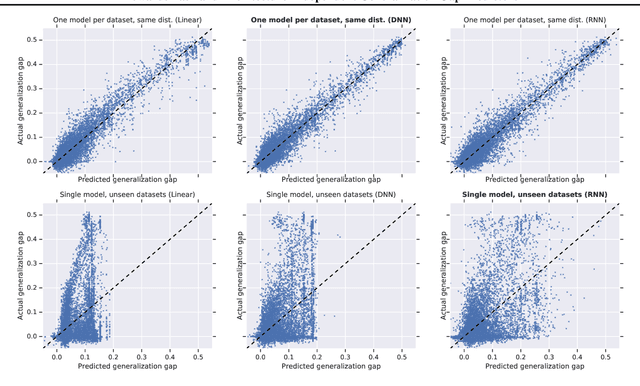
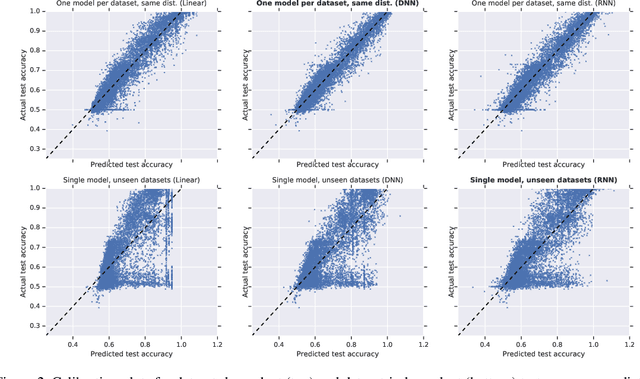
Can we use deep learning to predict when deep learning works? Our results suggest the affirmative. We created a dataset by training 13,500 neural networks with different architectures, on different variations of spiral datasets, and using different optimization parameters. We used this dataset to train task-independent and architecture-independent generalization gap predictors for those neural networks. We extend Jiang et al. (2018) to also use DNNs and RNNs and show that they outperform the linear model, obtaining $R^2=0.965$. We also show results for architecture-independent, task-independent, and out-of-distribution generalization gap prediction tasks. Both DNNs and RNNs consistently and significantly outperform linear models, with RNNs obtaining $R^2=0.584$.

AdaNet: A Scalable and Flexible Framework for Automatically Learning Ensembles

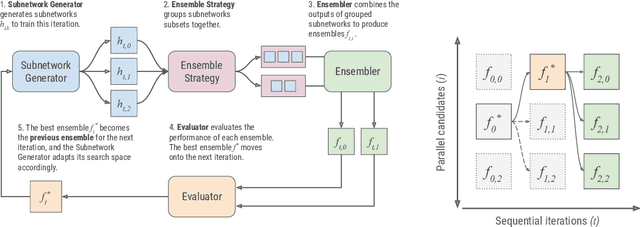
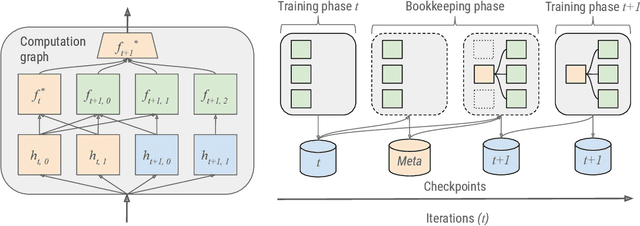
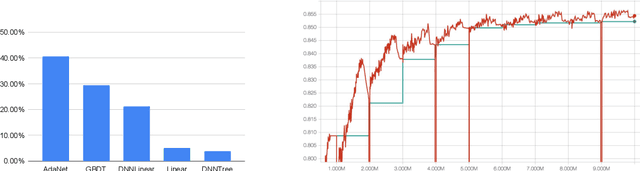
AdaNet is a lightweight TensorFlow-based (Abadi et al., 2015) framework for automatically learning high-quality ensembles with minimal expert intervention. Our framework is inspired by the AdaNet algorithm (Cortes et al., 2017) which learns the structure of a neural network as an ensemble of subnetworks. We designed it to: (1) integrate with the existing TensorFlow ecosystem, (2) offer sensible default search spaces to perform well on novel datasets, (3) present a flexible API to utilize expert information when available, and (4) efficiently accelerate training with distributed CPU, GPU, and TPU hardware. The code is open-source and available at: https://github.com/tensorflow/adanet.

Improving Neural Architecture Search Image Classifiers via Ensemble Learning

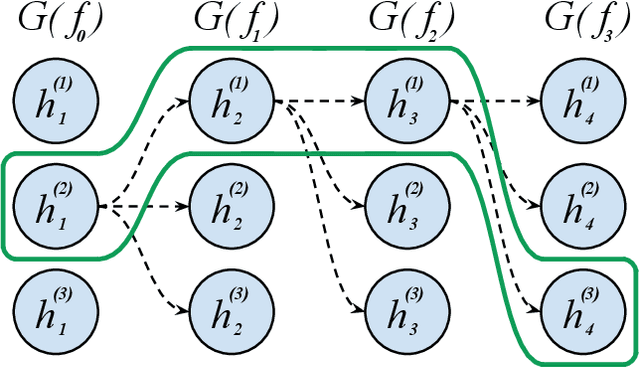
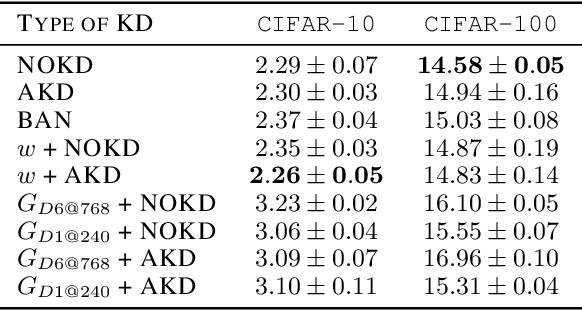
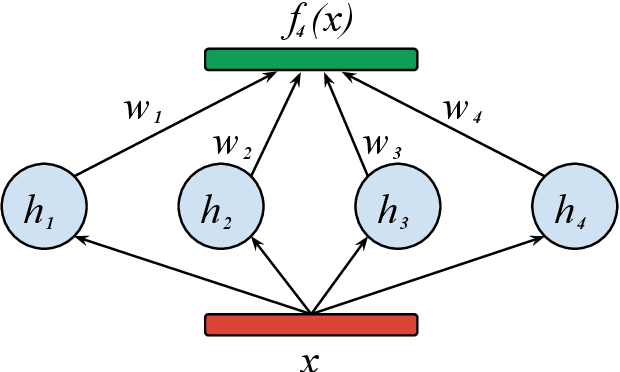
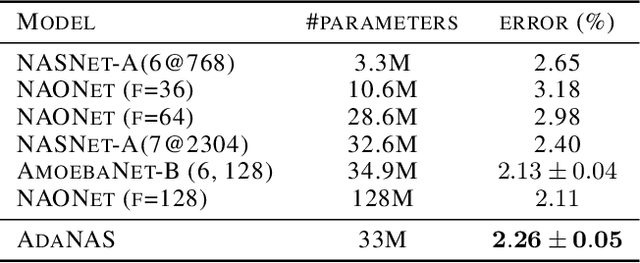
Finding the best neural network architecture requires significant time, resources, and human expertise. These challenges are partially addressed by neural architecture search (NAS) which is able to find the best convolutional layer or cell that is then used as a building block for the network. However, once a good building block is found, manual design is still required to assemble the final architecture as a combination of multiple blocks under a predefined parameter budget constraint. A common solution is to stack these blocks into a single tower and adjust the width and depth to fill the parameter budget. However, these single tower architectures may not be optimal. Instead, in this paper we present the AdaNAS algorithm, that uses ensemble techniques to compose a neural network as an ensemble of smaller networks automatically. Additionally, we introduce a novel technique based on knowledge distillation to iteratively train the smaller networks using the previous ensemble as a teacher. Our experiments demonstrate that ensembles of networks improve accuracy upon a single neural network while keeping the same number of parameters. Our models achieve comparable results with the state-of-the-art on CIFAR-10 and sets a new state-of-the-art on CIFAR-100.

Non-Adaptive Learning a Hidden Hipergraph

We give a new deterministic algorithm that non-adaptively learns a hidden hypergraph from edge-detecting queries. All previous non-adaptive algorithms either run in exponential time or have non-optimal query complexity. We give the first polynomial time non-adaptive learning algorithm for learning hypergraph that asks almost optimal number of queries.

On Exact Learning Monotone DNF from Membership Queries

In this paper, we study the problem of learning a monotone DNF with at most $s$ terms of size (number of variables in each term) at most $r$ ($s$ term $r$-MDNF) from membership queries. This problem is equivalent to the problem of learning a general hypergraph using hyperedge-detecting queries, a problem motivated by applications arising in chemical reactions and genome sequencing. We first present new lower bounds for this problem and then present deterministic and randomized adaptive algorithms with query complexities that are almost optimal. All the algorithms we present in this paper run in time linear in the query complexity and the number of variables $n$. In addition, all of the algorithms we present in this paper are asymptotically tight for fixed $r$ and/or $s$.

Optimal Query Complexity for Reconstructing Hypergraphs

In this paper we consider the problem of reconstructing a hidden weighted hypergraph of constant rank using additive queries. We prove the following: Let $G$ be a weighted hidden hypergraph of constant rank with n vertices and $m$ hyperedges. For any $m$ there exists a non-adaptive algorithm that finds the edges of the graph and their weights using $$ O(\frac{m\log n}{\log m}) $$ additive queries. This solves the open problem in [S. Choi, J. H. Kim. Optimal Query Complexity Bounds for Finding Graphs. {\em STOC}, 749--758,~2008]. When the weights of the hypergraph are integers that are less than $O(poly(n^d/m))$ where $d$ is the rank of the hypergraph (and therefore for unweighted hypergraphs) there exists a non-adaptive algorithm that finds the edges of the graph and their weights using $$ O(\frac{m\log \frac{n^d}{m}}{\log m}). $$ additive queries. Using the information theoretic bound the above query complexities are tight.