On Exact Learning of $d$-Monotone Functions

In this paper, we study the learnability of the Boolean class of $d$-monotone functions $f:{\cal X}\to\{0,1\}$ from membership and equivalence queries, where $({\cal X},\le)$ is a finite lattice. We show that the class of $d$-monotone functions that are represented in the form $f=F(g_1,g_2,\ldots,g_d)$, where $F$ is any Boolean function $F:\{0,1\}^d\to\{0,1\}$ and $g_1,\ldots,g_d:{\cal X}\to \{0,1\}$ are any monotone functions, is learnable in time $\sigma({\cal X})\cdot (size(f)/d+1)^{d}$ where $\sigma({\cal X})$ is the maximum sum of the number of immediate predecessors in a chain from the largest element to the smallest element in the lattice ${\cal X}$ and $size(f)=size(g_1)+\cdots+size(g_d)$, where $size(g_i)$ is the number of minimal elements in $g_i^{-1}(1)$. For the Boolean function $f:\{0,1\}^n\to\{0,1\}$, the class of $d$-monotone functions that are represented in the form $f=F(g_1,g_2,\ldots,g_d)$, where $F$ is any Boolean function and $g_1,\ldots,g_d$ are any monotone DNF, is learnable in time $O(n^2)\cdot (size(f)/d+1)^{d}$ where $size(f)=size(g_1)+\cdots+size(g_d)$. In particular, this class is learnable in polynomial time when $d$ is constant. Additionally, this class is learnable in polynomial time when $size(g_i)$ is constant for all $i$ and $d=O(\log n)$.

Approximating the Number of Relevant Variables in a Parity Implies Proper Learning

Consider the model where we can access a parity function through random uniform labeled examples in the presence of random classification noise. In this paper, we show that approximating the number of relevant variables in the parity function is as hard as properly learning parities. More specifically, let $\gamma:{\mathbb R}^+\to {\mathbb R}^+$, where $\gamma(x) \ge x$, be any strictly increasing function. In our first result, we show that from any polynomial-time algorithm that returns a $\gamma$-approximation, $D$ (i.e., $\gamma^{-1}(d(f)) \leq D \leq \gamma(d(f))$), of the number of relevant variables~$d(f)$ for any parity $f$, we can, in polynomial time, construct a solution to the long-standing open problem of polynomial-time learning $k(n)$-sparse parities (parities with $k(n)\le n$ relevant variables), where $k(n) = \omega_n(1)$. In our second result, we show that from any $T(n)$-time algorithm that, for any parity $f$, returns a $\gamma$-approximation of the number of relevant variables $d(f)$ of $f$, we can, in polynomial time, construct a $poly(\Gamma(n))T(\Gamma(n)^2)$-time algorithm that properly learns parities, where $\Gamma(x)=\gamma(\gamma(x))$. If $T(\Gamma(n)^2)=\exp({o(n/\log n)})$, this would resolve another long-standing open problem of properly learning parities in the presence of random classification noise in time $\exp({o(n/\log n)})$.

On Detecting Some Defective Items in Group Testing

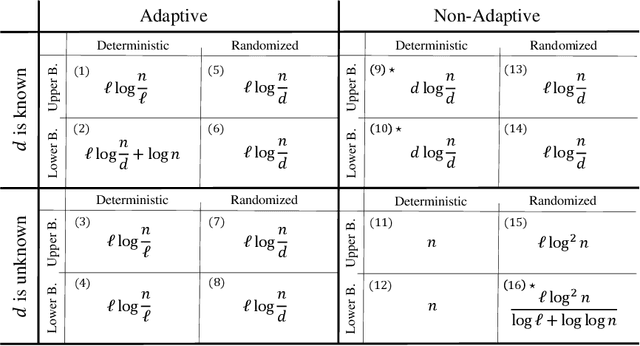
Group testing is an approach aimed at identifying up to $d$ defective items among a total of $n$ elements. This is accomplished by examining subsets to determine if at least one defective item is present. In our study, we focus on the problem of identifying a subset of $\ell\leq d$ defective items. We develop upper and lower bounds on the number of tests required to detect $\ell$ defective items in both the adaptive and non-adaptive settings while considering scenarios where no prior knowledge of $d$ is available, and situations where an estimate of $d$ or at least some non-trivial upper bound on $d$ is available. When no prior knowledge on $d$ is available, we prove a lower bound of $ \Omega(\frac{\ell \log^2n}{\log \ell +\log\log n})$ tests in the randomized non-adaptive settings and an upper bound of $O(\ell \log^2 n)$ for the same settings. Furthermore, we demonstrate that any non-adaptive deterministic algorithm must ask $\Theta(n)$ tests, signifying a fundamental limitation in this scenario. For adaptive algorithms, we establish tight bounds in different scenarios. In the deterministic case, we prove a tight bound of $\Theta(\ell\log{(n/\ell)})$. Moreover, in the randomized settings, we derive a tight bound of $\Theta(\ell\log{(n/d)})$. When $d$, or at least some non-trivial estimate of $d$, is known, we prove a tight bound of $\Theta(d\log (n/d))$ for the deterministic non-adaptive settings, and $\Theta(\ell\log(n/d))$ for the randomized non-adaptive settings. In the adaptive case, we present an upper bound of $O(\ell \log (n/\ell))$ for the deterministic settings, and a lower bound of $\Omega(\ell\log(n/d)+\log n)$. Additionally, we establish a tight bound of $\Theta(\ell \log(n/d))$ for the randomized adaptive settings.

Almost Optimal Proper Learning and Testing Polynomials

We give the first almost optimal polynomial-time proper learning algorithm of Boolean sparse multivariate polynomial under the uniform distribution. For $s$-sparse polynomial over $n$ variables and $\epsilon=1/s^\beta$, $\beta>1$, our algorithm makes $$q_U=\left(\frac{s}{\epsilon}\right)^{\frac{\log \beta}{\beta}+O(\frac{1}{\beta})}+ \tilde O\left(s\right)\left(\log\frac{1}{\epsilon}\right)\log n$$ queries. Notice that our query complexity is sublinear in $1/\epsilon$ and almost linear in $s$. All previous algorithms have query complexity at least quadratic in $s$ and linear in $1/\epsilon$. We then prove the almost tight lower bound $$q_L=\left(\frac{s}{\epsilon}\right)^{\frac{\log \beta}{\beta}+\Omega(\frac{1}{\beta})}+ \Omega\left(s\right)\left(\log\frac{1}{\epsilon}\right)\log n,$$ Applying the reduction in~\cite{Bshouty19b} with the above algorithm, we give the first almost optimal polynomial-time tester for $s$-sparse polynomial. Our tester, for $\beta>3.404$, makes $$\tilde O\left(\frac{s}{\epsilon}\right)$$ queries.

On Learning and Testing Decision Tree

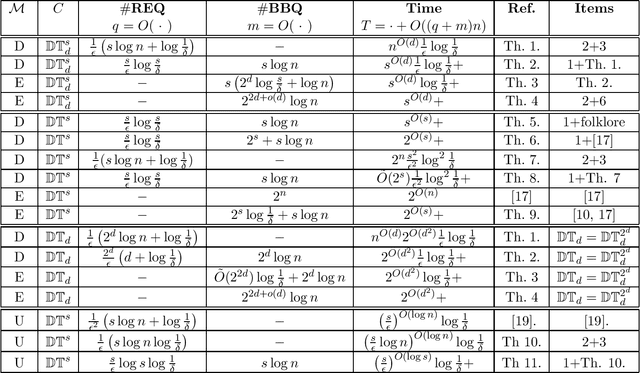
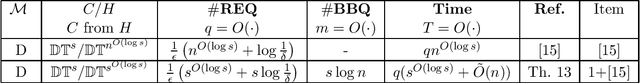
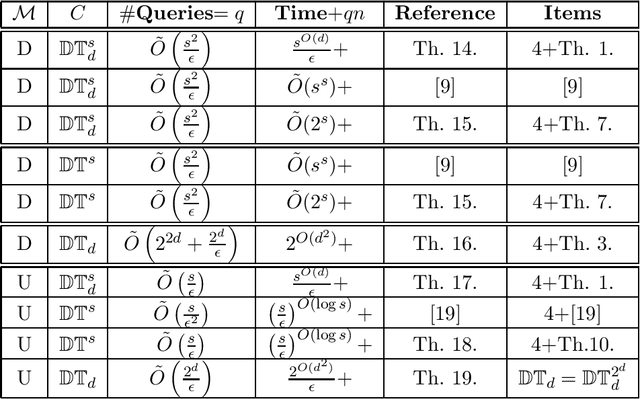
In this paper, we study learning and testing decision tree of size and depth that are significantly smaller than the number of attributes $n$. Our main result addresses the problem of poly$(n,1/\epsilon)$ time algorithms with poly$(s,1/\epsilon)$ query complexity (independent of $n$) that distinguish between functions that are decision trees of size $s$ from functions that are $\epsilon$-far from any decision tree of size $\phi(s,1/\epsilon)$, for some function $\phi > s$. The best known result is the recent one that follows from Blank, Lange and Tan,~\cite{BlancLT20}, that gives $\phi(s,1/\epsilon)=2^{O((\log^3s)/\epsilon^3)}$. In this paper, we give a new algorithm that achieves $\phi(s,1/\epsilon)=2^{O(\log^2 (s/\epsilon))}$. Moreover, we study the testability of depth-$d$ decision tree and give a {\it distribution free} tester that distinguishes between depth-$d$ decision tree and functions that are $\epsilon$-far from depth-$d^2$ decision tree. In particular, for decision trees of size $s$, the above result holds in the distribution-free model when the tree depth is $O(\log(s/\epsilon))$. We also give other new results in learning and testing of size-$s$ decision trees and depth-$d$ decision trees that follow from results in the literature and some results we prove in this paper.

Bounds for the Number of Tests in Non-Adaptive Randomized Algorithms for Group Testing

We study the group testing problem with non-adaptive randomized algorithms. Several models have been discussed in the literature to determine how to randomly choose the tests. For a model ${\cal M}$, let $m_{\cal M}(n,d)$ be the minimum number of tests required to detect at most $d$ defectives within $n$ items, with success probability at least $1-\delta$, for some constant $\delta$. In this paper, we study the measures $$c_{\cal M}(d)=\lim_{n\to \infty} \frac{m_{\cal M}(n,d)}{\ln n} \mbox{ and } c_{\cal M}=\lim_{d\to \infty} \frac{c_{\cal M}(d)}{d}.$$ In the literature, the analyses of such models only give upper bounds for $c_{\cal M}(d)$ and $c_{\cal M}$, and for some of them, the bounds are not tight. We give new analyses that yield tight bounds for $c_{\cal M}(d)$ and $c_{\cal M}$ for all the known models~${\cal M}$.

Adaptive Exact Learning of Decision Trees from Membership Queries

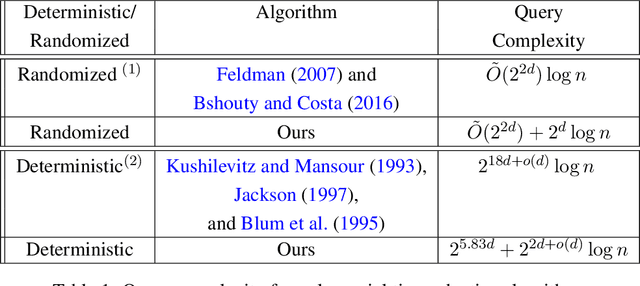
In this paper we study the adaptive learnability of decision trees of depth at most $d$ from membership queries. This has many applications in automated scientific discovery such as drugs development and software update problem. Feldman solves the problem in a randomized polynomial time algorithm that asks $\tilde O(2^{2d})\log n$ queries and Kushilevitz-Mansour in a deterministic polynomial time algorithm that asks $ 2^{18d+o(d)}\log n$ queries. We improve the query complexity of both algorithms. We give a randomized polynomial time algorithm that asks $\tilde O(2^{2d}) + 2^{d}\log n$ queries and a deterministic polynomial time algorithm that asks $2^{5.83d}+2^{2d+o(d)}\log n$ queries.

On Learning Graphs with Edge-Detecting Queries

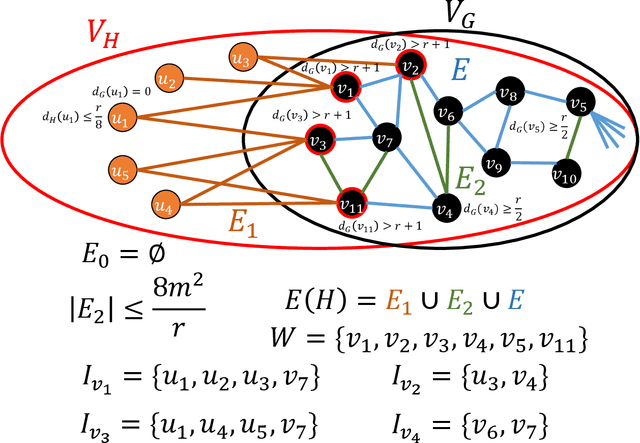
We consider the problem of learning a general graph $G=(V,E)$ using edge-detecting queries, where the number of vertices $|V|=n$ is given to the learner. The information theoretic lower bound gives $m\log n$ for the number of queries, where $m=|E|$ is the number of edges. In case the number of edges $m$ is also given to the learner, Angluin-Chen's Las Vegas algorithm \cite{AC08} runs in $4$ rounds and detects the edges in $O(m\log n)$ queries. In the other harder case where the number of edges $m$ is unknown, their algorithm runs in $5$ rounds and asks $O(m\log n+\sqrt{m}\log^2 n)$ queries. There have been two open problems: \emph{(i)} can the number of queries be reduced to $O(m\log n)$ in the second case, and, \emph{(ii)} can the number of rounds be reduced without substantially increasing the number of queries (in both cases). For the first open problem (when $m$ is unknown) we give two algorithms. The first is an $O(1)$-round Las Vegas algorithm that asks $m\log n+\sqrt{m}(\log^{[k]}n)\log n$ queries for any constant $k$ where $\log^{[k]}n=\log \stackrel{k}{\cdots} \log n$. The second is an $O(\log^*n)$-round Las Vegas algorithm that asks $O(m\log n)$ queries. This solves the first open problem for any practical $n$, for example, $n<2^{65536}$. We also show that no deterministic algorithm can solve this problem in a constant number of rounds. To solve the second problem we study the case when $m$ is known. We first show that any non-adaptive Monte Carlo algorithm (one-round) must ask at least $\Omega(m^2\log n)$ queries, and any two-round Las Vegas algorithm must ask at least $m^{4/3-o(1)}\log n$ queries on average. We then give two two-round Monte Carlo algorithms, the first asks $O(m^{4/3}\log n)$ queries for any $n$ and $m$, and the second asks $O(m\log n)$ queries when $n>2^m$. Finally, we give a $3$-round Monte Carlo algorithm that asks $O(m\log n)$ queries for any $n$ and $m$.

On Polynomial time Constructions of Minimum Height Decision Tree

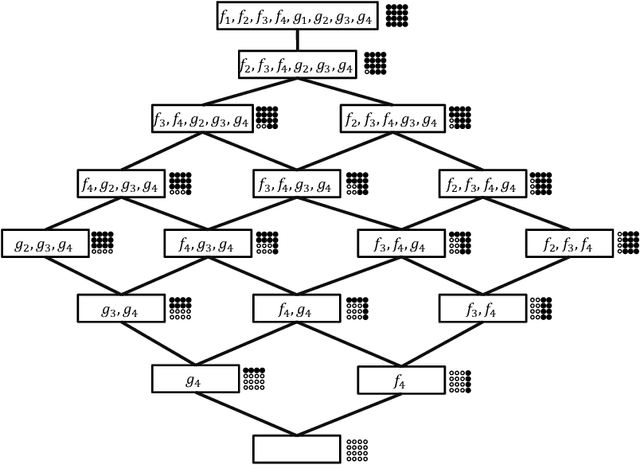
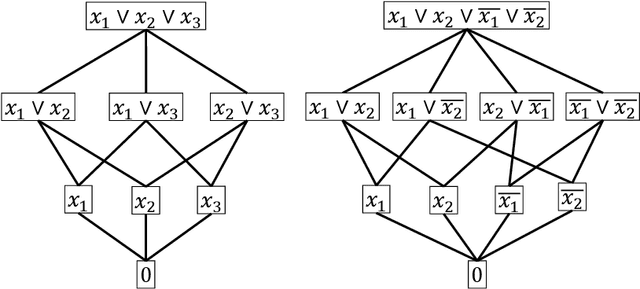
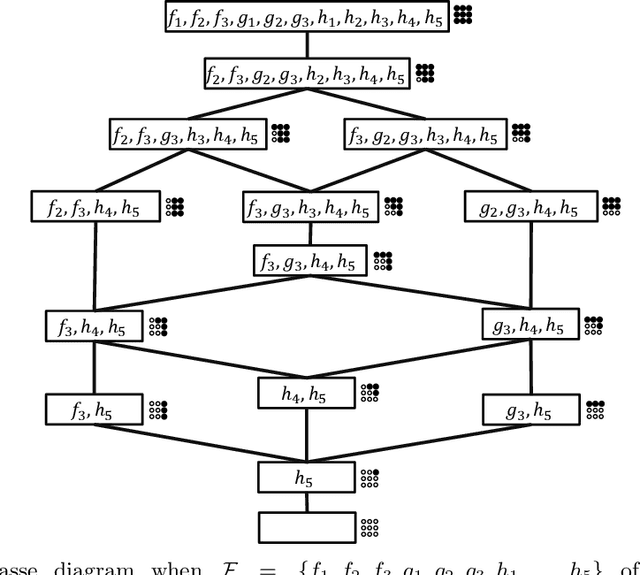
In this paper we study a polynomial time algorithms that for an input $A\subseteq {B_m}$ outputs a decision tree for $A$ of minimum depth. This problem has many applications that include, to name a few, computer vision, group testing, exact learning from membership queries and game theory. Arkin et al. and Moshkov gave a polynomial time $(\ln |A|)$- approximation algorithm (for the depth). The result of Dinur and Steurer for set cover implies that this problem cannot be approximated with ratio $(1-o(1))\cdot \ln |A|$, unless P=NP. Moskov the combinatorial measure of extended teaching dimension of $A$, $ETD(A)$. He showed that $ETD(A)$ is a lower bound for the depth of the decision tree for $A$ and then gave an {\it exponential time} $ETD(A)/\log(ETD(A))$-approximation algorithm. In this paper we further study the $ETD(A)$ measure and a new combinatorial measure, $DEN(A)$, that we call the density of the set $A$. We show that $DEN(A)\le ETD(A)+1$. We then give two results. The first result is that the lower bound $ETD(A)$ of Moshkov for the depth of the decision tree for $A$ is greater than the bounds that are obtained by the classical technique used in the literature. The second result is a polynomial time $(\ln 2) DEN(A)$-approximation (and therefore $(\ln 2) ETD(A)$-approximation) algorithm for the depth of the decision tree of $A$. We also show that a better approximation ratio implies P=NP. We then apply the above results to learning the class of disjunctions of predicates from membership queries. We show that the $ETD$ of this class is bounded from above by the degree $d$ of its Hasse diagram. We then show that Moshkov algorithm can be run in polynomial time and is $(d/\log d)$-approximation algorithm. This gives optimal algorithms when the degree is constant. For example, learning axis parallel rays over constant dimension space.

Non-Adaptive Randomized Algorithm for Group Testing

We study the problem of group testing with a non-adaptive randomized algorithm in the random incidence design (RID) model where each entry in the test is chosen randomly independently from $\{0,1\}$ with a fixed probability $p$. The property that is sufficient and necessary for a unique decoding is the separability of the tests, but unfortunately no linear time algorithm is known for such tests. In order to achieve linear-time decodable tests, the algorithms in the literature use the disjunction property that gives almost optimal number of tests. We define a new property for the tests which we call semi-disjunction property. We show that there is a linear time decoding for such test and for $d\to \infty$ the number of tests converges to the number of tests with the separability property and is therefore optimal (in the RID model). Our analysis shows that, in the RID model, the number of tests in our algorithm is better than the one with the disjunction property even for small $d$.