On Detecting Some Defective Items in Group Testing
Paper and Code
Jun 27, 2023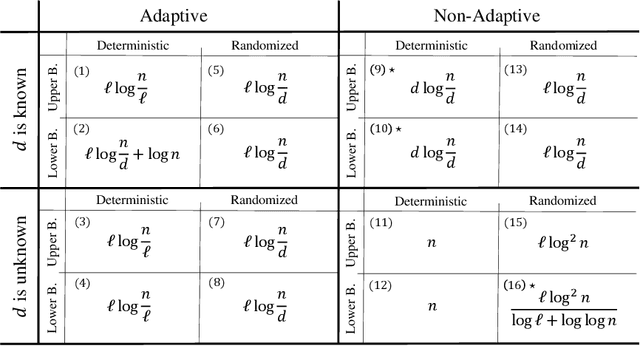

Group testing is an approach aimed at identifying up to $d$ defective items among a total of $n$ elements. This is accomplished by examining subsets to determine if at least one defective item is present. In our study, we focus on the problem of identifying a subset of $\ell\leq d$ defective items. We develop upper and lower bounds on the number of tests required to detect $\ell$ defective items in both the adaptive and non-adaptive settings while considering scenarios where no prior knowledge of $d$ is available, and situations where an estimate of $d$ or at least some non-trivial upper bound on $d$ is available. When no prior knowledge on $d$ is available, we prove a lower bound of $ \Omega(\frac{\ell \log^2n}{\log \ell +\log\log n})$ tests in the randomized non-adaptive settings and an upper bound of $O(\ell \log^2 n)$ for the same settings. Furthermore, we demonstrate that any non-adaptive deterministic algorithm must ask $\Theta(n)$ tests, signifying a fundamental limitation in this scenario. For adaptive algorithms, we establish tight bounds in different scenarios. In the deterministic case, we prove a tight bound of $\Theta(\ell\log{(n/\ell)})$. Moreover, in the randomized settings, we derive a tight bound of $\Theta(\ell\log{(n/d)})$. When $d$, or at least some non-trivial estimate of $d$, is known, we prove a tight bound of $\Theta(d\log (n/d))$ for the deterministic non-adaptive settings, and $\Theta(\ell\log(n/d))$ for the randomized non-adaptive settings. In the adaptive case, we present an upper bound of $O(\ell \log (n/\ell))$ for the deterministic settings, and a lower bound of $\Omega(\ell\log(n/d)+\log n)$. Additionally, we establish a tight bound of $\Theta(\ell \log(n/d))$ for the randomized adaptive settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge