On Detecting Some Defective Items in Group Testing

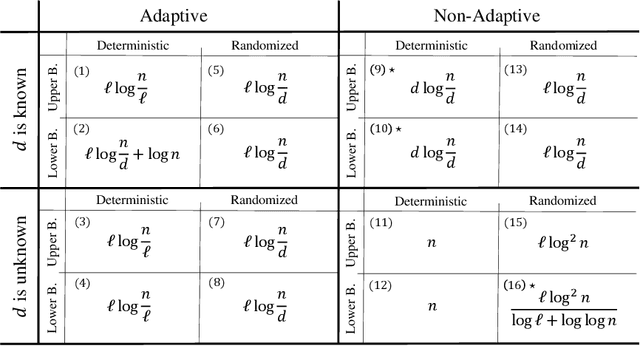
Group testing is an approach aimed at identifying up to $d$ defective items among a total of $n$ elements. This is accomplished by examining subsets to determine if at least one defective item is present. In our study, we focus on the problem of identifying a subset of $\ell\leq d$ defective items. We develop upper and lower bounds on the number of tests required to detect $\ell$ defective items in both the adaptive and non-adaptive settings while considering scenarios where no prior knowledge of $d$ is available, and situations where an estimate of $d$ or at least some non-trivial upper bound on $d$ is available. When no prior knowledge on $d$ is available, we prove a lower bound of $ \Omega(\frac{\ell \log^2n}{\log \ell +\log\log n})$ tests in the randomized non-adaptive settings and an upper bound of $O(\ell \log^2 n)$ for the same settings. Furthermore, we demonstrate that any non-adaptive deterministic algorithm must ask $\Theta(n)$ tests, signifying a fundamental limitation in this scenario. For adaptive algorithms, we establish tight bounds in different scenarios. In the deterministic case, we prove a tight bound of $\Theta(\ell\log{(n/\ell)})$. Moreover, in the randomized settings, we derive a tight bound of $\Theta(\ell\log{(n/d)})$. When $d$, or at least some non-trivial estimate of $d$, is known, we prove a tight bound of $\Theta(d\log (n/d))$ for the deterministic non-adaptive settings, and $\Theta(\ell\log(n/d))$ for the randomized non-adaptive settings. In the adaptive case, we present an upper bound of $O(\ell \log (n/\ell))$ for the deterministic settings, and a lower bound of $\Omega(\ell\log(n/d)+\log n)$. Additionally, we establish a tight bound of $\Theta(\ell \log(n/d))$ for the randomized adaptive settings.

On Learning and Testing Decision Tree

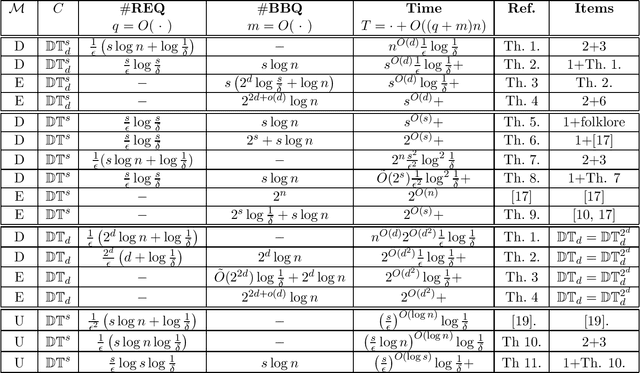
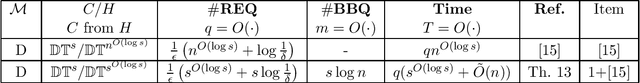
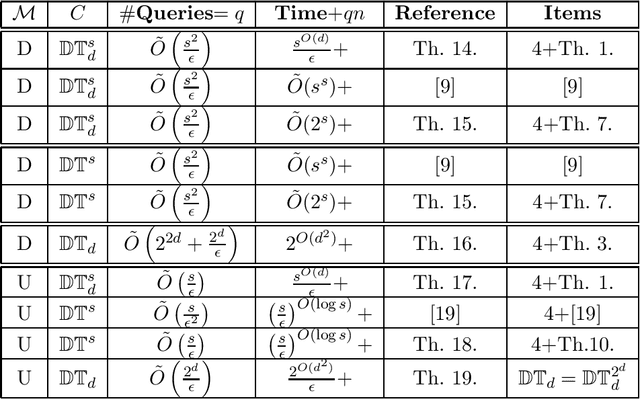
In this paper, we study learning and testing decision tree of size and depth that are significantly smaller than the number of attributes $n$. Our main result addresses the problem of poly$(n,1/\epsilon)$ time algorithms with poly$(s,1/\epsilon)$ query complexity (independent of $n$) that distinguish between functions that are decision trees of size $s$ from functions that are $\epsilon$-far from any decision tree of size $\phi(s,1/\epsilon)$, for some function $\phi > s$. The best known result is the recent one that follows from Blank, Lange and Tan,~\cite{BlancLT20}, that gives $\phi(s,1/\epsilon)=2^{O((\log^3s)/\epsilon^3)}$. In this paper, we give a new algorithm that achieves $\phi(s,1/\epsilon)=2^{O(\log^2 (s/\epsilon))}$. Moreover, we study the testability of depth-$d$ decision tree and give a {\it distribution free} tester that distinguishes between depth-$d$ decision tree and functions that are $\epsilon$-far from depth-$d^2$ decision tree. In particular, for decision trees of size $s$, the above result holds in the distribution-free model when the tree depth is $O(\log(s/\epsilon))$. We also give other new results in learning and testing of size-$s$ decision trees and depth-$d$ decision trees that follow from results in the literature and some results we prove in this paper.

Bounds for the Number of Tests in Non-Adaptive Randomized Algorithms for Group Testing

We study the group testing problem with non-adaptive randomized algorithms. Several models have been discussed in the literature to determine how to randomly choose the tests. For a model ${\cal M}$, let $m_{\cal M}(n,d)$ be the minimum number of tests required to detect at most $d$ defectives within $n$ items, with success probability at least $1-\delta$, for some constant $\delta$. In this paper, we study the measures $$c_{\cal M}(d)=\lim_{n\to \infty} \frac{m_{\cal M}(n,d)}{\ln n} \mbox{ and } c_{\cal M}=\lim_{d\to \infty} \frac{c_{\cal M}(d)}{d}.$$ In the literature, the analyses of such models only give upper bounds for $c_{\cal M}(d)$ and $c_{\cal M}$, and for some of them, the bounds are not tight. We give new analyses that yield tight bounds for $c_{\cal M}(d)$ and $c_{\cal M}$ for all the known models~${\cal M}$.

Adaptive Exact Learning of Decision Trees from Membership Queries

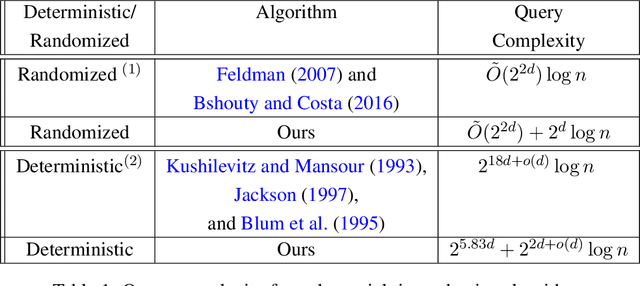
In this paper we study the adaptive learnability of decision trees of depth at most $d$ from membership queries. This has many applications in automated scientific discovery such as drugs development and software update problem. Feldman solves the problem in a randomized polynomial time algorithm that asks $\tilde O(2^{2d})\log n$ queries and Kushilevitz-Mansour in a deterministic polynomial time algorithm that asks $ 2^{18d+o(d)}\log n$ queries. We improve the query complexity of both algorithms. We give a randomized polynomial time algorithm that asks $\tilde O(2^{2d}) + 2^{d}\log n$ queries and a deterministic polynomial time algorithm that asks $2^{5.83d}+2^{2d+o(d)}\log n$ queries.

The Maximum Cosine Framework for Deriving Perceptron Based Linear Classifiers

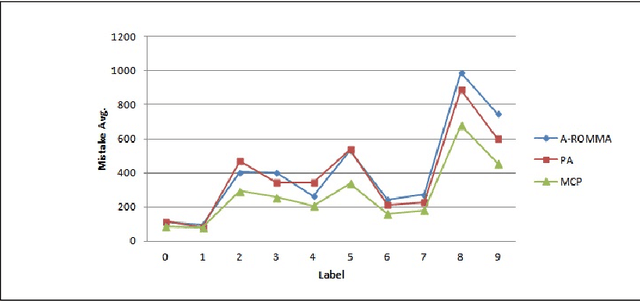
In this work, we introduce a mathematical framework, called the Maximum Cosine Framework or MCF, for deriving new linear classifiers. The method is based on selecting an appropriate bound on the cosine of the angle between the target function and the algorithm's. To justify its correctness, we use the MCF to show how to regenerate the update rule of Aggressive ROMMA. Moreover, we construct a cosine bound from which we build the Maximum Cosine Perceptron algorithm or, for short, the MCP algorithm. We prove that the MCP shares the same mistake bound like the Perceptron. In addition, we demonstrate the promising performance of the MCP on a real dataset. Our experiments show that, under the restriction of single pass learning, the MCP algorithm outperforms PA and Aggressive ROMMA.