On Learning and Testing Decision Tree
Paper and Code
Aug 10, 2021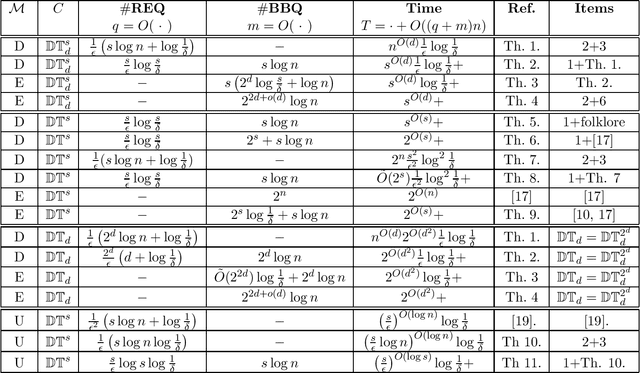
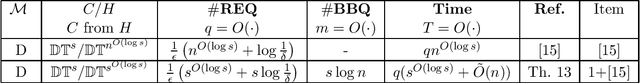
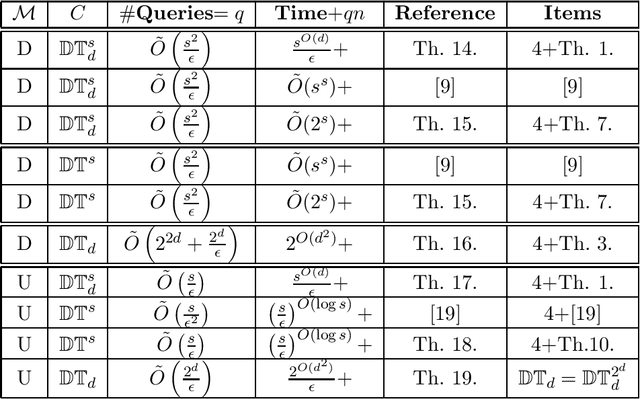

In this paper, we study learning and testing decision tree of size and depth that are significantly smaller than the number of attributes $n$. Our main result addresses the problem of poly$(n,1/\epsilon)$ time algorithms with poly$(s,1/\epsilon)$ query complexity (independent of $n$) that distinguish between functions that are decision trees of size $s$ from functions that are $\epsilon$-far from any decision tree of size $\phi(s,1/\epsilon)$, for some function $\phi > s$. The best known result is the recent one that follows from Blank, Lange and Tan,~\cite{BlancLT20}, that gives $\phi(s,1/\epsilon)=2^{O((\log^3s)/\epsilon^3)}$. In this paper, we give a new algorithm that achieves $\phi(s,1/\epsilon)=2^{O(\log^2 (s/\epsilon))}$. Moreover, we study the testability of depth-$d$ decision tree and give a {\it distribution free} tester that distinguishes between depth-$d$ decision tree and functions that are $\epsilon$-far from depth-$d^2$ decision tree. In particular, for decision trees of size $s$, the above result holds in the distribution-free model when the tree depth is $O(\log(s/\epsilon))$. We also give other new results in learning and testing of size-$s$ decision trees and depth-$d$ decision trees that follow from results in the literature and some results we prove in this paper.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge