On Learning Graphs with Edge-Detecting Queries

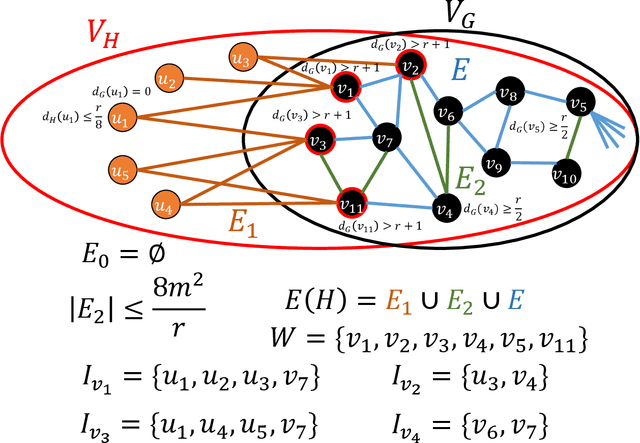
We consider the problem of learning a general graph $G=(V,E)$ using edge-detecting queries, where the number of vertices $|V|=n$ is given to the learner. The information theoretic lower bound gives $m\log n$ for the number of queries, where $m=|E|$ is the number of edges. In case the number of edges $m$ is also given to the learner, Angluin-Chen's Las Vegas algorithm \cite{AC08} runs in $4$ rounds and detects the edges in $O(m\log n)$ queries. In the other harder case where the number of edges $m$ is unknown, their algorithm runs in $5$ rounds and asks $O(m\log n+\sqrt{m}\log^2 n)$ queries. There have been two open problems: \emph{(i)} can the number of queries be reduced to $O(m\log n)$ in the second case, and, \emph{(ii)} can the number of rounds be reduced without substantially increasing the number of queries (in both cases). For the first open problem (when $m$ is unknown) we give two algorithms. The first is an $O(1)$-round Las Vegas algorithm that asks $m\log n+\sqrt{m}(\log^{[k]}n)\log n$ queries for any constant $k$ where $\log^{[k]}n=\log \stackrel{k}{\cdots} \log n$. The second is an $O(\log^*n)$-round Las Vegas algorithm that asks $O(m\log n)$ queries. This solves the first open problem for any practical $n$, for example, $n<2^{65536}$. We also show that no deterministic algorithm can solve this problem in a constant number of rounds. To solve the second problem we study the case when $m$ is known. We first show that any non-adaptive Monte Carlo algorithm (one-round) must ask at least $\Omega(m^2\log n)$ queries, and any two-round Las Vegas algorithm must ask at least $m^{4/3-o(1)}\log n$ queries on average. We then give two two-round Monte Carlo algorithms, the first asks $O(m^{4/3}\log n)$ queries for any $n$ and $m$, and the second asks $O(m\log n)$ queries when $n>2^m$. Finally, we give a $3$-round Monte Carlo algorithm that asks $O(m\log n)$ queries for any $n$ and $m$.

Non-Adaptive Learning a Hidden Hipergraph

We give a new deterministic algorithm that non-adaptively learns a hidden hypergraph from edge-detecting queries. All previous non-adaptive algorithms either run in exponential time or have non-optimal query complexity. We give the first polynomial time non-adaptive learning algorithm for learning hypergraph that asks almost optimal number of queries.

Learning Boolean Halfspaces with Small Weights from Membership Queries

We consider the problem of proper learning a Boolean Halfspace with integer weights $\{0,1,\ldots,t\}$ from membership queries only. The best known algorithm for this problem is an adaptive algorithm that asks $n^{O(t^5)}$ membership queries where the best lower bound for the number of membership queries is $n^t$ [Learning Threshold Functions with Small Weights Using Membership Queries. COLT 1999] In this paper we close this gap and give an adaptive proper learning algorithm with two rounds that asks $n^{O(t)}$ membership queries. We also give a non-adaptive proper learning algorithm that asks $n^{O(t^3)}$ membership queries.

On Exact Learning Monotone DNF from Membership Queries

In this paper, we study the problem of learning a monotone DNF with at most $s$ terms of size (number of variables in each term) at most $r$ ($s$ term $r$-MDNF) from membership queries. This problem is equivalent to the problem of learning a general hypergraph using hyperedge-detecting queries, a problem motivated by applications arising in chemical reactions and genome sequencing. We first present new lower bounds for this problem and then present deterministic and randomized adaptive algorithms with query complexities that are almost optimal. All the algorithms we present in this paper run in time linear in the query complexity and the number of variables $n$. In addition, all of the algorithms we present in this paper are asymptotically tight for fixed $r$ and/or $s$.