On Learning Graphs with Edge-Detecting Queries
Paper and Code
Mar 28, 2018


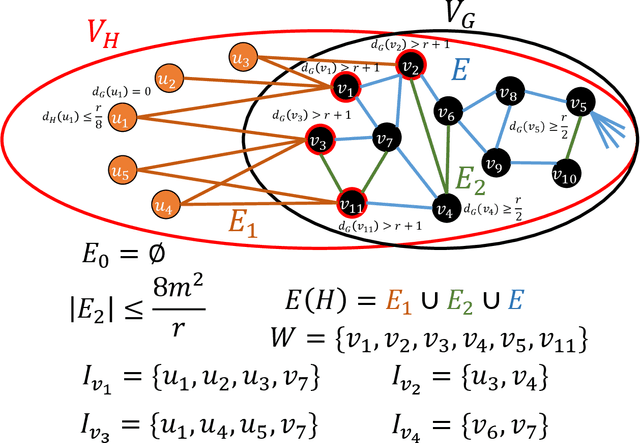
We consider the problem of learning a general graph $G=(V,E)$ using edge-detecting queries, where the number of vertices $|V|=n$ is given to the learner. The information theoretic lower bound gives $m\log n$ for the number of queries, where $m=|E|$ is the number of edges. In case the number of edges $m$ is also given to the learner, Angluin-Chen's Las Vegas algorithm \cite{AC08} runs in $4$ rounds and detects the edges in $O(m\log n)$ queries. In the other harder case where the number of edges $m$ is unknown, their algorithm runs in $5$ rounds and asks $O(m\log n+\sqrt{m}\log^2 n)$ queries. There have been two open problems: \emph{(i)} can the number of queries be reduced to $O(m\log n)$ in the second case, and, \emph{(ii)} can the number of rounds be reduced without substantially increasing the number of queries (in both cases). For the first open problem (when $m$ is unknown) we give two algorithms. The first is an $O(1)$-round Las Vegas algorithm that asks $m\log n+\sqrt{m}(\log^{[k]}n)\log n$ queries for any constant $k$ where $\log^{[k]}n=\log \stackrel{k}{\cdots} \log n$. The second is an $O(\log^*n)$-round Las Vegas algorithm that asks $O(m\log n)$ queries. This solves the first open problem for any practical $n$, for example, $n<2^{65536}$. We also show that no deterministic algorithm can solve this problem in a constant number of rounds. To solve the second problem we study the case when $m$ is known. We first show that any non-adaptive Monte Carlo algorithm (one-round) must ask at least $\Omega(m^2\log n)$ queries, and any two-round Las Vegas algorithm must ask at least $m^{4/3-o(1)}\log n$ queries on average. We then give two two-round Monte Carlo algorithms, the first asks $O(m^{4/3}\log n)$ queries for any $n$ and $m$, and the second asks $O(m\log n)$ queries when $n>2^m$. Finally, we give a $3$-round Monte Carlo algorithm that asks $O(m\log n)$ queries for any $n$ and $m$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge