Training in reverse: How iteration order influences convergence and stability in deep learning

Despite exceptional achievements, training neural networks remains computationally expensive and is often plagued by instabilities that can degrade convergence. While learning rate schedules can help mitigate these issues, finding optimal schedules is time-consuming and resource-intensive. This work explores theoretical issues concerning training stability in the constant-learning-rate (i.e., without schedule) and small-batch-size regime. Surprisingly, we show that the order of gradient updates affects stability and convergence in gradient-based optimizers. We illustrate this new line of thinking using backward-SGD, which processes batch gradient updates like SGD but in reverse order. Our theoretical analysis shows that in contractive regions (e.g., around minima) backward-SGD converges to a point while the standard forward-SGD generally only converges to a distribution. This leads to improved stability and convergence which we demonstrate experimentally. While full backward-SGD is computationally intensive in practice, it highlights opportunities to exploit reverse training dynamics (or more generally alternate iteration orders) to improve training. To our knowledge, this represents a new and unexplored avenue in deep learning optimization.

Sequential inductive prediction intervals

In this paper we explore the concept of sequential inductive prediction intervals using theory from sequential testing. We furthermore introduce a 3-parameter PAC definition of prediction intervals that allows us via simulation to achieve almost sharp bounds with high probability.

Exploring Singularities in point clouds with the graph Laplacian: An explicit approach

We develop theory and methods that use the graph Laplacian to analyze the geometry of the underlying manifold of point clouds. Our theory provides theoretical guarantees and explicit bounds on the functional form of the graph Laplacian, in the case when it acts on functions defined close to singularities of the underlying manifold. We also propose methods that can be used to estimate these geometric properties of the point cloud, which are based on the theoretical guarantees.

Concentration inequalities for leave-one-out cross validation

In this article we prove that estimator stability is enough to show that leave-one-out cross validation is a sound procedure, by providing concentration bounds in a general framework. In particular, we provide concentration bounds beyond Lipschitz continuity assumptions on the loss or on the estimator. In order to obtain our results, we rely on random variables with distribution satisfying the logarithmic Sobolev inequality, providing us a relatively rich class of distributions. We illustrate our method by considering several interesting examples, including linear regression, kernel density estimation, and stabilized / truncated estimators such as stabilized kernel regression.

Deep limits and cut-off phenomena for neural networks

We consider dynamical and geometrical aspects of deep learning. For many standard choices of layer maps we display semi-invariant metrics which quantify differences between data or decision functions. This allows us, when considering random layer maps and using non-commutative ergodic theorems, to deduce that certain limits exist when letting the number of layers tend to infinity. We also examine the random initialization of standard networks where we observe a surprising cut-off phenomenon in terms of the number of layers, the depth of the network. This could be a relevant parameter when choosing an appropriate number of layers for a given learning task, or for selecting a good initialization procedure. More generally, we hope that the notions and results in this paper can provide a framework, in particular a geometric one, for a part of the theoretical understanding of deep neural networks.

Uncertainty-Aware Body Composition Analysis with Deep Regression Ensembles on UK Biobank MRI

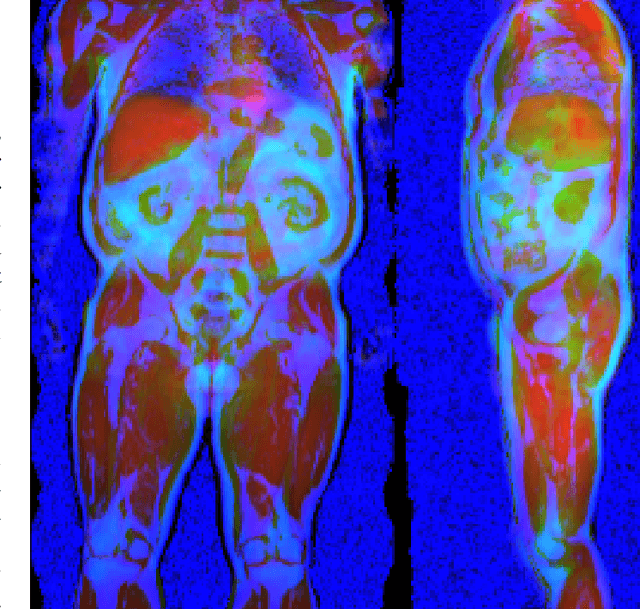
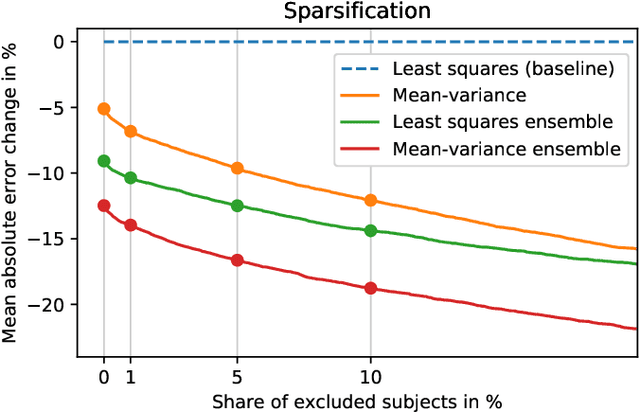
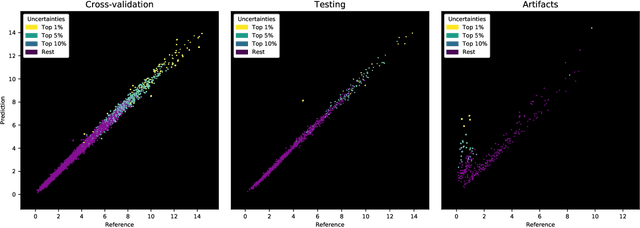
Purpose: To enable fast and automated analysis of body composition from UK Biobank MRI with accurate estimates of individual measurement errors. Methods: In an ongoing large-scale imaging study the UK Biobank has acquired MRI of over 40,000 men and women aged 44-82. Phenotypes derived from these images, such as body composition, can reveal new links between genetics, cardiovascular disease, and metabolic conditions. In this retrospective study, neural networks were trained to provide six measurements of body composition from UK Biobank neck-to-knee body MRI. A ResNet50 architecture can automatically predict these values by image-based regression, but may also produce erroneous outliers. Predictive uncertainty, which could identify these failure cases, was therefore modeled with a mean-variance loss and ensembling. Its estimates of individual prediction errors were evaluated in cross-validation on over 8,000 subjects, tested on another 1,000 cases, and finally applied for inference. Results: Relative measurement errors below 5\% were achieved on all but one target, for intra-class correlation coefficients (ICC) above 0.97 both in validation and testing. Both mean-variance loss and ensembling yielded improvements and provided uncertainty estimates that highlighted some of the worst outlier predictions. Combined, they reached the highest quality, but also exhibited a consistent bias towards high uncertainty in heavyweight subjects. Conclusion: Mean-variance regression and ensembling provided complementary benefits for automated body composition measurements from UK Biobank MRI, reaching high speed and accuracy. These values were inferred for the entire cohort, with uncertainty estimates that can approximate the measurement errors and identify some of the worst outliers automatically.

Approximation of BV functions by neural networks: A regularity theory approach

In this paper we are concerned with the approximation of functions by single hidden layer neural networks with ReLU activation functions on the unit circle. In particular, we are interested in the case when the number of data-points exceeds the number of nodes. We first study the convergence to equilibrium of the stochastic gradient flow associated with the cost function with a quadratic penalization. Specifically, we prove a Poincar\'e inequality for a penalized version of the cost function with explicit constants that are independent of the data and of the number of nodes. As our penalization biases the weights to be bounded, this leads us to study how well a network with bounded weights can approximate a given function of bounded variation (BV). Our main contribution concerning approximation of BV functions, is a result which we call the localization theorem. Specifically, it states that the expected error of the constrained problem, where the length of the weights are less than $R$, is of order $R^{-1/9}$ with respect to the unconstrained problem (the global optimum). The proof is novel in this topic and is inspired by techniques from regularity theory of elliptic partial differential equations. Finally we quantify the expected value of the global optimum by proving a quantitative version of the universal approximation theorem.

Neural ODEs as the Deep Limit of ResNets with constant weights

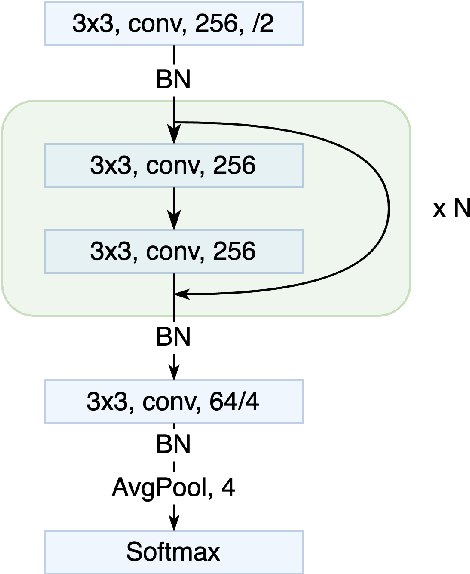
In this paper we prove that, in the deep limit, the stochastic gradient descent on a ResNet type deep neural network, where each layer share the same weight matrix, converges to the stochastic gradient descent for a Neural ODE and that the corresponding value/loss functions converge. Our result gives, in the context of minimization by stochastic gradient descent, a theoretical foundation for considering Neural ODEs as the deep limit of ResNets. Our proof is based on certain decay estimates for associated Fokker-Planck equations.