Deep learning, stochastic gradient descent and diffusion maps

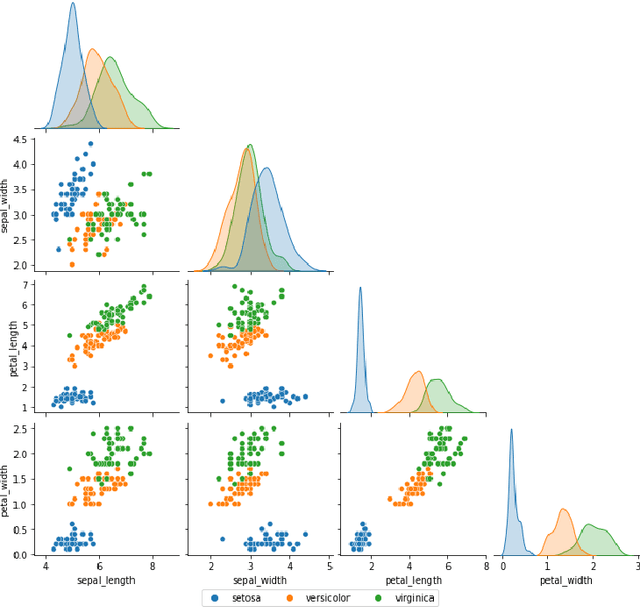
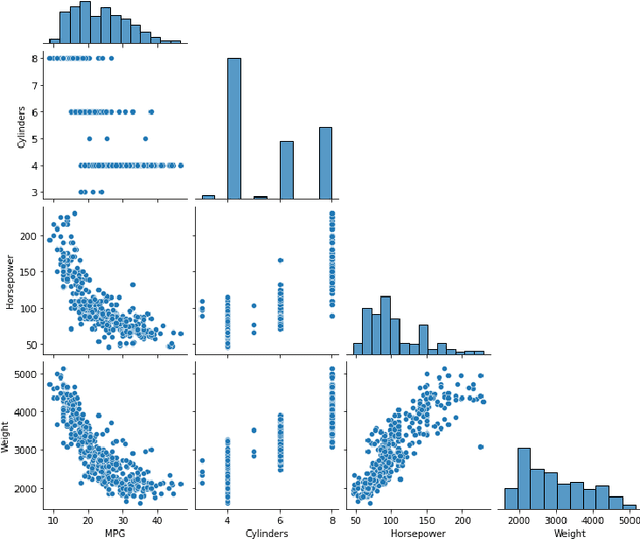
Stochastic gradient descent (SGD) is widely used in deep learning due to its computational efficiency but a complete understanding of why SGD performs so well remains a major challenge. It has been observed empirically that most eigenvalues of the Hessian of the loss functions on the loss landscape of over-parametrized deep networks are close to zero, while only a small number of eigenvalues are large. Zero eigenvalues indicate zero diffusion along the corresponding directions. This indicates that the process of minima selection mainly happens in the relatively low-dimensional subspace corresponding to top eigenvalues of the Hessian. Although the parameter space is very high-dimensional, these findings seems to indicate that the SGD dynamics may mainly live on a low-dimensional manifold. In this paper we pursue a truly data driven approach to the problem of getting a potentially deeper understanding of the high-dimensional parameter surface, and in particular of the landscape traced out by SGD, by analyzing the data generated through SGD, or any other optimizer for that matter, in order to possibly discovery (local) low-dimensional representations of the optimization landscape. As our vehicle for the exploration we use diffusion maps introduced by R. Coifman and coauthors.

Solving the Dirichlet problem for the Monge-Ampère equation using neural networks

The Monge-Amp\`ere equation is a fully nonlinear partial differential equation (PDE) of fundamental importance in analysis, geometry and in the applied sciences. In this paper we solve the Dirichlet problem associated with the Monge-Amp\`ere equation using neural networks and we show that an ansatz using deep input convex neural networks can be used to find the unique convex solution. As part of our analysis we study the effect of singularities and noise in the source function, we consider nontrivial domains, and we investigate how the method performs in higher dimensions. We also compare this method to an alternative approach in which standard feed-forward networks are used together with a loss function which penalizes lack of convexity.

Neural ODEs as the Deep Limit of ResNets with constant weights

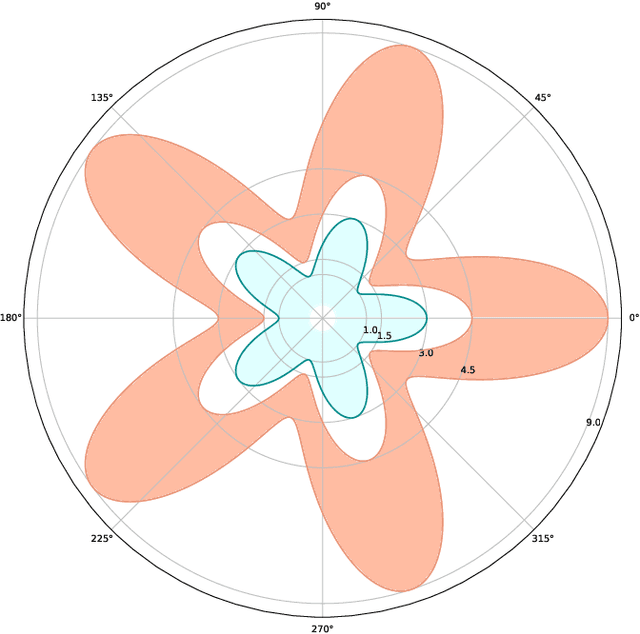
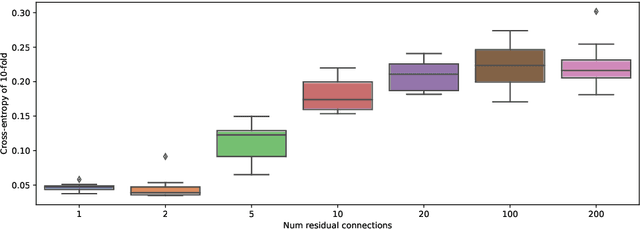
In this paper we prove that, in the deep limit, the stochastic gradient descent on a ResNet type deep neural network, where each layer share the same weight matrix, converges to the stochastic gradient descent for a Neural ODE and that the corresponding value/loss functions converge. Our result gives, in the context of minimization by stochastic gradient descent, a theoretical foundation for considering Neural ODEs as the deep limit of ResNets. Our proof is based on certain decay estimates for associated Fokker-Planck equations.

Neural network augmented inverse problems for PDEs

In this paper we show how to augment classical methods for inverse problems with artificial neural networks. The neural network acts as a prior for the coefficient to be estimated from noisy data. Neural networks are global, smooth function approximators and as such they do not require explicit regularization of the error functional to recover smooth solutions and coefficients. We give detailed examples using the Poisson equation in 1, 2, and 3 space dimensions and show that the neural network augmentation is robust with respect to noisy and incomplete data, mesh, and geometry.

Data-driven discovery of PDEs in complex datasets

Many processes in science and engineering can be described by partial differential equations (PDEs). Traditionally, PDEs are derived by considering first principles of physics to derive the relations between the involved physical quantities of interest. A different approach is to measure the quantities of interest and use deep learning to reverse engineer the PDEs which are describing the physical process. In this paper we use machine learning, and deep learning in particular, to discover PDEs hidden in complex data sets from measurement data. We include examples of data from a known model problem, and real data from weather station measurements. We show how necessary transformations of the input data amounts to coordinate transformations in the discovered PDE, and we elaborate on feature and model selection. It is shown that the dynamics of a non-linear, second order PDE can be accurately described by an ordinary differential equation which is automatically discovered by our deep learning algorithm. Even more interestingly, we show that similar results apply in the context of more complex simulations of the Swedish temperature distribution.

A unified deep artificial neural network approach to partial differential equations in complex geometries

In this paper we use deep feedforward artificial neural networks to approximate solutions to partial differential equations in complex geometries. We show how to modify the backpropagation algorithm to compute the partial derivatives of the network output with respect to the space variables which is needed to approximate the differential operator. The method is based on an ansatz for the solution which requires nothing but feedforward neural networks and an unconstrained gradient based optimization method such as gradient descent or a quasi-Newton method. We show an example where classical mesh based methods cannot be used and neural networks can be seen as an attractive alternative. Finally, we highlight the benefits of deep compared to shallow neural networks and device some other convergence enhancing techniques.