User-to-User Interference Mitigation in Dynamic TDD MIMO Systems with Multi-Antenna Users

We propose a novel method for user-to-user interference (UUI) mitigation in dynamic time-division duplex multiple-input multiple-output communication systems with multi-antenna users. Specifically, we consider the downlink data transmission in the presence of UUI caused by a user that simultaneously transmits in uplink. Our method introduces an overhead for estimation of the user-to-user channels by transmitting pilots from the uplink user to the downlink users. Each downlink user obtains a channel estimate that is used to design a combining matrix for UUI mitigation. We analytically derive an achievable spectral efficiency for the downlink transmission in the presence of UUI with our mitigation technique. Through numerical simulations, we show that our method can significantly improve the spectral efficiency performance in cases of heavy UUI.

Joint Optimization of Switching Point and Power Control in Dynamic TDD Cell-Free Massive MIMO

We consider a cell-free massive multiple-input multiple-output (CFmMIMO) network operating in dynamic time division duplex (DTDD). The switching point between the uplink (UL) and downlink (DL) data transmission phases can be adapted dynamically to the instantaneous quality-of-service (QoS) requirements in order to improve energy efficiency (EE). To this end, we formulate a problem of optimizing the DTDD switching point jointly with the UL and DL power control coefficients, and the large-scale fading decoding (LSFD) weights for EE maximization. Then, we propose an iterative algorithm to solve the formulated challenging problem using successive convex approximation with an approximate stationary solution. Simulation results show that optimizing switching points remarkably improves EE compared with baseline schemes that adjust switching points heuristically.

Exploring Singularities in point clouds with the graph Laplacian: An explicit approach

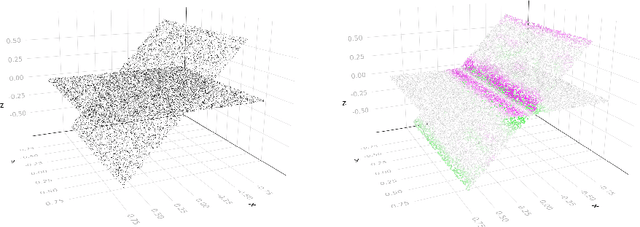
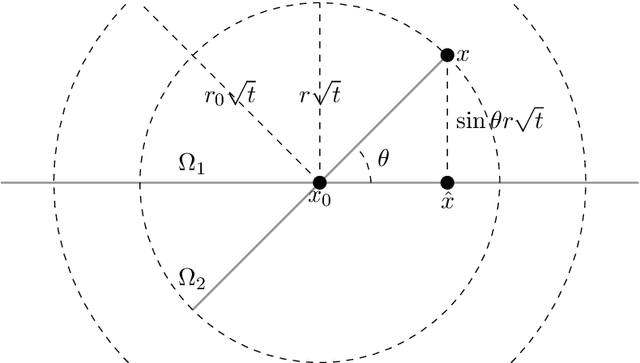
We develop theory and methods that use the graph Laplacian to analyze the geometry of the underlying manifold of point clouds. Our theory provides theoretical guarantees and explicit bounds on the functional form of the graph Laplacian, in the case when it acts on functions defined close to singularities of the underlying manifold. We also propose methods that can be used to estimate these geometric properties of the point cloud, which are based on the theoretical guarantees.

Anytime Coalition Structure Generation with Worst Case Guarantees

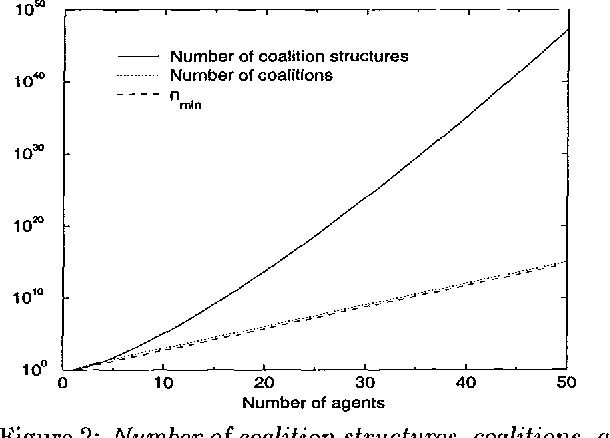
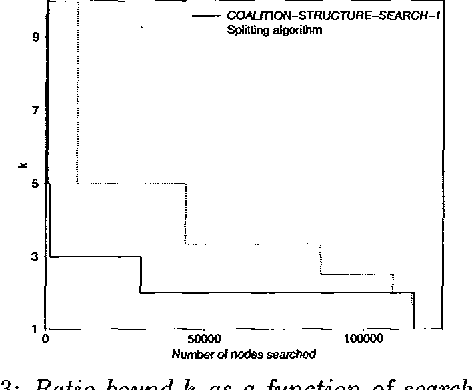
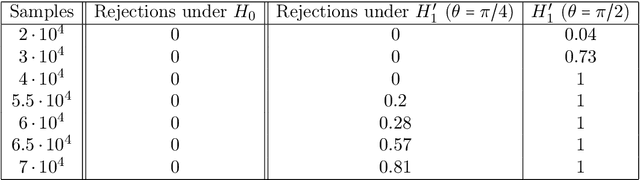
Coalition formation is a key topic in multiagent systems. One would prefer a coalition structure that maximizes the sum of the values of the coalitions, but often the number of coalition structures is too large to allow exhaustive search for the optimal one. But then, can the coalition structure found via a partial search be guaranteed to be within a bound from optimum? We show that none of the previous coalition structure generation algorithms can establish any bound because they search fewer nodes than a threshold that we show necessary for establishing a bound. We present an algorithm that establishes a tight bound within this minimal amount of search, and show that any other algorithm would have to search strictly more. The fraction of nodes needed to be searched approaches zero as the number of agents grows. If additional time remains, our anytime algorithm searches further, and establishes a progressively lower tight bound. Surprisingly, just searching one more node drops the bound in half. As desired, our algorithm lowers the bound rapidly early on, and exhibits diminishing returns to computation. It also drastically outperforms its obvious contenders. Finally, we show how to distribute the desired search across self-interested manipulative agents.