Fernando Tohme
Judgment Aggregation in Multi-Agent Argumentation
Jul 19, 2015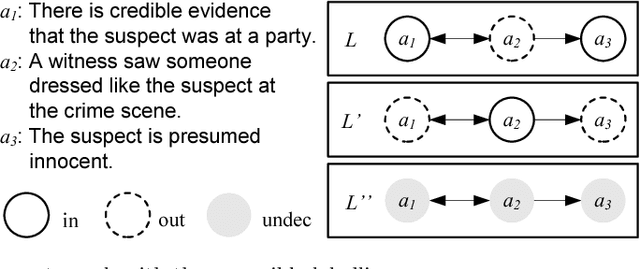
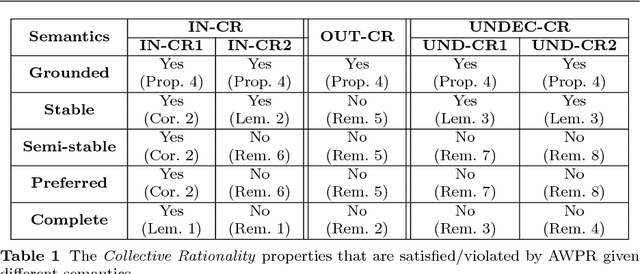
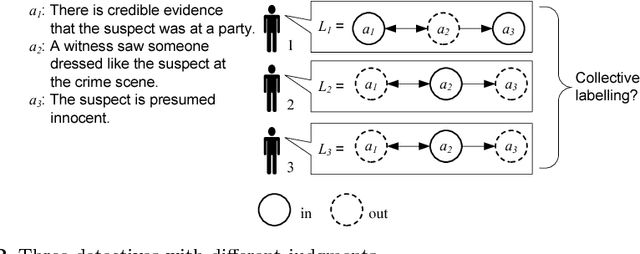
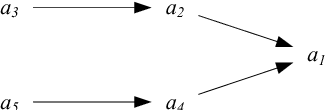
Abstract:Given a set of conflicting arguments, there can exist multiple plausible opinions about which arguments should be accepted, rejected, or deemed undecided. We study the problem of how multiple such judgments can be aggregated. We define the problem by adapting various classical social-choice-theoretic properties for the argumentation domain. We show that while argument-wise plurality voting satisfies many properties, it fails to guarantee the collective rationality of the outcome, and struggles with ties. We then present more general results, proving multiple impossibility results on the existence of any good aggregation operator. After characterising the sufficient and necessary conditions for satisfying collective rationality, we study whether restricting the domain of argument-wise plurality voting to classical semantics allows us to escape the impossibility result. We close by listing graph-theoretic restrictions under which argument-wise plurality rule does produce collectively rational outcomes. In addition to identifying fundamental barriers to collective argument evaluation, our results open up the door for a new research agenda for the argumentation and computational social choice communities.
Anytime Coalition Structure Generation with Worst Case Guarantees
Oct 05, 1998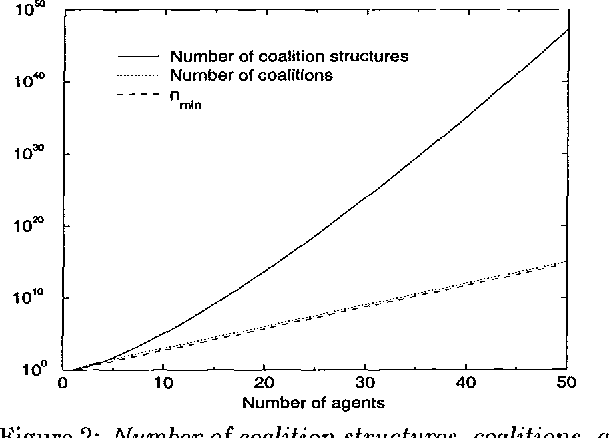
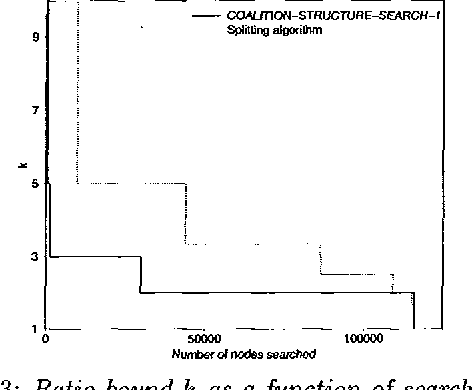
Abstract:Coalition formation is a key topic in multiagent systems. One would prefer a coalition structure that maximizes the sum of the values of the coalitions, but often the number of coalition structures is too large to allow exhaustive search for the optimal one. But then, can the coalition structure found via a partial search be guaranteed to be within a bound from optimum? We show that none of the previous coalition structure generation algorithms can establish any bound because they search fewer nodes than a threshold that we show necessary for establishing a bound. We present an algorithm that establishes a tight bound within this minimal amount of search, and show that any other algorithm would have to search strictly more. The fraction of nodes needed to be searched approaches zero as the number of agents grows. If additional time remains, our anytime algorithm searches further, and establishes a progressively lower tight bound. Surprisingly, just searching one more node drops the bound in half. As desired, our algorithm lowers the bound rapidly early on, and exhibits diminishing returns to computation. It also drastically outperforms its obvious contenders. Finally, we show how to distribute the desired search across self-interested manipulative agents.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge