Who's the Expert? On Multi-source Belief Change

Consider the following belief change/merging scenario. A group of information sources gives a sequence of reports about the state of the world at various instances (e.g. different points in time). The true states at these instances are unknown to us. The sources have varying levels of expertise, also unknown to us, and may be knowledgeable on some topics but not others. This may cause sources to report false statements in areas they lack expertise. What should we believe on the basis of these reports? We provide a framework in which to explore this problem, based on an extension of propositional logic with expertise formulas. This extended language allows us to express beliefs about the state of the world at each instance, as well as beliefs about the expertise of each source. We propose several postulates, provide a couple of families of concrete operators, and analyse these operators with respect to the postulates.

Revision by Conditionals: From Hook to Arrow

The belief revision literature has largely focussed on the issue of how to revise one's beliefs in the light of information regarding matters of fact. Here we turn to an important but comparatively neglected issue: How might one extend a revision operator to handle conditionals as input? Our approach to this question of 'conditional revision' is distinctive insofar as it abstracts from the controversial details of how to revise by factual sentences. We introduce a 'plug and play' method for uniquely extending any iterated belief revision operator to the conditional case. The flexibility of our approach is achieved by having the result of a conditional revision by a Ramsey Test conditional ('arrow') determined by that of a plain revision by its corresponding material conditional ('hook'). It is shown to satisfy a number of new constraints that are of independent interest.

Elementary Iterated Revision and the Levi Identity

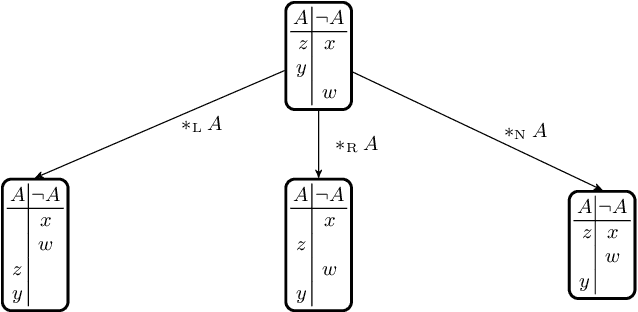
Recent work has considered the problem of extending to the case of iterated belief change the so-called `Harper Identity' (HI), which defines single-shot contraction in terms of single-shot revision. The present paper considers the prospects of providing a similar extension of the Levi Identity (LI), in which the direction of definition runs the other way. We restrict our attention here to the three classic iterated revision operators--natural, restrained and lexicographic, for which we provide here the first collective characterisation in the literature, under the appellation of `elementary' operators. We consider two prima facie plausible ways of extending (LI). The first proposal involves the use of the rational closure operator to offer a `reductive' account of iterated revision in terms of iterated contraction. The second, which doesn't commit to reductionism, was put forward some years ago by Nayak et al. We establish that, for elementary revision operators and under mild assumptions regarding contraction, Nayak's proposal is equivalent to a new set of postulates formalising the claim that contraction by $\neg A$ should be considered to be a kind of `mild' revision by $A$. We then show that these, in turn, under slightly weaker assumptions, jointly amount to the conjunction of a pair of constraints on the extension of (HI) that were recently proposed in the literature. Finally, we consider the consequences of endorsing both suggestions and show that this would yield an identification of rational revision with natural revision. We close the paper by discussing the general prospects for defining iterated revision in terms of iterated contraction.

On Rational Entailment for Propositional Typicality Logic

Propositional Typicality Logic (PTL) is a recently proposed logic, obtained by enriching classical propositional logic with a typicality operator capturing the most typical (alias normal or conventional) situations in which a given sentence holds. The semantics of PTL is in terms of ranked models as studied in the well-known KLM approach to preferential reasoning and therefore KLM-style rational consequence relations can be embedded in PTL. In spite of the non-monotonic features introduced by the semantics adopted for the typicality operator, the obvious Tarskian definition of entailment for PTL remains monotonic and is therefore not appropriate in many contexts. Our first important result is an impossibility theorem showing that a set of proposed postulates that at first all seem appropriate for a notion of entailment with regard to typicality cannot be satisfied simultaneously. Closer inspection reveals that this result is best interpreted as an argument for advocating the development of more than one type of PTL entailment. In the spirit of this interpretation, we investigate three different (semantic) versions of entailment for PTL, each one based on the definition of rational closure as introduced by Lehmann and Magidor for KLM-style conditionals, and constructed using different notions of minimality.

On Strengthening the Logic of Iterated Belief Revision: Proper Ordinal Interval Operators

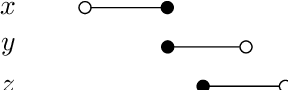
Darwiche and Pearl's seminal 1997 article outlined a number of baseline principles for a logic of iterated belief revision. These principles, the DP postulates, have been supplemented in a number of alternative ways. Most of the suggestions made have resulted in a form of `reductionism' that identifies belief states with orderings of worlds. However, this position has recently been criticised as being unacceptably strong. Other proposals, such as the popular principle (P), aka `Independence', characteristic of `admissible' revision operators, remain commendably more modest. In this paper, we supplement both the DP postulates and (P) with a number of novel conditions. While the DP postulates constrain the relation between a prior and a posterior conditional belief set, our new principles notably govern the relation between two posterior conditional belief sets obtained from a common prior by different revisions. We show that operators from the resulting family, which subsumes both lexicographic and restrained revision, can be represented as relating belief states that are associated with a `proper ordinal interval' (POI) assignment, a structure more fine-grained than a simple ordering of worlds. We close the paper by noting that these operators satisfy iterated versions of a large number of AGM era postulates, including Superexpansion, that are not sound for admissible operators in general.

Extending the Harper Identity to Iterated Belief Change

The field of iterated belief change has focused mainly on revision, with the other main operator of AGM belief change theory, i.e. contraction, receiving relatively little attention. In this paper we extend the Harper Identity from single-step change to define iterated contraction in terms of iterated revision. Specifically, just as the Harper Identity provides a recipe for defining the belief set resulting from contracting A in terms of (i) the initial belief set and (ii) the belief set resulting from revision by not-A, we look at ways to define the plausibility ordering over worlds resulting from contracting A in terms of (iii) the initial plausibility ordering, and (iv) the plausibility ordering resulting from revision by not-A. After noting that the most straightforward such extension leads to a trivialisation of the space of permissible orderings, we provide a family of operators for combining plausibility orderings that avoid such a result. These operators are characterised in our domain of interest by a pair of intuitively compelling properties, which turn out to enable the derivation of a number of iterated contraction postulates from postulates for iterated revision. We finish by observing that a salient member of this family allows for the derivation of counterparts for contraction of some well known iterated revision operators, as well as for defining new iterated contraction operators.

Judgment Aggregation in Multi-Agent Argumentation

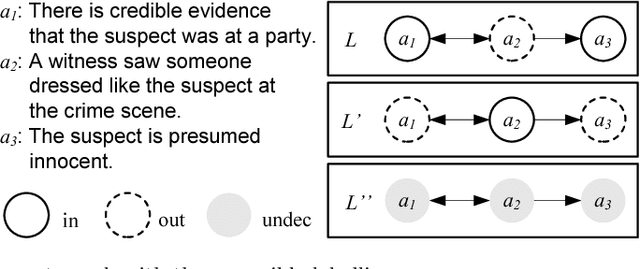
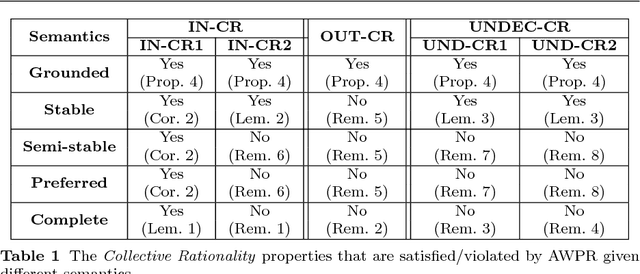
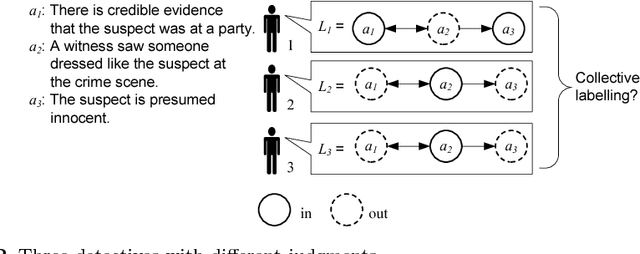
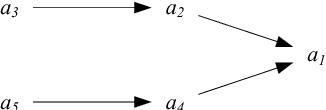
Given a set of conflicting arguments, there can exist multiple plausible opinions about which arguments should be accepted, rejected, or deemed undecided. We study the problem of how multiple such judgments can be aggregated. We define the problem by adapting various classical social-choice-theoretic properties for the argumentation domain. We show that while argument-wise plurality voting satisfies many properties, it fails to guarantee the collective rationality of the outcome, and struggles with ties. We then present more general results, proving multiple impossibility results on the existence of any good aggregation operator. After characterising the sufficient and necessary conditions for satisfying collective rationality, we study whether restricting the domain of argument-wise plurality voting to classical semantics allows us to escape the impossibility result. We close by listing graph-theoretic restrictions under which argument-wise plurality rule does produce collectively rational outcomes. In addition to identifying fundamental barriers to collective argument evaluation, our results open up the door for a new research agenda for the argumentation and computational social choice communities.

Abduction and Dialogical Proof in Argumentation and Logic Programming

We develop a model of abduction in abstract argumentation, where changes to an argumentation framework act as hypotheses to explain the support of an observation. We present dialogical proof theories for the main decision problems (i.e., finding hypothe- ses that explain skeptical/credulous support) and we show that our model can be instantiated on the basis of abductive logic programs.

On the Link between Partial Meet, Kernel, and Infra Contraction and its Application to Horn Logic

Standard belief change assumes an underlying logic containing full classical propositional logic. However, there are good reasons for considering belief change in less expressive logics as well. In this paper we build on recent investigations by Delgrande on contraction for Horn logic. We show that the standard basic form of contraction, partial meet, is too strong in the Horn case. This result stands in contrast to Delgrande's conjecture that orderly maxichoice is the appropriate form of contraction for Horn logic. We then define a more appropriate notion of basic contraction for the Horn case, influenced by the convexity property holding for full propositional logic and which we refer to as infra contraction. The main contribution of this work is a result which shows that the construction method for Horn contraction for belief sets based on our infra remainder sets corresponds exactly to Hansson's classical kernel contraction for belief sets, when restricted to Horn logic. This result is obtained via a detour through contraction for belief bases. We prove that kernel contraction for belief bases produces precisely the same results as the belief base version of infra contraction. The use of belief bases to obtain this result provides evidence for the conjecture that Horn belief change is best viewed as a hybrid version of belief set change and belief base change. One of the consequences of the link with base contraction is the provision of a representation result for Horn contraction for belief sets in which a version of the Core-retainment postulate features.

On revising fuzzy belief bases

We look at the problem of revising fuzzy belief bases, i.e., belief base revision in which both formulas in the base as well as revision-input formulas can come attached with varying truth-degrees. Working within a very general framework for fuzzy logic which is able to capture a variety of types of inference under uncertainty, such as truth-functional fuzzy logics and certain types of probabilistic inference, we show how the idea of rational change from 'crisp' base revision, as embodied by the idea of partial meet revision, can be faithfully extended to revising fuzzy belief bases. We present and axiomatise an operation of partial meet fuzzy revision and illustrate how the operation works in several important special instances of the framework.