Jake Chandler
Revision by Conditionals: From Hook to Arrow
Jun 29, 2020



Abstract:The belief revision literature has largely focussed on the issue of how to revise one's beliefs in the light of information regarding matters of fact. Here we turn to an important but comparatively neglected issue: How might one extend a revision operator to handle conditionals as input? Our approach to this question of 'conditional revision' is distinctive insofar as it abstracts from the controversial details of how to revise by factual sentences. We introduce a 'plug and play' method for uniquely extending any iterated belief revision operator to the conditional case. The flexibility of our approach is achieved by having the result of a conditional revision by a Ramsey Test conditional ('arrow') determined by that of a plain revision by its corresponding material conditional ('hook'). It is shown to satisfy a number of new constraints that are of independent interest.
Elementary Iterated Revision and the Levi Identity
Jul 02, 2019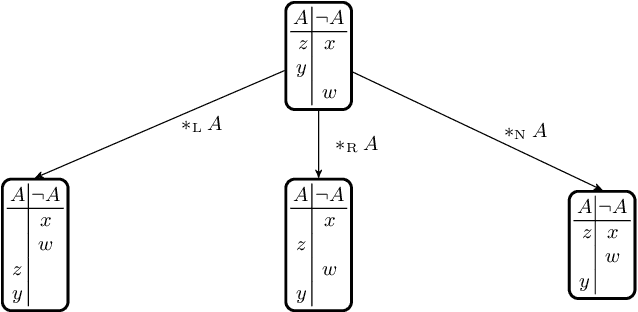

Abstract:Recent work has considered the problem of extending to the case of iterated belief change the so-called `Harper Identity' (HI), which defines single-shot contraction in terms of single-shot revision. The present paper considers the prospects of providing a similar extension of the Levi Identity (LI), in which the direction of definition runs the other way. We restrict our attention here to the three classic iterated revision operators--natural, restrained and lexicographic, for which we provide here the first collective characterisation in the literature, under the appellation of `elementary' operators. We consider two prima facie plausible ways of extending (LI). The first proposal involves the use of the rational closure operator to offer a `reductive' account of iterated revision in terms of iterated contraction. The second, which doesn't commit to reductionism, was put forward some years ago by Nayak et al. We establish that, for elementary revision operators and under mild assumptions regarding contraction, Nayak's proposal is equivalent to a new set of postulates formalising the claim that contraction by $\neg A$ should be considered to be a kind of `mild' revision by $A$. We then show that these, in turn, under slightly weaker assumptions, jointly amount to the conjunction of a pair of constraints on the extension of (HI) that were recently proposed in the literature. Finally, we consider the consequences of endorsing both suggestions and show that this would yield an identification of rational revision with natural revision. We close the paper by discussing the general prospects for defining iterated revision in terms of iterated contraction.
On Strengthening the Logic of Iterated Belief Revision: Proper Ordinal Interval Operators
Jul 26, 2018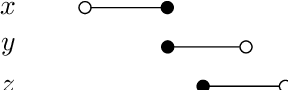

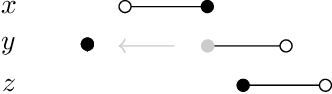
Abstract:Darwiche and Pearl's seminal 1997 article outlined a number of baseline principles for a logic of iterated belief revision. These principles, the DP postulates, have been supplemented in a number of alternative ways. Most of the suggestions made have resulted in a form of `reductionism' that identifies belief states with orderings of worlds. However, this position has recently been criticised as being unacceptably strong. Other proposals, such as the popular principle (P), aka `Independence', characteristic of `admissible' revision operators, remain commendably more modest. In this paper, we supplement both the DP postulates and (P) with a number of novel conditions. While the DP postulates constrain the relation between a prior and a posterior conditional belief set, our new principles notably govern the relation between two posterior conditional belief sets obtained from a common prior by different revisions. We show that operators from the resulting family, which subsumes both lexicographic and restrained revision, can be represented as relating belief states that are associated with a `proper ordinal interval' (POI) assignment, a structure more fine-grained than a simple ordering of worlds. We close the paper by noting that these operators satisfy iterated versions of a large number of AGM era postulates, including Superexpansion, that are not sound for admissible operators in general.
Extending the Harper Identity to Iterated Belief Change
Apr 19, 2016Abstract:The field of iterated belief change has focused mainly on revision, with the other main operator of AGM belief change theory, i.e. contraction, receiving relatively little attention. In this paper we extend the Harper Identity from single-step change to define iterated contraction in terms of iterated revision. Specifically, just as the Harper Identity provides a recipe for defining the belief set resulting from contracting A in terms of (i) the initial belief set and (ii) the belief set resulting from revision by not-A, we look at ways to define the plausibility ordering over worlds resulting from contracting A in terms of (iii) the initial plausibility ordering, and (iv) the plausibility ordering resulting from revision by not-A. After noting that the most straightforward such extension leads to a trivialisation of the space of permissible orderings, we provide a family of operators for combining plausibility orderings that avoid such a result. These operators are characterised in our domain of interest by a pair of intuitively compelling properties, which turn out to enable the derivation of a number of iterated contraction postulates from postulates for iterated revision. We finish by observing that a salient member of this family allows for the derivation of counterparts for contraction of some well known iterated revision operators, as well as for defining new iterated contraction operators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge