Region-Based Merging of Open-Domain Terminological Knowledge

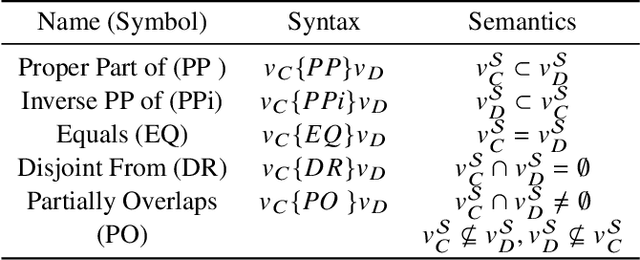
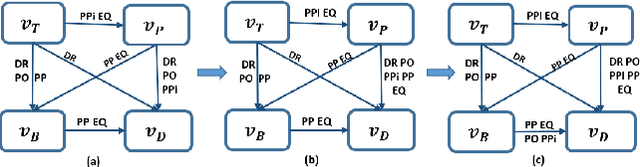
This paper introduces a novel method for merging open-domain terminological knowledge. It takes advantage of the Region Connection Calculus (RCC5), a formalism used to represent regions in a topological space and to reason about their set-theoretic relationships. To this end, we first propose a faithful translation of terminological knowledge provided by several and potentially conflicting sources into region spaces. The merging is then performed on these spaces, and the result is translated back into the underlying language of the input sources. Our approach allows us to benefit from the expressivity and the flexibility of RCC5 while dealing with conflicting knowledge in a principled way.

Situated Conditional Reasoning

Conditionals are useful for modelling, but are not always sufficiently expressive for capturing information accurately. In this paper we make the case for a form of conditional that is situation-based. These conditionals are more expressive than classical conditionals, are general enough to be used in several application domains, and are able to distinguish, for example, between expectations and counterfactuals. Formally, they are shown to generalise the conditional setting in the style of Kraus, Lehmann, and Magidor. We show that situation-based conditionals can be described in terms of a set of rationality postulates. We then propose an intuitive semantics for these conditionals, and present a representation result which shows that our semantic construction corresponds exactly to the description in terms of postulates. With the semantics in place, we proceed to define a form of entailment for situated conditional knowledge bases, which we refer to as minimal closure. It is reminiscent of and, indeed, inspired by, the version of entailment for propositional conditional knowledge bases known as rational closure. Finally, we proceed to show that it is possible to reduce the computation of minimal closure to a series of propositional entailment and satisfiability checks. While this is also the case for rational closure, it is somewhat surprising that the result carries over to minimal closure.

Theoretical Foundations of Defeasible Description Logics

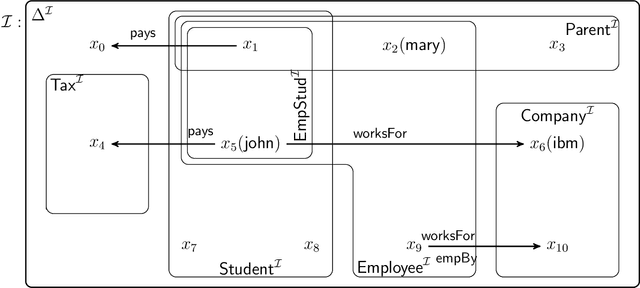
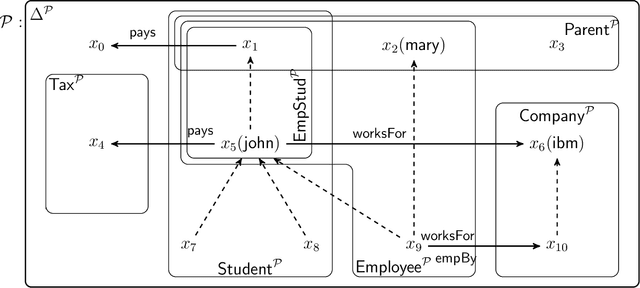
We extend description logics (DLs) with non-monotonic reasoning features. We start by investigating a notion of defeasible subsumption in the spirit of defeasible conditionals as studied by Kraus, Lehmann and Magidor in the propositional case. In particular, we consider a natural and intuitive semantics for defeasible subsumption, and investigate KLM-style syntactic properties for both preferential and rational subsumption. Our contribution includes two representation results linking our semantic constructions to the set of preferential and rational properties considered. Besides showing that our semantics is appropriate, these results pave the way for more effective decision procedures for defeasible reasoning in DLs. Indeed, we also analyse the problem of non-monotonic reasoning in DLs at the level of entailment and present an algorithm for the computation of rational closure of a defeasible ontology. Importantly, our algorithm relies completely on classical entailment and shows that the computational complexity of reasoning over defeasible ontologies is no worse than that of reasoning in the underlying classical DL ALC.

On Rational Entailment for Propositional Typicality Logic

Propositional Typicality Logic (PTL) is a recently proposed logic, obtained by enriching classical propositional logic with a typicality operator capturing the most typical (alias normal or conventional) situations in which a given sentence holds. The semantics of PTL is in terms of ranked models as studied in the well-known KLM approach to preferential reasoning and therefore KLM-style rational consequence relations can be embedded in PTL. In spite of the non-monotonic features introduced by the semantics adopted for the typicality operator, the obvious Tarskian definition of entailment for PTL remains monotonic and is therefore not appropriate in many contexts. Our first important result is an impossibility theorem showing that a set of proposed postulates that at first all seem appropriate for a notion of entailment with regard to typicality cannot be satisfied simultaneously. Closer inspection reveals that this result is best interpreted as an argument for advocating the development of more than one type of PTL entailment. In the spirit of this interpretation, we investigate three different (semantic) versions of entailment for PTL, each one based on the definition of rational closure as introduced by Lehmann and Magidor for KLM-style conditionals, and constructed using different notions of minimality.

On the Link between Partial Meet, Kernel, and Infra Contraction and its Application to Horn Logic

Standard belief change assumes an underlying logic containing full classical propositional logic. However, there are good reasons for considering belief change in less expressive logics as well. In this paper we build on recent investigations by Delgrande on contraction for Horn logic. We show that the standard basic form of contraction, partial meet, is too strong in the Horn case. This result stands in contrast to Delgrande's conjecture that orderly maxichoice is the appropriate form of contraction for Horn logic. We then define a more appropriate notion of basic contraction for the Horn case, influenced by the convexity property holding for full propositional logic and which we refer to as infra contraction. The main contribution of this work is a result which shows that the construction method for Horn contraction for belief sets based on our infra remainder sets corresponds exactly to Hansson's classical kernel contraction for belief sets, when restricted to Horn logic. This result is obtained via a detour through contraction for belief bases. We prove that kernel contraction for belief bases produces precisely the same results as the belief base version of infra contraction. The use of belief bases to obtain this result provides evidence for the conjecture that Horn belief change is best viewed as a hybrid version of belief set change and belief base change. One of the consequences of the link with base contraction is the provision of a representation result for Horn contraction for belief sets in which a version of the Core-retainment postulate features.

Action Theory Evolution

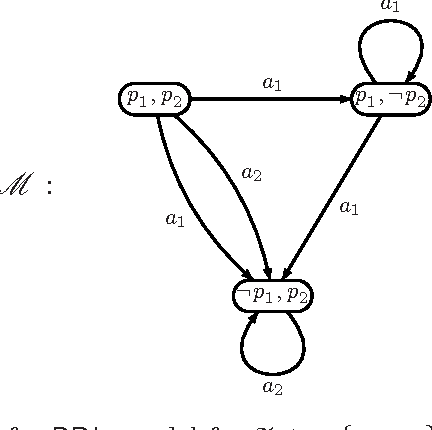
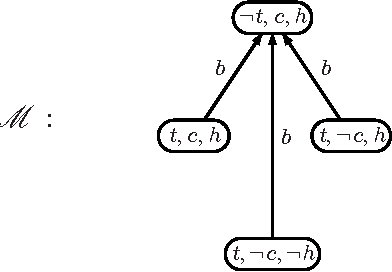
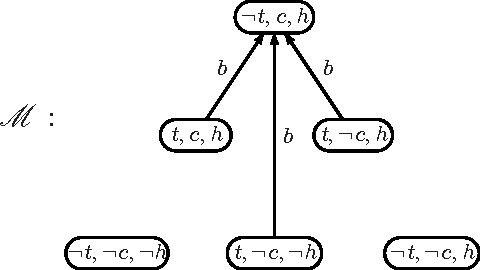
Like any other logical theory, domain descriptions in reasoning about actions may evolve, and thus need revision methods to adequately accommodate new information about the behavior of actions. The present work is about changing action domain descriptions in propositional dynamic logic. Its contribution is threefold: first we revisit the semantics of action theory contraction that has been done in previous work, giving more robust operators that express minimal change based on a notion of distance between Kripke-models. Second we give algorithms for syntactical action theory contraction and establish their correctness w.r.t. our semantics. Finally we state postulates for action theory contraction and assess the behavior of our operators w.r.t. them. Moreover, we also address the revision counterpart of action theory change, showing that it benefits from our semantics for contraction.

Metatheory of actions: beyond consistency

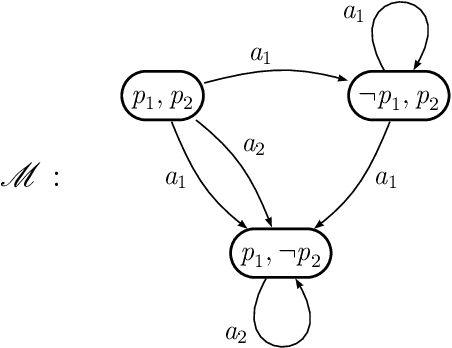
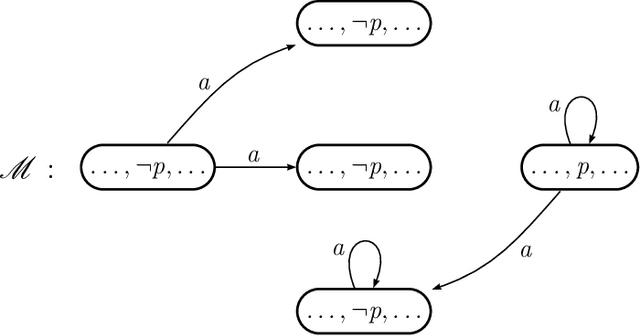
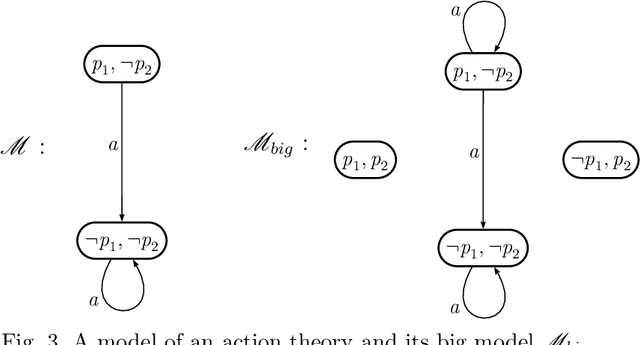
Consistency check has been the only criterion for theory evaluation in logic-based approaches to reasoning about actions. This work goes beyond that and contributes to the metatheory of actions by investigating what other properties a good domain description in reasoning about actions should have. We state some metatheoretical postulates concerning this sore spot. When all postulates are satisfied together we have a modular action theory. Besides being easier to understand and more elaboration tolerant in McCarthy's sense, modular theories have interesting properties. We point out the problems that arise when the postulates about modularity are violated and propose algorithmic checks that can help the designer of an action theory to overcome them.