Belief Change based on Knowledge Measures

Knowledge Measures (KMs) aim at quantifying the amount of knowledge/information that a knowledge base carries. On the other hand, Belief Change (BC) is the process of changing beliefs (in our case, in terms of contraction, expansion and revision) taking into account a new piece of knowledge, which possibly may be in contradiction with the current belief. We propose a new quantitative BC framework that is based on KMs by defining belief change operators that try to minimise, from an information-theoretic point of view, the surprise that the changed belief carries. To this end, we introduce the principle of minimal surprise. In particular, our contributions are (i) a general information-theoretic approach to KMs for which [1] is a special case; (ii) KM-based BC operators that satisfy the so-called AGM postulates; and (iii) a characterisation of any BC operator that satisfies the AGM postulates as a KM-based BC operator, i.e., any BC operator satisfying the AGM postulates can be encoded within our quantitative BC framework. We also introduce quantitative measures that account for the information loss of contraction, information gain of expansion and information change of revision. We also give a succinct look into the problem of iterated revision, which deals with the application of a sequence of revision operations in our framework, and also illustrate how one may build from our KM-based contraction operator also one not satisfying the (in)famous recovery postulate, by focusing on the so-called severe withdrawal model as an illustrative example.

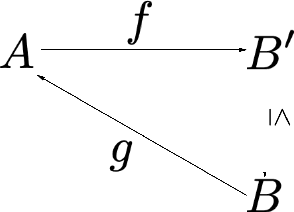
A General Framework for Modelling Conditional Reasoning -- Preliminary Report

We introduce and investigate here a formalisation for conditionals that allows the definition of a broad class of reasoning systems. This framework covers the most popular kinds of conditional reasoning in logic-based KR: the semantics we propose is appropriate for a structural analysis of those conditionals that do not satisfy closure properties associated to classical logics.

A Minimal Deductive System for RDFS with Negative Statements

The triple language RDFS is designed to represent and reason with \emph{positive} statements only (e.g."antipyretics are drugs"). In this paper we show how to extend RDFS to express and reason with various forms of negative statements under the Open World Assumption (OWA). To do so, we start from $\rho df$, a minimal, but significant RDFS fragment that covers all essential features of RDFS, and then extend it to $\rho df_\bot^\neg$, allowing express also statements such as "radio therapies are non drug treatments", "Ebola has no treatment", or "opioids and antipyretics are disjoint classes". The main and, to the best of our knowledge, unique features of our proposal are: (i) $\rho df_\bot^\neg$ remains syntactically a triple language by extending $\rho df$ with new symbols with specific semantics and there is no need to revert to the reification method to represent negative triples; (ii) the logic is defined in such a way that any RDFS reasoner/store may handle the new predicates as ordinary terms if it does not want to take account of the extra capabilities; (iii) despite negated statements, every $\rho df_\bot^\neg$ knowledge base is satisfiable; (iv) the $\rho df_\bot^\neg$ entailment decision procedure is obtained from $\rho df$ via additional inference rules favouring a potential implementation; and (v) deciding entailment in $\rho df_\bot^\neg$ ranges from P to NP.

Situated Conditional Reasoning

Conditionals are useful for modelling, but are not always sufficiently expressive for capturing information accurately. In this paper we make the case for a form of conditional that is situation-based. These conditionals are more expressive than classical conditionals, are general enough to be used in several application domains, and are able to distinguish, for example, between expectations and counterfactuals. Formally, they are shown to generalise the conditional setting in the style of Kraus, Lehmann, and Magidor. We show that situation-based conditionals can be described in terms of a set of rationality postulates. We then propose an intuitive semantics for these conditionals, and present a representation result which shows that our semantic construction corresponds exactly to the description in terms of postulates. With the semantics in place, we proceed to define a form of entailment for situated conditional knowledge bases, which we refer to as minimal closure. It is reminiscent of and, indeed, inspired by, the version of entailment for propositional conditional knowledge bases known as rational closure. Finally, we proceed to show that it is possible to reduce the computation of minimal closure to a series of propositional entailment and satisfiability checks. While this is also the case for rational closure, it is somewhat surprising that the result carries over to minimal closure.

A Rational Entailment for Expressive Description Logics via Description Logic Programs

Lehmann and Magidor's rational closure is acknowledged as a landmark in the field of non-monotonic logics and it has also been re-formulated in the context of Description Logics (DLs). We show here how to model a rational form of entailment for expressive DLs, such as SROIQ, providing a novel reasoning procedure that compiles a non-monotone DL knowledge base into a description logic program (dl-program).

Defeasible RDFS via Rational Closure

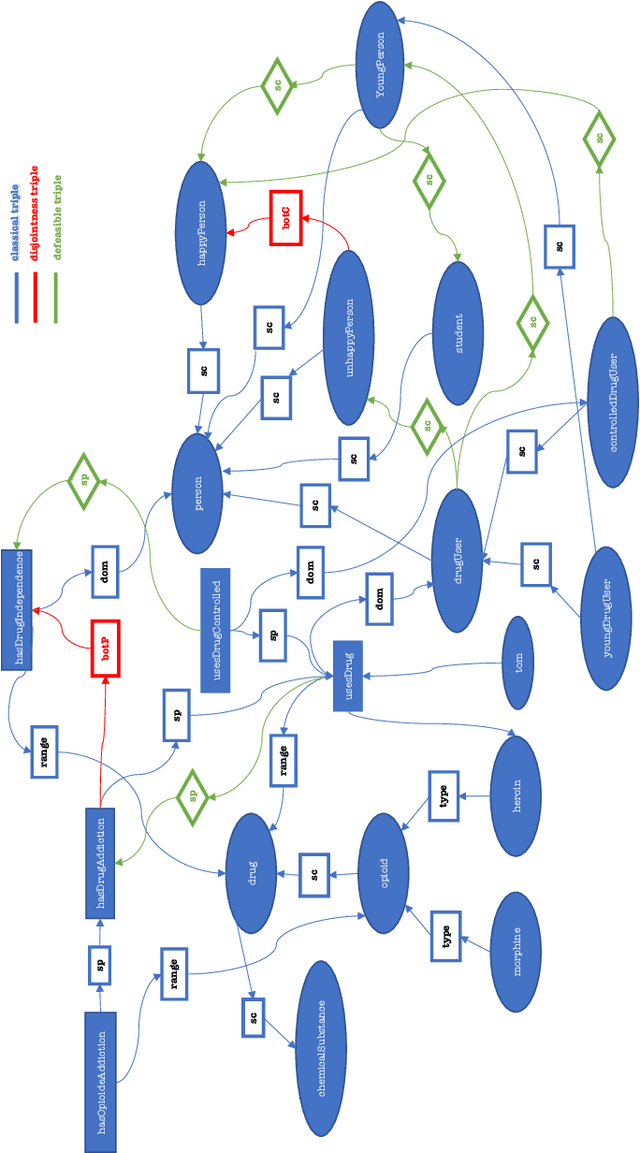
In the field of non-monotonic logics, the notion of Rational Closure (RC) is acknowledged as a prominent approach. In recent years, RC has gained even more popularity in the context of Description Logics (DLs), the logic underpinning the semantic web standard ontology language OWL 2, whose main ingredients are classes and roles. In this work, we show how to integrate RC within the triple language RDFS, which together with OWL2 are the two major standard semantic web ontology languages. To do so, we start from $\rho df$, which is the logic behind RDFS, and then extend it to $\rho df_\bot$, allowing to state that two entities are incompatible. Eventually, we propose defeasible $\rho df_\bot$ via a typical RC construction. The main features of our approach are: (i) unlike most other approaches that add an extra non-monotone rule layer on top of monotone RDFS, defeasible $\rho df_\bot$ remains syntactically a triple language and is a simple extension of $\rho df_\bot$ by introducing some new predicate symbols with specific semantics. In particular, any RDFS reasoner/store may handle them as ordinary terms if it does not want to take account for the extra semantics of the new predicate symbols; (ii) the defeasible $\rho df_\bot$ entailment decision procedure is build on top of the $\rho df_\bot$ entailment decision procedure, which in turn is an extension of the one for $\rho df$ via some additional inference rules favouring an potential implementation; and (iii) defeasible $\rho df_\bot$ entailment can be decided in polynomial time.

Theoretical Foundations of Defeasible Description Logics

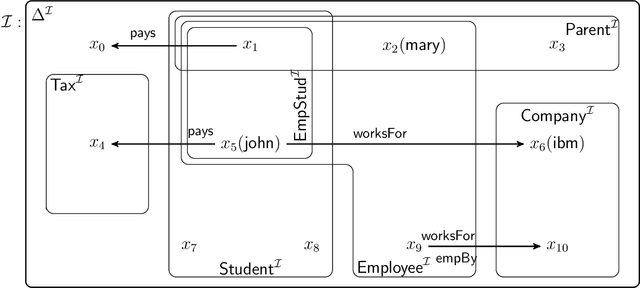
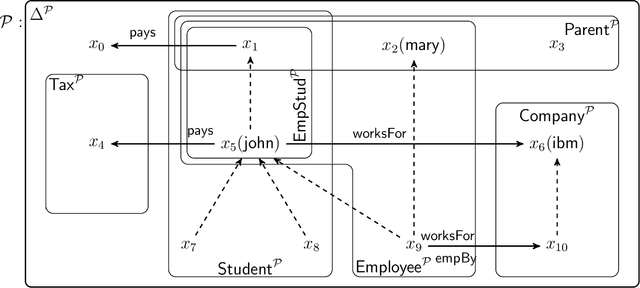
We extend description logics (DLs) with non-monotonic reasoning features. We start by investigating a notion of defeasible subsumption in the spirit of defeasible conditionals as studied by Kraus, Lehmann and Magidor in the propositional case. In particular, we consider a natural and intuitive semantics for defeasible subsumption, and investigate KLM-style syntactic properties for both preferential and rational subsumption. Our contribution includes two representation results linking our semantic constructions to the set of preferential and rational properties considered. Besides showing that our semantics is appropriate, these results pave the way for more effective decision procedures for defeasible reasoning in DLs. Indeed, we also analyse the problem of non-monotonic reasoning in DLs at the level of entailment and present an algorithm for the computation of rational closure of a defeasible ontology. Importantly, our algorithm relies completely on classical entailment and shows that the computational complexity of reasoning over defeasible ontologies is no worse than that of reasoning in the underlying classical DL ALC.

On Rational Entailment for Propositional Typicality Logic

Propositional Typicality Logic (PTL) is a recently proposed logic, obtained by enriching classical propositional logic with a typicality operator capturing the most typical (alias normal or conventional) situations in which a given sentence holds. The semantics of PTL is in terms of ranked models as studied in the well-known KLM approach to preferential reasoning and therefore KLM-style rational consequence relations can be embedded in PTL. In spite of the non-monotonic features introduced by the semantics adopted for the typicality operator, the obvious Tarskian definition of entailment for PTL remains monotonic and is therefore not appropriate in many contexts. Our first important result is an impossibility theorem showing that a set of proposed postulates that at first all seem appropriate for a notion of entailment with regard to typicality cannot be satisfied simultaneously. Closer inspection reveals that this result is best interpreted as an argument for advocating the development of more than one type of PTL entailment. In the spirit of this interpretation, we investigate three different (semantic) versions of entailment for PTL, each one based on the definition of rational closure as introduced by Lehmann and Magidor for KLM-style conditionals, and constructed using different notions of minimality.

A Polynomial Time Subsumption Algorithm for Nominal Safe $\mathcal{ELO}_\bot$ under Rational Closure

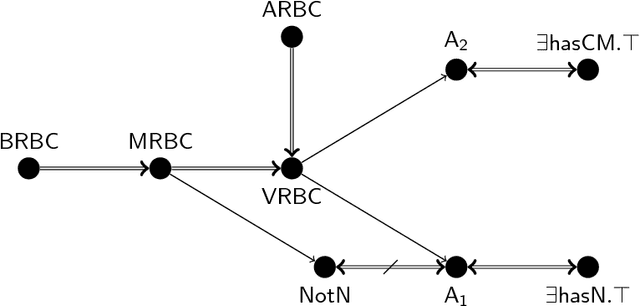
Description Logics (DLs) under Rational Closure (RC) is a well-known framework for non-monotonic reasoning in DLs. In this paper, we address the concept subsumption decision problem under RC for nominal safe $\mathcal{ELO}_\bot$, a notable and practically important DL representative of the OWL 2 profile OWL 2 EL. Our contribution here is to define a polynomial time subsumption procedure for nominal safe $\mathcal{ELO}_\bot$ under RC that relies entirely on a series of classical, monotonic $\mathcal{EL}_\bot$ subsumption tests. Therefore, any existing classical monotonic $\mathcal{EL}_\bot$ reasoner can be used as a black box to implement our method. We then also adapt the method to one of the known extensions of RC for DLs, namely Defeasible Inheritance-based DLs without losing the computational tractability.

Revising Incompletely Specified Convex Probabilistic Belief Bases

We propose a method for an agent to revise its incomplete probabilistic beliefs when a new piece of propositional information is observed. In this work, an agent's beliefs are represented by a set of probabilistic formulae -- a belief base. The method involves determining a representative set of 'boundary' probability distributions consistent with the current belief base, revising each of these probability distributions and then translating the revised information into a new belief base. We use a version of Lewis Imaging as the revision operation. The correctness of the approach is proved. The expressivity of the belief bases under consideration are rather restricted, but has some applications. We also discuss methods of belief base revision employing the notion of optimum entropy, and point out some of the benefits and difficulties in those methods. Both the boundary distribution method and the optimum entropy method are reasonable, yet yield different results.