Non-monotonic Extensions to Formal Concept Analysis via Object Preferences

Formal Concept Analysis (FCA) is an approach to creating a conceptual hierarchy in which a \textit{concept lattice} is generated from a \textit{formal context}. That is, a triple consisting of a set of objects, $G$, a set of attributes, $M$, and an incidence relation $I$ on $G \times M$. A \textit{concept} is then modelled as a pair consisting of a set of objects (the \textit{extent}), and a set of shared attributes (the \textit{intent}). Implications in FCA describe how one set of attributes follows from another. The semantics of these implications closely resemble that of logical consequence in classical logic. In that sense, it describes a monotonic conditional. The contributions of this paper are two-fold. First, we introduce a non-monotonic conditional between sets of attributes, which assumes a preference over the set of objects. We show that this conditional gives rise to a consequence relation that is consistent with the postulates for non-monotonicty proposed by Kraus, Lehmann, and Magidor (commonly referred to as the KLM postulates). We argue that our contribution establishes a strong characterisation of non-monotonicity in FCA. Typical concepts represent concepts where the intent aligns with expectations from the extent, allowing for an exception-tolerant view of concepts. To this end, we show that the set of all typical concepts is a meet semi-lattice of the original concept lattice. This notion of typical concepts is a further introduction of KLM-style typicality into FCA, and is foundational towards developing an algebraic structure representing a concept lattice of prototypical concepts.

Towards Propositional KLM-Style Defeasible Standpoint Logics

The KLM approach to defeasible reasoning introduces a weakened form of implication into classical logic. This allows one to incorporate exceptions to general rules into a logical system, and for old conclusions to be withdrawn upon learning new contradictory information. Standpoint logics are a group of logics, introduced to the field of Knowledge Representation in the last 5 years, which allow for multiple viewpoints to be integrated into the same ontology, even when certain viewpoints may hold contradicting beliefs. In this paper, we aim to integrate standpoints into KLM propositional logic in a restricted setting. We introduce the logical system of Defeasible Restricted Standpoint Logic (DRSL) and define its syntax and semantics. Specifically, we integrate ranked interpretations and standpoint structures, which provide the semantics for propositional KLM and propositional standpoint logic respectively, in order to introduce ranked standpoint structures for DRSL. Moreover, we extend the non-monotonic entailment relation of rational closure from the propositional KLM case to the DRSL case. The main contribution of this paper is to characterize rational closure for DRSL both algorithmically and semantically, showing that rational closure can be characterized through a single representative ranked standpoint structure. Finally, we conclude that the semantic and algorithmic characterizations of rational closure are equivalent, and that entailment-checking for DRSL under rational closure is in the same complexity class as entailment-checking for propositional KLM.

Current and Future Challenges in Knowledge Representation and Reasoning

Knowledge Representation and Reasoning is a central, longstanding, and active area of Artificial Intelligence. Over the years it has evolved significantly; more recently it has been challenged and complemented by research in areas such as machine learning and reasoning under uncertainty. In July 2022 a Dagstuhl Perspectives workshop was held on Knowledge Representation and Reasoning. The goal of the workshop was to describe the state of the art in the field, including its relation with other areas, its shortcomings and strengths, together with recommendations for future progress. We developed this manifesto based on the presentations, panels, working groups, and discussions that took place at the Dagstuhl Workshop. It is a declaration of our views on Knowledge Representation: its origins, goals, milestones, and current foci; its relation to other disciplines, especially to Artificial Intelligence; and on its challenges, along with key priorities for the next decade.

Situated Conditional Reasoning

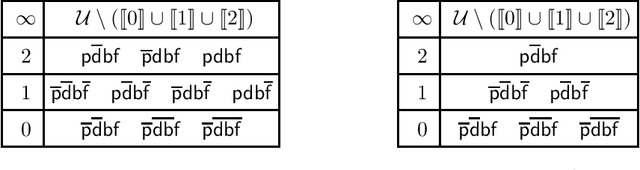
Conditionals are useful for modelling, but are not always sufficiently expressive for capturing information accurately. In this paper we make the case for a form of conditional that is situation-based. These conditionals are more expressive than classical conditionals, are general enough to be used in several application domains, and are able to distinguish, for example, between expectations and counterfactuals. Formally, they are shown to generalise the conditional setting in the style of Kraus, Lehmann, and Magidor. We show that situation-based conditionals can be described in terms of a set of rationality postulates. We then propose an intuitive semantics for these conditionals, and present a representation result which shows that our semantic construction corresponds exactly to the description in terms of postulates. With the semantics in place, we proceed to define a form of entailment for situated conditional knowledge bases, which we refer to as minimal closure. It is reminiscent of and, indeed, inspired by, the version of entailment for propositional conditional knowledge bases known as rational closure. Finally, we proceed to show that it is possible to reduce the computation of minimal closure to a series of propositional entailment and satisfiability checks. While this is also the case for rational closure, it is somewhat surprising that the result carries over to minimal closure.

Theoretical Foundations of Defeasible Description Logics

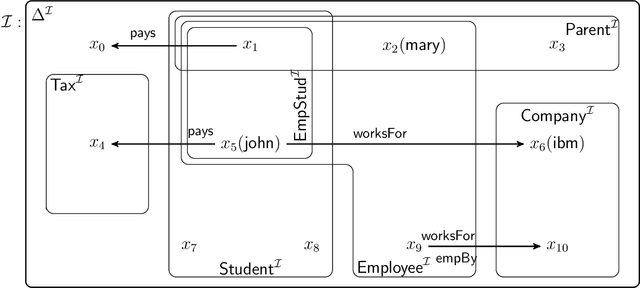
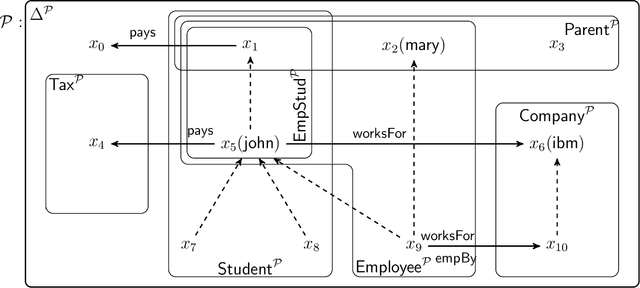
We extend description logics (DLs) with non-monotonic reasoning features. We start by investigating a notion of defeasible subsumption in the spirit of defeasible conditionals as studied by Kraus, Lehmann and Magidor in the propositional case. In particular, we consider a natural and intuitive semantics for defeasible subsumption, and investigate KLM-style syntactic properties for both preferential and rational subsumption. Our contribution includes two representation results linking our semantic constructions to the set of preferential and rational properties considered. Besides showing that our semantics is appropriate, these results pave the way for more effective decision procedures for defeasible reasoning in DLs. Indeed, we also analyse the problem of non-monotonic reasoning in DLs at the level of entailment and present an algorithm for the computation of rational closure of a defeasible ontology. Importantly, our algorithm relies completely on classical entailment and shows that the computational complexity of reasoning over defeasible ontologies is no worse than that of reasoning in the underlying classical DL ALC.

On Rational Entailment for Propositional Typicality Logic

Propositional Typicality Logic (PTL) is a recently proposed logic, obtained by enriching classical propositional logic with a typicality operator capturing the most typical (alias normal or conventional) situations in which a given sentence holds. The semantics of PTL is in terms of ranked models as studied in the well-known KLM approach to preferential reasoning and therefore KLM-style rational consequence relations can be embedded in PTL. In spite of the non-monotonic features introduced by the semantics adopted for the typicality operator, the obvious Tarskian definition of entailment for PTL remains monotonic and is therefore not appropriate in many contexts. Our first important result is an impossibility theorem showing that a set of proposed postulates that at first all seem appropriate for a notion of entailment with regard to typicality cannot be satisfied simultaneously. Closer inspection reveals that this result is best interpreted as an argument for advocating the development of more than one type of PTL entailment. In the spirit of this interpretation, we investigate three different (semantic) versions of entailment for PTL, each one based on the definition of rational closure as introduced by Lehmann and Magidor for KLM-style conditionals, and constructed using different notions of minimality.

A Polynomial Time Subsumption Algorithm for Nominal Safe $\mathcal{ELO}_\bot$ under Rational Closure

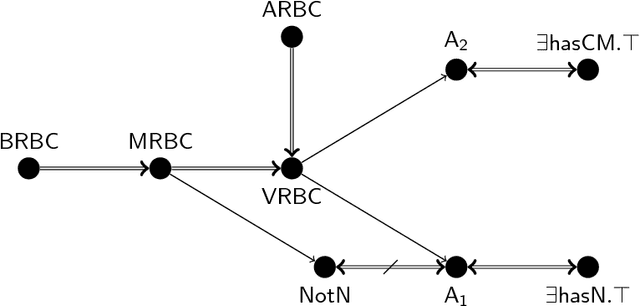
Description Logics (DLs) under Rational Closure (RC) is a well-known framework for non-monotonic reasoning in DLs. In this paper, we address the concept subsumption decision problem under RC for nominal safe $\mathcal{ELO}_\bot$, a notable and practically important DL representative of the OWL 2 profile OWL 2 EL. Our contribution here is to define a polynomial time subsumption procedure for nominal safe $\mathcal{ELO}_\bot$ under RC that relies entirely on a series of classical, monotonic $\mathcal{EL}_\bot$ subsumption tests. Therefore, any existing classical monotonic $\mathcal{EL}_\bot$ reasoner can be used as a black box to implement our method. We then also adapt the method to one of the known extensions of RC for DLs, namely Defeasible Inheritance-based DLs without losing the computational tractability.

Maximizing Expected Impact in an Agent Reputation Network -- Technical Report

Many multi-agent systems (MASs) are situated in stochastic environments. Some such systems that are based on the partially observable Markov decision process (POMDP) do not take the benevolence of other agents for granted. We propose a new POMDP-based framework which is general enough for the specification of a variety of stochastic MAS domains involving the impact of agents on each other's reputations. A unique feature of this framework is that actions are specified as either undirected (regular) or directed (towards a particular agent), and a new directed transition function is provided for modeling the effects of reputation in interactions. Assuming that an agent must maintain a good enough reputation to survive in the network, a planning algorithm is developed for an agent to select optimal actions in stochastic MASs. Preliminary evaluation is provided via an example specification and by determining the algorithm's complexity.

Imagining Probabilistic Belief Change as Imaging (Technical Report)

Imaging is a form of probabilistic belief change which could be employed for both revision and update. In this paper, we propose a new framework for probabilistic belief change based on imaging, called Expected Distance Imaging (EDI). EDI is sufficiently general to define Bayesian conditioning and other forms of imaging previously defined in the literature. We argue that, and investigate how, EDI can be used for both revision and update. EDI's definition depends crucially on a weight function whose properties are studied and whose effect on belief change operations is analysed. Finally, four EDI instantiations are proposed, two for revision and two for update, and probabilistic rationality postulates are suggested for their analysis.

Revising Incompletely Specified Convex Probabilistic Belief Bases

We propose a method for an agent to revise its incomplete probabilistic beliefs when a new piece of propositional information is observed. In this work, an agent's beliefs are represented by a set of probabilistic formulae -- a belief base. The method involves determining a representative set of 'boundary' probability distributions consistent with the current belief base, revising each of these probability distributions and then translating the revised information into a new belief base. We use a version of Lewis Imaging as the revision operation. The correctness of the approach is proved. The expressivity of the belief bases under consideration are rather restricted, but has some applications. We also discuss methods of belief base revision employing the notion of optimum entropy, and point out some of the benefits and difficulties in those methods. Both the boundary distribution method and the optimum entropy method are reasonable, yet yield different results.