Current and Future Challenges in Knowledge Representation and Reasoning

Knowledge Representation and Reasoning is a central, longstanding, and active area of Artificial Intelligence. Over the years it has evolved significantly; more recently it has been challenged and complemented by research in areas such as machine learning and reasoning under uncertainty. In July 2022 a Dagstuhl Perspectives workshop was held on Knowledge Representation and Reasoning. The goal of the workshop was to describe the state of the art in the field, including its relation with other areas, its shortcomings and strengths, together with recommendations for future progress. We developed this manifesto based on the presentations, panels, working groups, and discussions that took place at the Dagstuhl Workshop. It is a declaration of our views on Knowledge Representation: its origins, goals, milestones, and current foci; its relation to other disciplines, especially to Artificial Intelligence; and on its challenges, along with key priorities for the next decade.

Automated Aggregator -- Rewriting with the Counting Aggregate

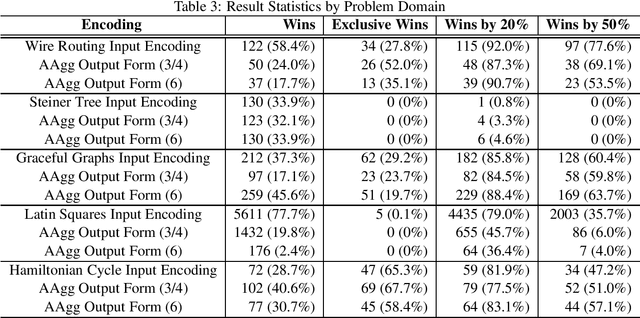
Answer set programming is a leading declarative constraint programming paradigm with wide use for complex knowledge-intensive applications. Modern answer set programming languages support many equivalent ways to model constraints and specifications in a program. However, so far answer set programming has failed to develop systematic methodologies for building representations that would uniformly lend well to automated processing. This suggests that encoding selection, in the same way as algorithm selection and portfolio solving, may be a viable direction for improving performance of answer-set solving. The necessary precondition is automating the process of generating possible alternative encodings. Here we present an automated rewriting system, the Automated Aggregator or AAgg, that given a non-ground logic program, produces a family of equivalent programs with complementary performance when run under modern answer set programming solvers. We demonstrate this behavior through experimental analysis and propose the system's use in automated answer set programming solver selection tools.

Encoding Selection for Solving Hamiltonian Cycle Problems with ASP

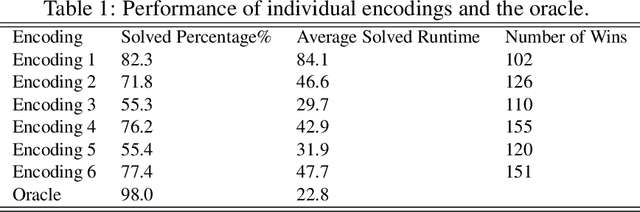
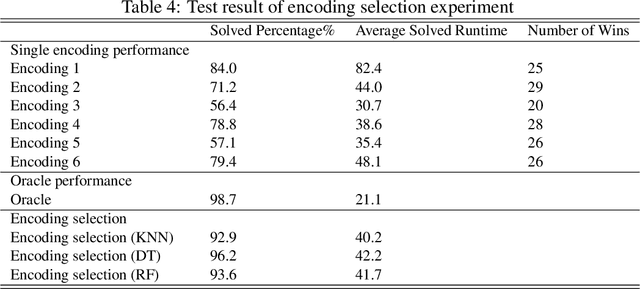
It is common for search and optimization problems to have alternative equivalent encodings in ASP. Typically none of them is uniformly better than others when evaluated on broad classes of problem instances. We claim that one can improve the solving ability of ASP by using machine learning techniques to select encodings likely to perform well on a given instance. We substantiate this claim by studying the hamiltonian cycle problem. We propose several equivalent encodings of the problem and several classes of hard instances. We build models to predict the behavior of each encoding, and then show that selecting encodings for a given instance using the learned performance predictors leads to significant performance gains.

Dual-normal Logic Programs - the Forgotten Class

Disjunctive Answer Set Programming is a powerful declarative programming paradigm with complexity beyond NP. Identifying classes of programs for which the consistency problem is in NP is of interest from the theoretical standpoint and can potentially lead to improvements in the design of answer set programming solvers. One of such classes consists of dual-normal programs, where the number of positive body atoms in proper rules is at most one. Unlike other classes of programs, dual-normal programs have received little attention so far. In this paper we study this class. We relate dual-normal programs to propositional theories and to normal programs by presenting several inter-translations. With the translation from dual-normal to normal programs at hand, we introduce the novel class of body-cycle free programs, which are in many respects dual to head-cycle free programs. We establish the expressive power of dual-normal programs in terms of SE- and UE-models, and compare them to normal programs. We also discuss the complexity of deciding whether dual-normal programs are strongly and uniformly equivalent.

Abstract Modular Systems and Solvers

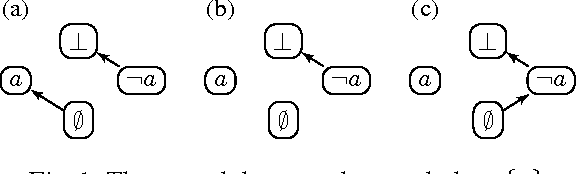
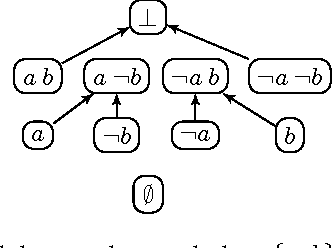
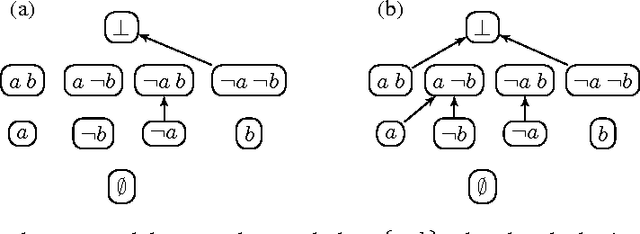
Integrating diverse formalisms into modular knowledge representation systems offers increased expressivity, modeling convenience and computational benefits. We introduce concepts of abstract modules and abstract modular systems to study general principles behind the design and analysis of model-finding programs, or solvers, for integrated heterogeneous multi-logic systems. We show how abstract modules and abstract modular systems give rise to transition systems, which are a natural and convenient representation of solvers pioneered by the SAT community. We illustrate our approach by showing how it applies to answer set programming and propositional logic, and to multi-logic systems based on these two formalisms.

The View-Update Problem for Indefinite Databases

This paper introduces and studies a declarative framework for updating views over indefinite databases. An indefinite database is a database with null values that are represented, following the standard database approach, by a single null constant. The paper formalizes views over such databases as indefinite deductive databases, and defines for them several classes of database repairs that realize view-update requests. Most notable is the class of constrained repairs. Constrained repairs change the database "minimally" and avoid making arbitrary commitments. They narrow down the space of alternative ways to fulfill the view-update request to those that are grounded, in a certain strong sense, in the database, the view and the view-update request.

Origins of Answer-Set Programming - Some Background And Two Personal Accounts

We discuss the evolution of aspects of nonmonotonic reasoning towards the computational paradigm of answer-set programming (ASP). We give a general overview of the roots of ASP and follow up with the personal perspective on research developments that helped verbalize the main principles of ASP and differentiated it from the classical logic programming.

Revisiting Epistemic Specifications

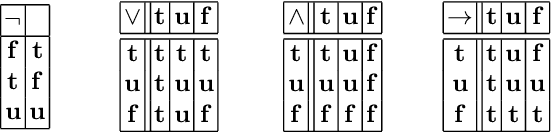
In 1991, Michael Gelfond introduced the language of epistemic specifications. The goal was to develop tools for modeling problems that require some form of meta-reasoning, that is, reasoning over multiple possible worlds. Despite their relevance to knowledge representation, epistemic specifications have received relatively little attention so far. In this paper, we revisit the formalism of epistemic specification. We offer a new definition of the formalism, propose several semantics (one of which, under syntactic restrictions we assume, turns out to be equivalent to the original semantics by Gelfond), derive some complexity results and, finally, show the effectiveness of the formalism for modeling problems requiring meta-reasoning considered recently by Faber and Woltran. All these results show that epistemic specifications deserve much more attention that has been afforded to them so far.

Reiter's Default Logic Is a Logic of Autoepistemic Reasoning And a Good One, Too

A fact apparently not observed earlier in the literature of nonmonotonic reasoning is that Reiter, in his default logic paper, did not directly formalize informal defaults. Instead, he translated a default into a certain natural language proposition and provided a formalization of the latter. A few years later, Moore noted that propositions like the one used by Reiter are fundamentally different than defaults and exhibit a certain autoepistemic nature. Thus, Reiter had developed his default logic as a formalization of autoepistemic propositions rather than of defaults. The first goal of this paper is to show that some problems of Reiter's default logic as a formal way to reason about informal defaults are directly attributable to the autoepistemic nature of default logic and to the mismatch between informal defaults and the Reiter's formal defaults, the latter being a formal expression of the autoepistemic propositions Reiter used as a representation of informal defaults. The second goal of our paper is to compare the work of Reiter and Moore. While each of them attempted to formalize autoepistemic propositions, the modes of reasoning in their respective logics were different. We revisit Moore's and Reiter's intuitions and present them from the perspective of autotheoremhood, where theories can include propositions referring to the theory's own theorems. We then discuss the formalization of this perspective in the logics of Moore and Reiter, respectively, using the unifying semantic framework for default and autoepistemic logics that we developed earlier. We argue that Reiter's default logic is a better formalization of Moore's intuitions about autoepistemic propositions than Moore's own autoepistemic logic.

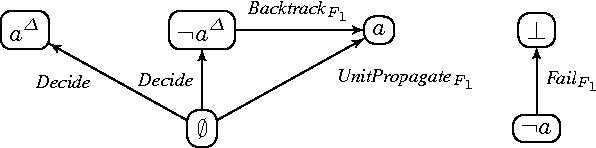
Transition Systems for Model Generators - A Unifying Approach

A fundamental task for propositional logic is to compute models of propositional formulas. Programs developed for this task are called satisfiability solvers. We show that transition systems introduced by Nieuwenhuis, Oliveras, and Tinelli to model and analyze satisfiability solvers can be adapted for solvers developed for two other propositional formalisms: logic programming under the answer-set semantics, and the logic PC(ID). We show that in each case the task of computing models can be seen as "satisfiability modulo answer-set programming," where the goal is to find a model of a theory that also is an answer set of a certain program. The unifying perspective we develop shows, in particular, that solvers CLASP and MINISATID are closely related despite being developed for different formalisms, one for answer-set programming and the latter for the logic PC(ID).