Visualizing Extensions of Argumentation Frameworks as Layered Graphs

The visualization of argumentation frameworks (AFs) is crucial for enabling a wide applicability of argumentative tools. However, their visualization is often considered only as an accompanying part of tools for computing semantics and standard graphical representations are used. We introduce a new visualization technique that draws an AF, together with an extension (as part of the input), as a 3-layer graph layout. Our technique supports the user to more easily explore the visualized AF, better understand extensions, and verify algorithms for computing semantics. To optimize the visual clarity and aesthetics of this layout, we propose to minimize edge crossings in our 3-layer drawing. We do so by an exact ILP-based approach, but also propose a fast heuristic pipeline. Via a quantitative evaluation, we show that the heuristic is feasible even for large instances, while producing at most twice as many crossings as an optimal drawing in most cases.

A Unified View on Forgetting and Strong Equivalence Notions in Answer Set Programming

Answer Set Programming (ASP) is a prominent rule-based language for knowledge representation and reasoning with roots in logic programming and non-monotonic reasoning. The aim to capture the essence of removing (ir)relevant details in ASP programs led to the investigation of different notions, from strong persistence (SP) forgetting, to faithful abstractions, and, recently, strong simplifications, where the latter two can be seen as relaxed and strengthened notions of forgetting, respectively. Although it was observed that these notions are related, especially given that they have characterizations through the semantics for strong equivalence, it remained unclear whether they can be brought together. In this work, we bridge this gap by introducing a novel relativized equivalence notion, which is a relaxation of the recent simplification notion, that is able to capture all related notions from the literature. We provide necessary and sufficient conditions for relativized simplifiability, which shows that the challenging part is for when the context programs do not contain all the atoms to remove. We then introduce an operator that combines projection and a relaxation of (SP)-forgetting to obtain the relativized simplifications. We furthermore present complexity results that complete the overall picture.

Solving Projected Model Counting by Utilizing Treewidth and its Limits

In this paper, we introduce a novel algorithm to solve projected model counting (PMC). PMC asks to count solutions of a Boolean formula with respect to a given set of projection variables, where multiple solutions that are identical when restricted to the projection variables count as only one solution. Inspired by the observation that the so-called "treewidth" is one of the most prominent structural parameters, our algorithm utilizes small treewidth of the primal graph of the input instance. More precisely, it runs in time O(2^2k+4n2) where k is the treewidth and n is the input size of the instance. In other words, we obtain that the problem PMC is fixed-parameter tractable when parameterized by treewidth. Further, we take the exponential time hypothesis (ETH) into consideration and establish lower bounds of bounded treewidth algorithms for PMC, yielding asymptotically tight runtime bounds of our algorithm. While the algorithm above serves as a first theoretical upper bound and although it might be quite appealing for small values of k, unsurprisingly a naive implementation adhering to this runtime bound suffers already from instances of relatively small width. Therefore, we turn our attention to several measures in order to resolve this issue towards exploiting treewidth in practice: We present a technique called nested dynamic programming, where different levels of abstractions of the primal graph are used to (recursively) compute and refine tree decompositions of a given instance. Finally, we provide a nested dynamic programming algorithm and an implementation that relies on database technology for PMC and a prominent special case of PMC, namely model counting (#Sat). Experiments indicate that the advancements are promising, allowing us to solve instances of treewidth upper bounds beyond 200.

Rediscovering Argumentation Principles Utilizing Collective Attacks

Argumentation Frameworks (AFs) are a key formalism in AI research. Their semantics have been investigated in terms of principles, which define characteristic properties in order to deliver guidance for analysing established and developing new semantics. Because of the simple structure of AFs, many desired properties hold almost trivially, at the same time hiding interesting concepts behind syntactic notions. We extend the principle-based approach to Argumentation Frameworks with Collective Attacks (SETAFs) and provide a comprehensive overview of common principles for their semantics. Our analysis shows that investigating principles based on decomposing the given SETAF (e.g. directionality or SCC-recursiveness) poses additional challenges in comparison to usual AFs. We introduce the notion of the reduct as well as the modularization principle for SETAFs which will prove beneficial for this kind of investigation. We then demonstrate how our findings can be utilized for incremental computation of extensions and give a novel parameterized tractability result for verifying preferred extensions.

The Effect of Preferences in Abstract Argumentation Under a Claim-Centric View

In this paper, we study the effect of preferences in abstract argumentation under a claim-centric perspective. Recent work has revealed that semantical and computational properties can change when reasoning is performed on claim-level rather than on the argument-level, while under certain natural restrictions (arguments with the same claims have the same outgoing attacks) these properties are conserved. We now investigate these effects when, in addition, preferences have to be taken into account and consider four prominent reductions to handle preferences between arguments. As we shall see, these reductions give rise to different classes of claim-augmented argumentation frameworks, and behave differently in terms of semantic properties and computational complexity. This strengthens the view that the actual choice for handling preferences has to be taken with care.

Aspartix-V21

In this solver description we present ASPARTIX-V, in its 2021 edition, which participates in the International Competition on Computational Models of Argumentation (ICCMA) 2021. ASPARTIX-V is capable of solving all classical (static) reasoning tasks part of ICCMA'21 and extends the ASPARTIX system suite by incorporation of recent ASP language constructs (e.g. conditional literals), domain heuristics within ASP, and multi-shot methods. In this light ASPARTIX-V deviates from the traditional focus of ASPARTIX on monolithic approaches (i.e., one-shot solving via a single ASP encoding) to further enhance performance.

Utilizing Treewidth for Quantitative Reasoning on Epistemic Logic Programs

Extending the popular Answer Set Programming (ASP) paradigm by introspective reasoning capacities has received increasing interest within the last years. Particular attention is given to the formalism of epistemic logic programs (ELPs) where standard rules are equipped with modal operators which allow to express conditions on literals for being known or possible, i.e., contained in all or some answer sets, respectively. ELPs thus deliver multiple collections of answer sets, known as world views. Employing ELPs for reasoning problems so far has mainly been restricted to standard decision problems (complexity analysis) and enumeration (development of systems) of world views. In this paper, we take a next step and contribute to epistemic logic programming in two ways: First, we establish quantitative reasoning for ELPs, where the acceptance of a certain set of literals depends on the number (proportion) of world views that are compatible with the set. Second, we present a novel system that is capable of efficiently solving the underlying counting problems required to answer such quantitative reasoning problems. Our system exploits the graph-based measure treewidth and works by iteratively finding and refining (graph) abstractions of an ELP program. On top of these abstractions, we apply dynamic programming that is combined with utilizing existing search-based solvers like (e)clingo for hard combinatorial subproblems that appear during solving. It turns out that our approach is competitive with existing systems that were introduced recently. This work is under consideration for acceptance in TPLP.

Expressiveness of SETAFs and Support-Free ADFs under 3-valued Semantics

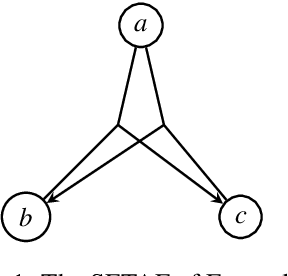
Generalizing the attack structure in argumentation frameworks (AFs) has been studied in different ways. Most prominently, the binary attack relation of Dung frameworks has been extended to the notion of collective attacks. The resulting formalism is often termed SETAFs. Another approach is provided via abstract dialectical frameworks (ADFs), where acceptance conditions specify the relation between arguments; restricting these conditions naturally allows for so-called support-free ADFs. The aim of the paper is to shed light on the relation between these two different approaches. To this end, we investigate and compare the expressiveness of SETAFs and support-free ADFs under the lens of 3-valued semantics. Our results show that it is only the presence of unsatisfiable acceptance conditions in support-free ADFs that discriminate the two approaches.

Structural Decompositions of Epistemic Logic Programs

Epistemic logic programs (ELPs) are a popular generalization of standard Answer Set Programming (ASP) providing means for reasoning over answer sets within the language. This richer formalism comes at the price of higher computational complexity reaching up to the fourth level of the polynomial hierarchy. However, in contrast to standard ASP, dedicated investigations towards tractability have not been undertaken yet. In this paper, we give first results in this direction and show that central ELP problems can be solved in linear time for ELPs exhibiting structural properties in terms of bounded treewidth. We also provide a full dynamic programming algorithm that adheres to these bounds. Finally, we show that applying treewidth to a novel dependency structure---given in terms of epistemic literals---allows to bound the number of ASP solver calls in typical ELP solving procedures.

Exploiting Database Management Systems and Treewidth for Counting

Bounded treewidth is one of the most cited combinatorial invariants, which was applied in the literature for solving several counting problems efficiently. A canonical counting problem is #SAT, which asks to count the satisfying assignments of a Boolean formula. Recent work shows that benchmarking instances for #SAT often have reasonably small treewidth. This paper deals with counting problems for instances of small treewidth. We introduce a general framework to solve counting questions based on state-of-the-art database management systems (DBMS). Our framework takes explicitly advantage of small treewidth by solving instances using dynamic programming (DP) on tree decompositions (TD). Therefore, we implement the concept of DP into a DBMS (PostgreSQL), since DP algorithms are already often given in terms of table manipulations in theory. This allows for elegant specifications of DP algorithms and the use of SQL to manipulate records and tables, which gives us a natural approach to bring DP algorithms into practice. To the best of our knowledge, we present the first approach to employ a DBMS for algorithms on TDs. A key advantage of our approach is that DBMS naturally allow to deal with huge tables with a limited amount of main memory (RAM), parallelization, as well as suspending computation.