Visualizing Extensions of Argumentation Frameworks as Layered Graphs

The visualization of argumentation frameworks (AFs) is crucial for enabling a wide applicability of argumentative tools. However, their visualization is often considered only as an accompanying part of tools for computing semantics and standard graphical representations are used. We introduce a new visualization technique that draws an AF, together with an extension (as part of the input), as a 3-layer graph layout. Our technique supports the user to more easily explore the visualized AF, better understand extensions, and verify algorithms for computing semantics. To optimize the visual clarity and aesthetics of this layout, we propose to minimize edge crossings in our 3-layer drawing. We do so by an exact ILP-based approach, but also propose a fast heuristic pipeline. Via a quantitative evaluation, we show that the heuristic is feasible even for large instances, while producing at most twice as many crossings as an optimal drawing in most cases.

Compacting Squares

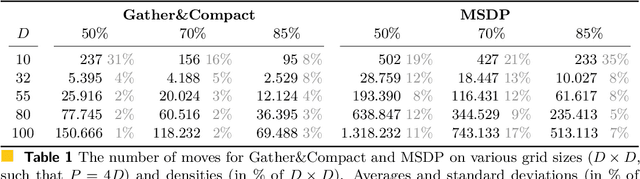
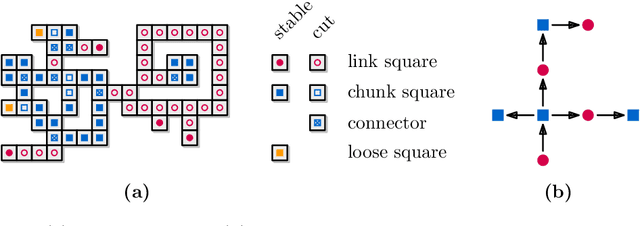
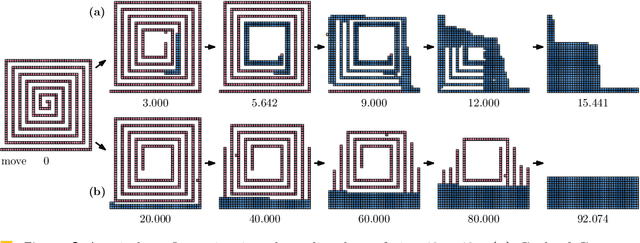
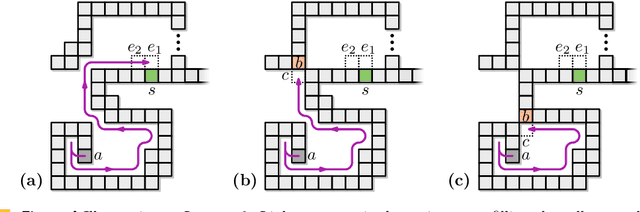
Edge-connected configurations of squares are a common model for modular robots in two dimensions. A well-established way to reconfigure such modular robots are so-called sliding moves. Dumitrescu and Pach [Graphs and Combinatorics, 2006] proved that it is always possible to reconfigure one edge-connected configuration of $n$ squares into any other using at most $O(n^2)$ sliding moves, while keeping the configuration connected at all times. For certain configurations $\Omega(n^2)$ sliding moves are necessary. However, significantly fewer moves may be sufficient. In this paper we present a novel input-sensitive in-place algorithm which requires only $O(\bar{P} n)$ sliding moves to transform one configuration into the other, where $\bar{P}$ is the maximum perimeter of the respective bounding boxes. Our Gather&Compact algorithm is built on the basic principle that well-connected components of modular robots can be transformed efficiently. Hence we iteratively increase the connectivity within a configuration, to finally arrive at a single solid $xy$-monotone component. We implemented Gather&Compact and compared it experimentally to the in-place modification by Moreno and Sacrist\'an [EuroCG 2020] of the Dumitrescu and Pach algorithm (MSDP). Our experiments show that Gather&Compact consistently outperforms MSDP by a significant margin, on all types of square configurations.