Optimal In-Place Compaction of Sliding Cubes

The sliding cubes model is a well-established theoretical framework that supports the analysis of reconfiguration algorithms for modular robots consisting of face-connected cubes. The best algorithm currently known for the reconfiguration problem, by Abel and Kominers [arXiv, 2011], uses O(n3) moves to transform any n-cube configuration into any other n-cube configuration. As is common in the literature, this algorithm reconfigures the input into an intermediate canonical shape. In this paper we present an in-place algorithm that reconfigures any n-cube configuration into a compact canonical shape using a number of moves proportional to the sum of coordinates of the input cubes. This result is asymptotically optimal. Furthermore, our algorithm directly extends to dimensions higher than three.

Better Hit the Nail on the Head than Beat around the Bush: Removing Protected Attributes with a Single Projection

Bias elimination and recent probing studies attempt to remove specific information from embedding spaces. Here it is important to remove as much of the target information as possible, while preserving any other information present. INLP is a popular recent method which removes specific information through iterative nullspace projections. Multiple iterations, however, increase the risk that information other than the target is negatively affected. We introduce two methods that find a single targeted projection: Mean Projection (MP, more efficient) and Tukey Median Projection (TMP, with theoretical guarantees). Our comparison between MP and INLP shows that (1) one MP projection removes linear separability based on the target and (2) MP has less impact on the overall space. Further analysis shows that applying random projections after MP leads to the same overall effects on the embedding space as the multiple projections of INLP. Applying one targeted (MP) projection hence is methodologically cleaner than applying multiple (INLP) projections that introduce random effects.

Characterizing Uncertainty in the Visual Text Analysis Pipeline

Current visual text analysis approaches rely on sophisticated processing pipelines. Each step of such a pipeline potentially amplifies any uncertainties from the previous step. To ensure the comprehensibility and interoperability of the results, it is of paramount importance to clearly communicate the uncertainty not only of the output but also within the pipeline. In this paper, we characterize the sources of uncertainty along the visual text analysis pipeline. Within its three phases of labeling, modeling, and analysis, we identify six sources, discuss the type of uncertainty they create, and how they propagate.

Compacting Squares

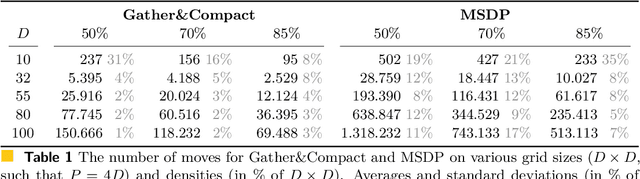
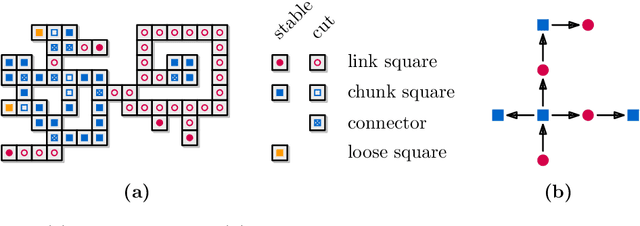
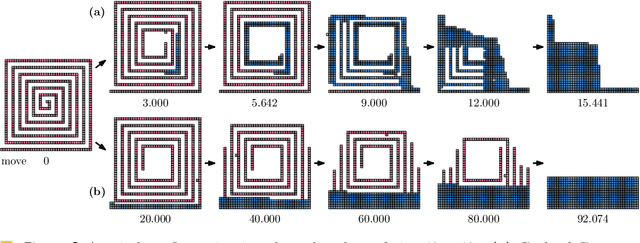
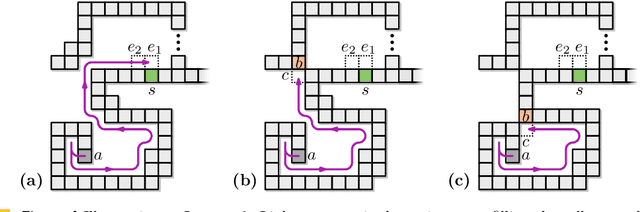
Edge-connected configurations of squares are a common model for modular robots in two dimensions. A well-established way to reconfigure such modular robots are so-called sliding moves. Dumitrescu and Pach [Graphs and Combinatorics, 2006] proved that it is always possible to reconfigure one edge-connected configuration of $n$ squares into any other using at most $O(n^2)$ sliding moves, while keeping the configuration connected at all times. For certain configurations $\Omega(n^2)$ sliding moves are necessary. However, significantly fewer moves may be sufficient. In this paper we present a novel input-sensitive in-place algorithm which requires only $O(\bar{P} n)$ sliding moves to transform one configuration into the other, where $\bar{P}$ is the maximum perimeter of the respective bounding boxes. Our Gather&Compact algorithm is built on the basic principle that well-connected components of modular robots can be transformed efficiently. Hence we iteratively increase the connectivity within a configuration, to finally arrive at a single solid $xy$-monotone component. We implemented Gather&Compact and compared it experimentally to the in-place modification by Moreno and Sacrist\'an [EuroCG 2020] of the Dumitrescu and Pach algorithm (MSDP). Our experiments show that Gather&Compact consistently outperforms MSDP by a significant margin, on all types of square configurations.