Better Hit the Nail on the Head than Beat around the Bush: Removing Protected Attributes with a Single Projection

Bias elimination and recent probing studies attempt to remove specific information from embedding spaces. Here it is important to remove as much of the target information as possible, while preserving any other information present. INLP is a popular recent method which removes specific information through iterative nullspace projections. Multiple iterations, however, increase the risk that information other than the target is negatively affected. We introduce two methods that find a single targeted projection: Mean Projection (MP, more efficient) and Tukey Median Projection (TMP, with theoretical guarantees). Our comparison between MP and INLP shows that (1) one MP projection removes linear separability based on the target and (2) MP has less impact on the overall space. Further analysis shows that applying random projections after MP leads to the same overall effects on the embedding space as the multiple projections of INLP. Applying one targeted (MP) projection hence is methodologically cleaner than applying multiple (INLP) projections that introduce random effects.

Characterizing Uncertainty in the Visual Text Analysis Pipeline

Current visual text analysis approaches rely on sophisticated processing pipelines. Each step of such a pipeline potentially amplifies any uncertainties from the previous step. To ensure the comprehensibility and interoperability of the results, it is of paramount importance to clearly communicate the uncertainty not only of the output but also within the pipeline. In this paper, we characterize the sources of uncertainty along the visual text analysis pipeline. Within its three phases of labeling, modeling, and analysis, we identify six sources, discuss the type of uncertainty they create, and how they propagate.

Obstructing Classification via Projection

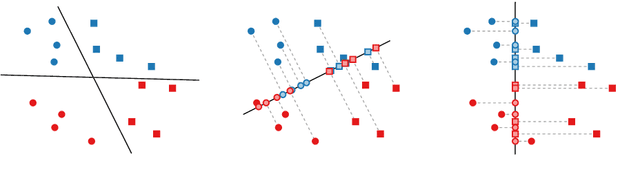
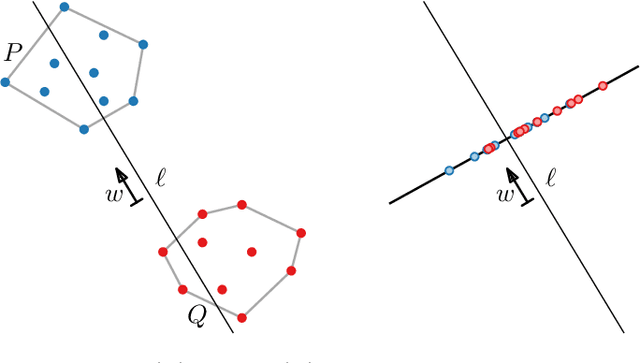
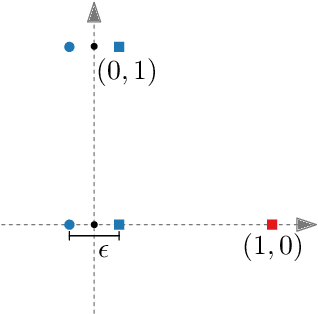
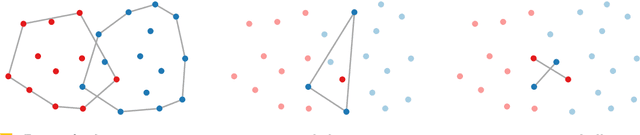
Machine learning and data mining techniques are effective tools to classify large amounts of data. But they tend to preserve any inherent bias in the data, for example, with regards to gender or race. Removing such bias from data or the learned representations is quite challenging. In this paper we study a geometric problem which models a possible approach for bias removal. Our input is a set of points P in Euclidean space R^d and each point is labeled with k binary-valued properties. A priori we assume that it is "easy" to classify the data according to each property. Our goal is to obstruct the classification according to one property by a suitable projection to a lower-dimensional Euclidean space R^m (m < d), while classification according to all other properties remains easy. What it means for classification to be easy depends on the classification model used. We first consider classification by linear separability as employed by support vector machines. We use Kirchberger's Theorem to show that, under certain conditions, a simple projection to R^(d-1) suffices to eliminate the linear separability of one of the properties whilst maintaining the linear separability of the other properties. We also study the problem of maximizing the linear "inseparability" of the chosen property. Second, we consider more complex forms of separability and prove a connection between the number of projections required to obstruct classification and the Helly-type properties of such separabilities.