Solving Projected Model Counting by Utilizing Treewidth and its Limits

In this paper, we introduce a novel algorithm to solve projected model counting (PMC). PMC asks to count solutions of a Boolean formula with respect to a given set of projection variables, where multiple solutions that are identical when restricted to the projection variables count as only one solution. Inspired by the observation that the so-called "treewidth" is one of the most prominent structural parameters, our algorithm utilizes small treewidth of the primal graph of the input instance. More precisely, it runs in time O(2^2k+4n2) where k is the treewidth and n is the input size of the instance. In other words, we obtain that the problem PMC is fixed-parameter tractable when parameterized by treewidth. Further, we take the exponential time hypothesis (ETH) into consideration and establish lower bounds of bounded treewidth algorithms for PMC, yielding asymptotically tight runtime bounds of our algorithm. While the algorithm above serves as a first theoretical upper bound and although it might be quite appealing for small values of k, unsurprisingly a naive implementation adhering to this runtime bound suffers already from instances of relatively small width. Therefore, we turn our attention to several measures in order to resolve this issue towards exploiting treewidth in practice: We present a technique called nested dynamic programming, where different levels of abstractions of the primal graph are used to (recursively) compute and refine tree decompositions of a given instance. Finally, we provide a nested dynamic programming algorithm and an implementation that relies on database technology for PMC and a prominent special case of PMC, namely model counting (#Sat). Experiments indicate that the advancements are promising, allowing us to solve instances of treewidth upper bounds beyond 200.

Determining ActionReversibility in STRIPS Using Answer Set and Epistemic Logic Programming

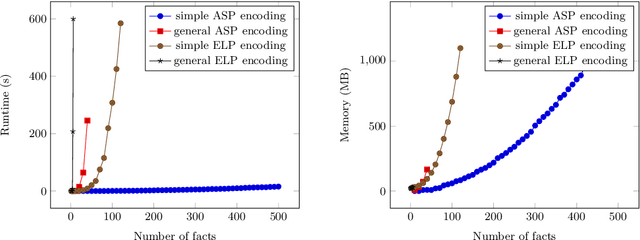
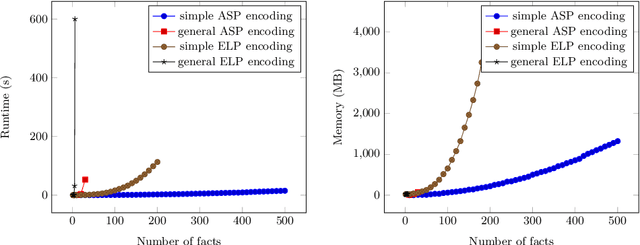
In the context of planning and reasoning about actions and change, we call an action reversible when its effects can be reverted by applying other actions, returning to the original state. Renewed interest in this area has led to several results in the context of the PDDL language, widely used for describing planning tasks. In this paper, we propose several solutions to the computational problem of deciding the reversibility of an action. In particular, we leverage an existing translation from PDDL to Answer Set Programming (ASP), and then use several different encodings to tackle the problem of action reversibility for the STRIPS fragment of PDDL. For these, we use ASP, as well as Epistemic Logic Programming (ELP), an extension of ASP with epistemic operators, and compare and contrast their strengths and weaknesses. Under consideration for acceptance in TPLP.

Structural Decompositions of Epistemic Logic Programs

Epistemic logic programs (ELPs) are a popular generalization of standard Answer Set Programming (ASP) providing means for reasoning over answer sets within the language. This richer formalism comes at the price of higher computational complexity reaching up to the fourth level of the polynomial hierarchy. However, in contrast to standard ASP, dedicated investigations towards tractability have not been undertaken yet. In this paper, we give first results in this direction and show that central ELP problems can be solved in linear time for ELPs exhibiting structural properties in terms of bounded treewidth. We also provide a full dynamic programming algorithm that adheres to these bounds. Finally, we show that applying treewidth to a novel dependency structure---given in terms of epistemic literals---allows to bound the number of ASP solver calls in typical ELP solving procedures.

selp: A Single-Shot Epistemic Logic Program Solver

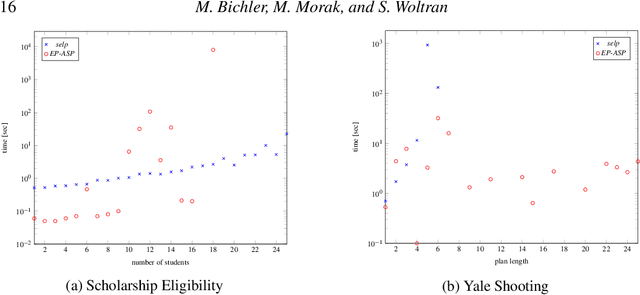
Epistemic Logic Programs (ELPs) are an extension of Answer Set Programming (ASP) with epistemic operators that allow for a form of meta-reasoning, that is, reasoning over multiple possible worlds. Existing ELP solving approaches generally rely on making multiple calls to an ASP solver in order to evaluate the ELP. However, in this paper, we show that there also exists a direct translation from ELPs into non-ground ASP with bounded arity. The resulting ASP program can thus be solved in a single shot. We then implement this encoding method, using recently proposed techniques to handle large, non-ground ASP rules, into the prototype ELP solving system "selp", which we present in this paper. This solver exhibits competitive performance on a set of ELP benchmark instances. Under consideration in Theory and Practice of Logic Programming (TPLP).

On Uniform Equivalence of Epistemic Logic Programs

Epistemic Logic Programs (ELPs) extend Answer Set Programming (ASP) with epistemic negation and have received renewed interest in recent years. This led to the development of new research and efficient solving systems for ELPs. In practice, ELPs are often written in a modular way, where each module interacts with other modules by accepting sets of facts as input, and passing on sets of facts as output. An interesting question then presents itself: under which conditions can such a module be replaced by another one without changing the outcome, for any set of input facts? This problem is known as uniform equivalence, and has been studied extensively for ASP. For ELPs, however, such an investigation is, as of yet, missing. In this paper, we therefore propose a characterization of uniform equivalence that can be directly applied to the language of state-of-the-art ELP solvers. We also investigate the computational complexity of deciding uniform equivalence for two ELPs, and show that it is on the third level of the polynomial hierarchy.

Exploiting Treewidth for Projected Model Counting and its Limits

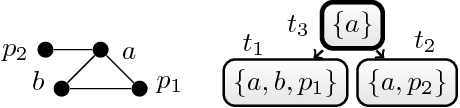
In this paper, we introduce a novel algorithm to solve projected model counting (PMC). PMC asks to count solutions of a Boolean formula with respect to a given set of projected variables, where multiple solutions that are identical when restricted to the projected variables count as only one solution. Our algorithm exploits small treewidth of the primal graph of the input instance. It runs in time $O({2^{2^{k+4}} n^2})$ where k is the treewidth and n is the input size of the instance. In other words, we obtain that the problem PMC is fixed-parameter tractable when parameterized by treewidth. Further, we take the exponential time hypothesis (ETH) into consideration and establish lower bounds of bounded treewidth algorithms for PMC, yielding asymptotically tight runtime bounds of our algorithm.

DynASP2.5: Dynamic Programming on Tree Decompositions in Action

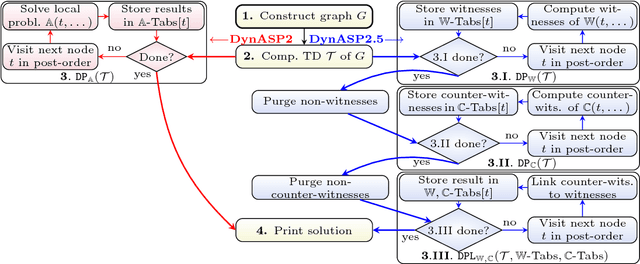
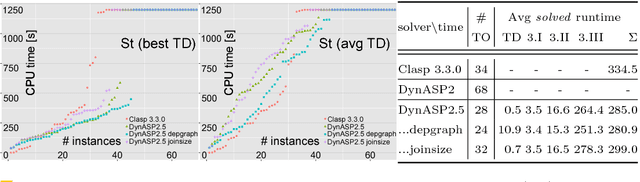
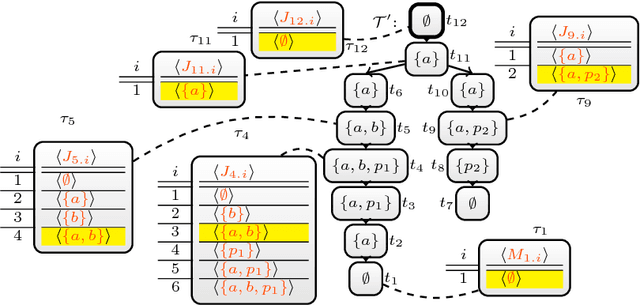
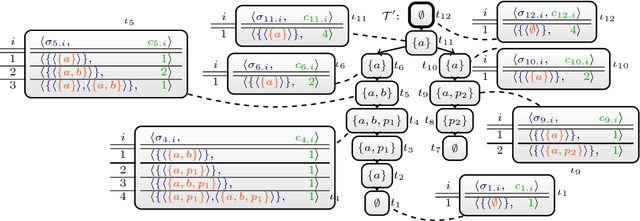
A vibrant theoretical research area are efficient exact parameterized algorithms. Very recent solving competitions such as the PACE challenge show that there is also increasing practical interest in the parameterized algorithms community. An important research question is whether dedicated parameterized exact algorithms exhibit certain practical relevance and one can even beat well-established problem solvers. We consider the logic-based declarative modeling language and problem solving framework Answer Set Programming (ASP). State-of-the-art ASP solvers rely considerably on Sat-based algorithms. An ASP solver (DynASP2), which is based on a classical dynamic programming on tree decompositions, has been published very recently. Unfortunately, DynASP2 can outperform modern ASP solvers on programs of small treewidth only if the question of interest is to count the number of solutions. In this paper, we describe underlying concepts of our new implementation (DynASP2.5) that shows competitive behavior to state-of-the-art ASP solvers even for finding just one solution when solving problems as the Steiner tree problem that have been modeled in ASP on graphs with low treewidth. Our implementation is based on a novel approach that we call multi-pass dynamic programming (M-DPSINC).

Answer Set Solving with Bounded Treewidth Revisited

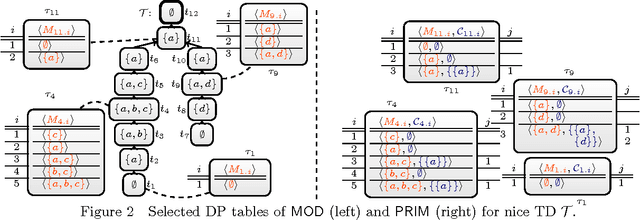
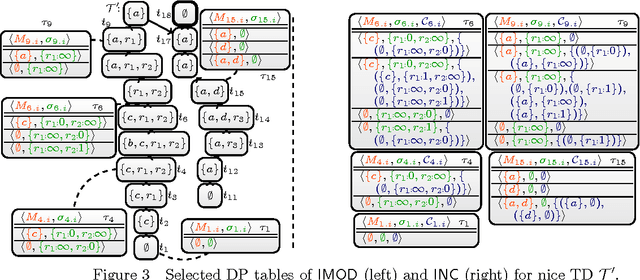
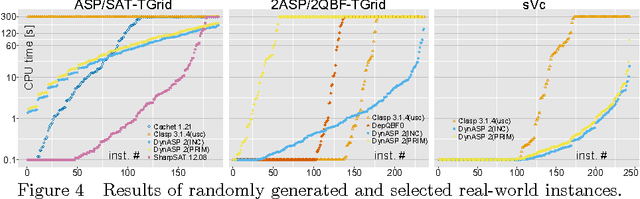
Parameterized algorithms are a way to solve hard problems more efficiently, given that a specific parameter of the input is small. In this paper, we apply this idea to the field of answer set programming (ASP). To this end, we propose two kinds of graph representations of programs to exploit their treewidth as a parameter. Treewidth roughly measures to which extent the internal structure of a program resembles a tree. Our main contribution is the design of parameterized dynamic programming algorithms, which run in linear time if the treewidth and weights of the given program are bounded. Compared to previous work, our algorithms handle the full syntax of ASP. Finally, we report on an empirical evaluation that shows good runtime behaviour for benchmark instances of low treewidth, especially for counting answer sets.

Counting Answer Sets via Dynamic Programming

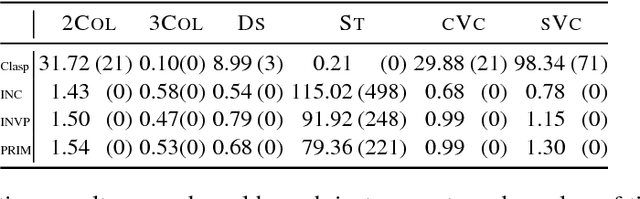
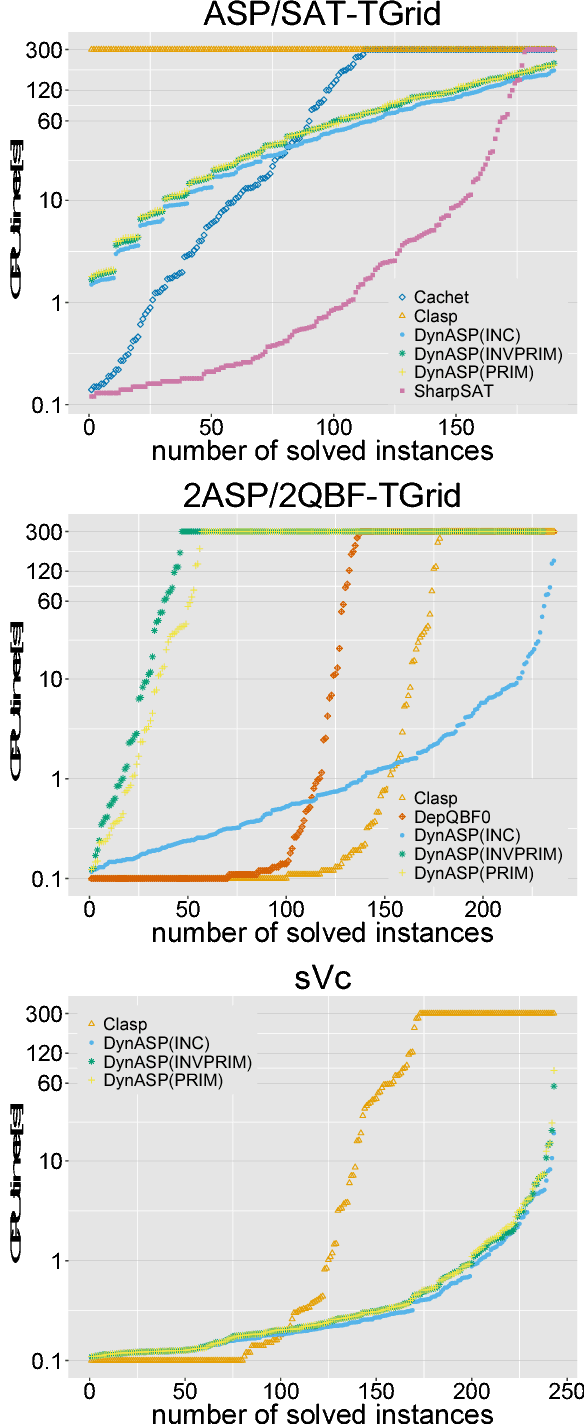
While the solution counting problem for propositional satisfiability (#SAT) has received renewed attention in recent years, this research trend has not affected other AI solving paradigms like answer set programming (ASP). Although ASP solvers are designed to enumerate all solutions, and counting can therefore be easily done, the involved materialization of all solutions is a clear bottleneck for the counting problem of ASP (#ASP). In this paper we propose dynamic programming-based #ASP algorithms that exploit the structure of the underlying (ground) ASP program. Experimental results for a prototype implementation show promise when compared to existing solvers.

lpopt: A Rule Optimization Tool for Answer Set Programming

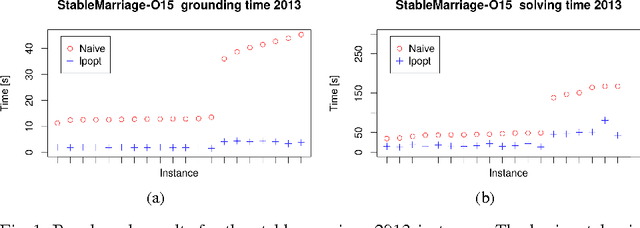
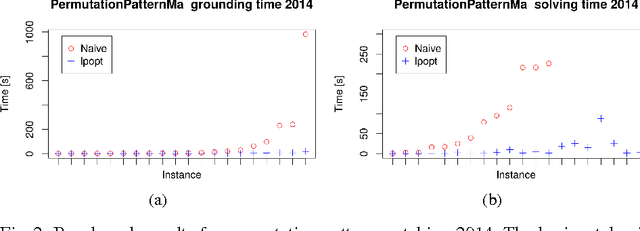
State-of-the-art answer set programming (ASP) solvers rely on a program called a grounder to convert non-ground programs containing variables into variable-free, propositional programs. The size of this grounding depends heavily on the size of the non-ground rules, and thus, reducing the size of such rules is a promising approach to improve solving performance. To this end, in this paper we announce lpopt, a tool that decomposes large logic programming rules into smaller rules that are easier to handle for current solvers. The tool is specifically tailored to handle the standard syntax of the ASP language (ASP-Core) and makes it easier for users to write efficient and intuitive ASP programs, which would otherwise often require significant hand-tuning by expert ASP engineers. It is based on an idea proposed by Morak and Woltran (2012) that we extend significantly in order to handle the full ASP syntax, including complex constructs like aggregates, weak constraints, and arithmetic expressions. We present the algorithm, the theoretical foundations on how to treat these constructs, as well as an experimental evaluation showing the viability of our approach.