DynASP2.5: Dynamic Programming on Tree Decompositions in Action
Paper and Code
Jun 28, 2017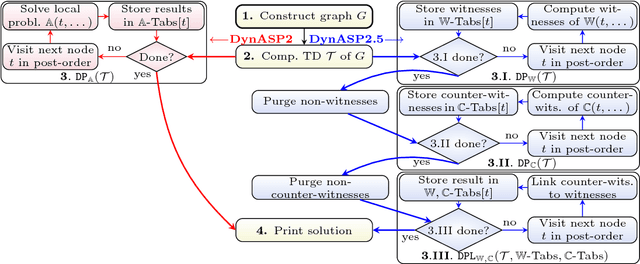


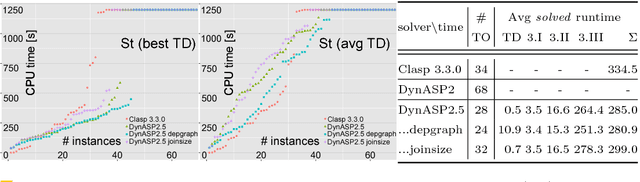
A vibrant theoretical research area are efficient exact parameterized algorithms. Very recent solving competitions such as the PACE challenge show that there is also increasing practical interest in the parameterized algorithms community. An important research question is whether dedicated parameterized exact algorithms exhibit certain practical relevance and one can even beat well-established problem solvers. We consider the logic-based declarative modeling language and problem solving framework Answer Set Programming (ASP). State-of-the-art ASP solvers rely considerably on Sat-based algorithms. An ASP solver (DynASP2), which is based on a classical dynamic programming on tree decompositions, has been published very recently. Unfortunately, DynASP2 can outperform modern ASP solvers on programs of small treewidth only if the question of interest is to count the number of solutions. In this paper, we describe underlying concepts of our new implementation (DynASP2.5) that shows competitive behavior to state-of-the-art ASP solvers even for finding just one solution when solving problems as the Steiner tree problem that have been modeled in ASP on graphs with low treewidth. Our implementation is based on a novel approach that we call multi-pass dynamic programming (M-DPSINC).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge