Manuel Bichler
selp: A Single-Shot Epistemic Logic Program Solver
Jan 04, 2020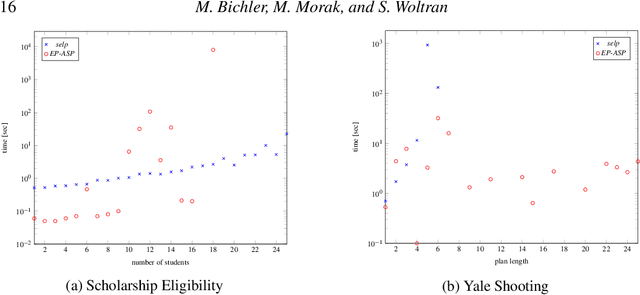
Abstract:Epistemic Logic Programs (ELPs) are an extension of Answer Set Programming (ASP) with epistemic operators that allow for a form of meta-reasoning, that is, reasoning over multiple possible worlds. Existing ELP solving approaches generally rely on making multiple calls to an ASP solver in order to evaluate the ELP. However, in this paper, we show that there also exists a direct translation from ELPs into non-ground ASP with bounded arity. The resulting ASP program can thus be solved in a single shot. We then implement this encoding method, using recently proposed techniques to handle large, non-ground ASP rules, into the prototype ELP solving system "selp", which we present in this paper. This solver exhibits competitive performance on a set of ELP benchmark instances. Under consideration in Theory and Practice of Logic Programming (TPLP).
lpopt: A Rule Optimization Tool for Answer Set Programming
Aug 23, 2016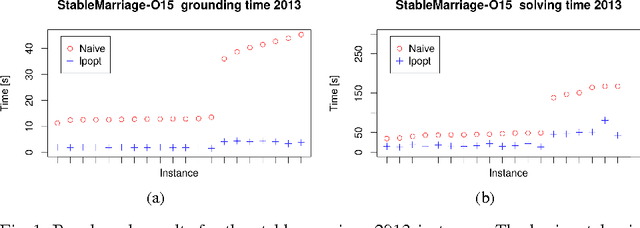
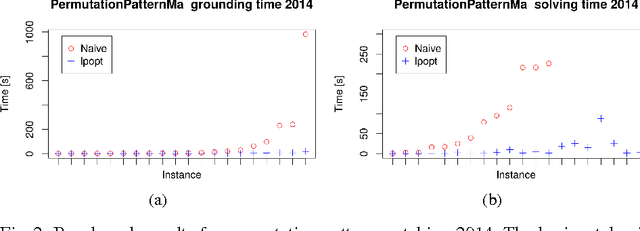
Abstract:State-of-the-art answer set programming (ASP) solvers rely on a program called a grounder to convert non-ground programs containing variables into variable-free, propositional programs. The size of this grounding depends heavily on the size of the non-ground rules, and thus, reducing the size of such rules is a promising approach to improve solving performance. To this end, in this paper we announce lpopt, a tool that decomposes large logic programming rules into smaller rules that are easier to handle for current solvers. The tool is specifically tailored to handle the standard syntax of the ASP language (ASP-Core) and makes it easier for users to write efficient and intuitive ASP programs, which would otherwise often require significant hand-tuning by expert ASP engineers. It is based on an idea proposed by Morak and Woltran (2012) that we extend significantly in order to handle the full ASP syntax, including complex constructs like aggregates, weak constraints, and arithmetic expressions. We present the algorithm, the theoretical foundations on how to treat these constructs, as well as an experimental evaluation showing the viability of our approach.
The Power of Non-Ground Rules in Answer Set Programming
Aug 05, 2016
Abstract:Answer set programming (ASP) is a well-established logic programming language that offers an intuitive, declarative syntax for problem solving. In its traditional application, a fixed ASP program for a given problem is designed and the actual instance of the problem is fed into the program as a set of facts. This approach typically results in programs with comparably short and simple rules. However, as is known from complexity analysis, such an approach limits the expressive power of ASP; in fact, an entire NP-check can be encoded into a single large rule body of bounded arity that performs both a guess and a check within the same rule. Here, we propose a novel paradigm for encoding hard problems in ASP by making explicit use of large rules which depend on the actual instance of the problem. We illustrate how this new encoding paradigm can be used, providing examples of problems from the first, second, and even third level of the polynomial hierarchy. As state-of-the-art solvers are tuned towards short rules, rule decomposition is a key technique in the practical realization of our approach. We also provide some preliminary benchmarks which indicate that giving up the convenient way of specifying a fixed program can lead to a significant speed-up. This paper is under consideration for acceptance into TPLP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge