Exploiting Treewidth for Projected Model Counting and its Limits
Paper and Code
May 14, 2018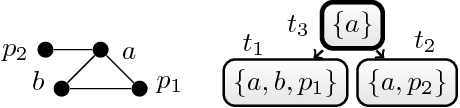
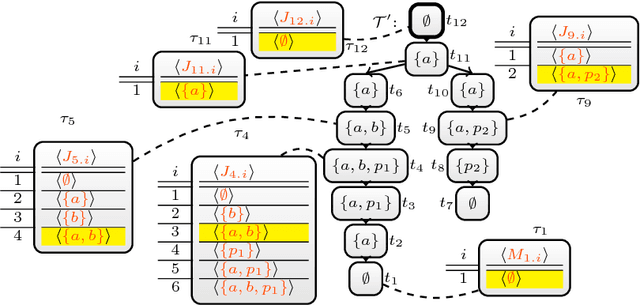
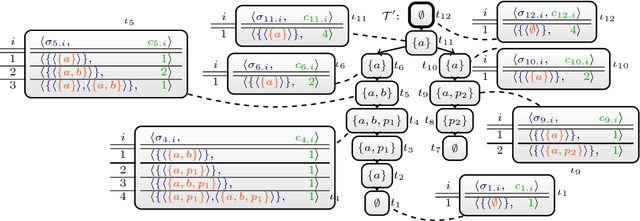
In this paper, we introduce a novel algorithm to solve projected model counting (PMC). PMC asks to count solutions of a Boolean formula with respect to a given set of projected variables, where multiple solutions that are identical when restricted to the projected variables count as only one solution. Our algorithm exploits small treewidth of the primal graph of the input instance. It runs in time $O({2^{2^{k+4}} n^2})$ where k is the treewidth and n is the input size of the instance. In other words, we obtain that the problem PMC is fixed-parameter tractable when parameterized by treewidth. Further, we take the exponential time hypothesis (ETH) into consideration and establish lower bounds of bounded treewidth algorithms for PMC, yielding asymptotically tight runtime bounds of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge